Алгебра. 9-а и 9-б классы. 17.04.2020.
Тема урока: Сочетание
Цели: ввести понятие сочетания из п элементов по k (k ≤ п); вывести формулу нахождения числа сочетаний из п элементов по k; формировать умения решать комбинаторные задачи с применением данной формулы.
Ход урока
I. Организационный момент.
II. Устная работа.
1. З а д а ч а. В футбольном турнире участвуют несколько команд. Оказалось, что все они для трусов и футболок использовали белый, красный, синий, зеленый или желтый цвета, причем были представлены все возможные варианты.
а) Сколько команд участвовали в турнире?
б) Сколько команд играли в зеленых футболках?
в) У скольких команд футболки и трусы были разного цвета?
г) У скольких команд футболки и трусы были разного цвета, причем трусы были не красные?
2. Найти значение выражения:
а) Р 4 + Р 3; б) Р 6 – Р 5; в) 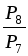 ; г)
; г) 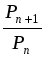 ;
;
д) 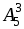 ; е)
; е) 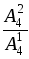 ; ж)
; ж) 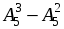 ; з)
; з) 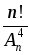 . Записать в тетрадях.
. Записать в тетрадях.
III. Объяснение нового материала.
1. Объяснение нового материала целесообразно начать с решения практической задачи:
«Сколькими способами можно смешать по три краски из имеющихся пяти?».
Р е ш е н и е
Обозначим имеющиеся краски буквами латинского алфавита a, b, c, d, e. Выпишем возможные варианты смешивания красок, учитывая, что от порядка расположения красок результат не зависит:
abc, abd, abe, ace, ade
bcd, bce, bde
cde
Мы указали различные способы смешивания красок, в которых по-разному сочетаются три краски из данных пяти. Говорят, что мы составили все возможные сочетания из 5 элементов по 3.
2. Определение. Сочетанием из п элементов по k называют любое множество, составленное из k элементов, выбранных из данных п элементов.
П о д ч е р к и в а е м, что, в отличие от размещений, в сочетаниях не имеет значения, в каком порядке указаны элементы. Два сочетания из п элементов по k отличаются друг от друга хотя бы одним элементом.
3. Обозначение. 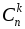 (читается «С из п по k »).
(читается «С из п по k »).
В рассмотренном примере мы нашли, что 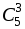 = 10.
= 10.
4. Вывод формулы числа сочетаний из п по k, где k ≤ п.
В отличие от предыдущих тем, при доказательстве мы опираемся не напрямую на комбинаторное правило умножения, а на ранее выведенные формулы числа перестановок и размещений.
Сперва замечаем, что 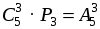 (по комбинаторному правилу умножения), значит,
(по комбинаторному правилу умножения), значит, 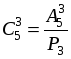 .
.
И затем проводим аналогичные рассуждения для общего случая:
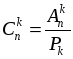
Учитывая, что 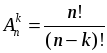 , где п ≤ k, получаем, что
, где п ≤ k, получаем, что
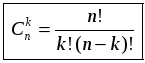
| – формула вычисления числа сочетаний из п по k, где k ≤ п. |
5. Рассматриваем примеры задач на нахождение числа сочетаний из учебника на с. 184–185.
IV. Формирование умений и навыков.
Рассматриваем задачи на применение формулы нахождения числа сочетаний из п по k. Для предотвращения формального применения формулы требуем обоснования ее выбора.
Упражнения:
№ 768.
Р е ш е н и е
Выбираем 2 учащихся из 7, порядок выбора не имеет значения (оба выбранных пойдут на олимпиаду как полностью равноправные); количество способов выбора равно числу сочетаний из 7 по 2:
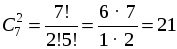 .
.
О т в е т: 21 способ.
№ 770.
Р е ш е н и е
Выбор 6 из 10 без учета порядка:
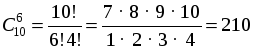 .
.
О т в е т: 210 способов.
№ 772.
Р е ш е н и е
Из 11 человек 5 должны поехать в командировку:
а) Заведующий едет, нужно выбрать еще 4 из 10 оставшихся:
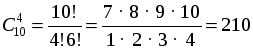
б) Заведующий остается, нужно выбрать 5 из 10 сотрудников:
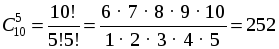
О т в е т: а) 210 способов; б) 252 способа.
Следующие три задачи – повышенной сложности.
№ 773.
Р е ш е н и е
а) Словарь выбирается, нужно выбрать еще 2 книги из 11:
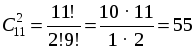 .
.
б) Словарь не выбирается, выбираем 3 книги из 11:
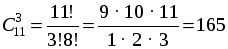 .
.
О т в е т: а) 55 способов; б) 165 способов.
№ 774. При решении используется не только формула числа сочетаний, но и комбинаторное правило умножения.
Р е ш е н и е
Сперва выбираем 4 маляров из 12:
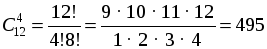 способов.
способов.
Затем выбираем 2 плотников из 5:
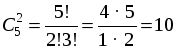 способов.
способов.
Каждый из способов выбора маляров можно скомбинировать с каждым выбором плотников, следовательно, всего способов (по комбинаторному правилу умножения): 495 · 10 = 4950.
О т в е т: 4950 способов.
№ 775.
Р е ш е н и е
Нужно сделать два выбора: 3 книги из 10 (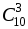 способов) и 2 журнала из 4 (
способов) и 2 журнала из 4 (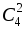 способов) – порядок выбора значения не имеет. Каждый выбор книг может сочетаться с каждым выбором журналов, поэтому общее число способов выбора по правилу произведения равно:
способов) – порядок выбора значения не имеет. Каждый выбор книг может сочетаться с каждым выбором журналов, поэтому общее число способов выбора по правилу произведения равно:
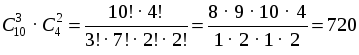
О т в е т: 720 способов.
V. Итоги урока.
В о п р о с ы у ч а щ и м с я:
– Что называется сочетанием из п элементов по k?
– Запишите формулу вычисления числа сочетаний из п элементов по k.
– В чем отличие сочетания из п элементов по k от размещения из п элементов по k.
Домашнее задание: прочитать п.33, выполнить № 769, № 771, № 783.
З а д а ч а. В классе учатся 16 мальчиков и 12 девочек. Для уборки территории требуется выделить четырех мальчиков и трех девочек. Сколькими способами это можно сделать?