Релевантность R определяется как отношение:
· – вероятности того, что d – релевантный и не релевантный соответственно
Допущения:
· Структура документа описывается бинарным вектором в пространстве терминов
· Релевантность документа запросу оценивается независимо от других документов.
Вероятностные модели: правило принятия решения
· Вероятность вычисляется на основе теоремы Байеса:
· P(R) – вероятность того, что случайно выбранный из коллекции документ D является релевантным
· P(d|R) – вероятность случайного выбора документа d из множества релевантных документов
· P(d) – вероятность случайного выбора документа d из коллекции D
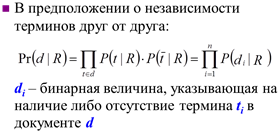
Вероятностные модели: правило принятия решения
константа, не зависящая от документов
ci – вес релевантности термина, показывающий дискриминантную способность между релевантными и нерелевантными документами термина ti.
Проблема: оценка вероятностей pt и qt
Вероятностные модели: достоинства и недостатки
Достоинства:
· Хорошее теоретическое обоснование
· При имеющейся информации дают наилучшие предсказания релевантности
· Могут быть реализованы аналогично векторным моделям
Недостатки:
· Требуется информация о релевантности или ее приближенные оценки
· Структура документа описывается только терминами
· Оптимальные результаты получаются только в процессе обучения на основе информации о релевантности
Матричная модель
Рассматривает множество из n документов.
На его основе можно построить множество из m терминов, которые хоть раз встречались в каком-либо или более документах.
Можно ввести матрицы сопряженности трех типов:
o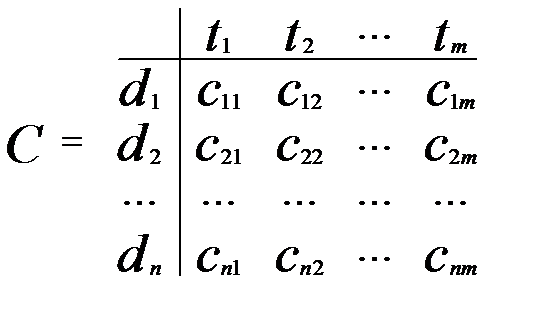 
“документ-документ”
|
|
o “термин-термин”
o “документ-термин”
Элемент d [i,j] указывает на наличие терминов содержащихся одновременно в j -м и i -м документах (бинарный случай), либо равен количеству общих терминов в этих документах
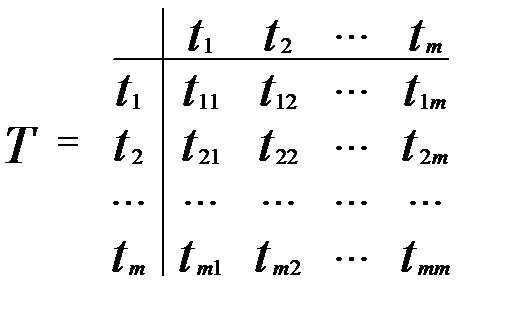
Элемент t[i,j] указывает на наличие документов содержащих одновременно j -й и i -й термины (бинарный случай), либо равен количеству таких документов
Запрос пользователя можно представить в виде:
· n -мерного вектора-строки Q [ qi ], i -ая координата которого не равна нулю в том случае, если i -ый документ включен пользователем в список документов, представляющих его запрос
· m -мерного вектора-столбца Q [ qi ], i -ая координата которого равна единице, если i -ый термин включен пользователем в список терминов, представляющий его запрос.
Реакция системы (вектор релевантностей) на запрос пользователя Q вычисляется как:
· A = C * Q
· Значение i -ой координаты n -мерного вектора A [ ai ] при этом оказывается равным числу терминов запроса (бинарный случай), оказавшихся в i -ом документе.
Информационный поиск описывается в виде итерационного процесса:
A(0) = C*Q(0)
Q(1) = CT*A(0)
A(1) = C*Q(1)
A(t) = C*Q(t)
Q(t+1) = CT*A(t)
Элементы Q(i), i>0, рассматриваются как уточненные величины значимостей терминов в запросе.
Можно заметить, что
Q(t) = (CTС)tQ(0)
A(t) = (CCT)t*A(0)
Из теоремы Сильвестра при достаточно больших t можно получить приближение:
Q(t+1) = λ0Q(t)
A(t+1) = λ0A(t)
где λ0 – собственное значение матрицы CTС.
Видно, что с увеличением t векторы Q(t) и A(t) стремятся принимать направления собственных векторов матриц CTС и СCT, соответствующих собственным значениям этих матриц. Т.е. если вектор Q(0) не учитывает фактор поисковой среды, то уже начиная с Q(1) этот фактор учитывается. При больших значениях t вектор Q(t) выражает только свойства самой среды.
|
|
Вывод: на первых тактах (при небольших t) итерационный процесс улучшает качество поиска, но при дальнейших итерациях качество поиска ухудшается, поскольку результаты перестают зависеть от запроса пользователя.
Корректировка модели:
A(0) = C*Q(0)
Q(1) = CT*A(0) + Q(0)
A(1) = C*Q(1)
……………………..
A(t) = C*Q(t)
Q(t+1) = CT*A(t) + Q(0)
Можно показать, что при достаточно больших значениях t матрицы Q и A являются решением системы уравнений:
A = CQ
Q = CTA+Q(0)
Лекция 6