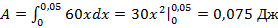Тема: Приложение определенных интегралов
Определенный интеграл широко используется при вычислениях различных геометрических и физических величин: вычисление площади плоских фигур, вычисление объемов тел вращения, вычисление длины дуги, вычисление пути, пройденного телом, вычисление работы силы.
I. Вычисление площадей плоских фигур.
Фигура, ограниченная кривой y = f(x), осью 0х, прямыми х = а, х = в называется криволинейной трапецией.
| Расположение графиков функций на координатной плоскости | Формула для вычисления площади | ||
| 1) | Криволинейная трапеция ограничена осью Ох и лежит над ней. |
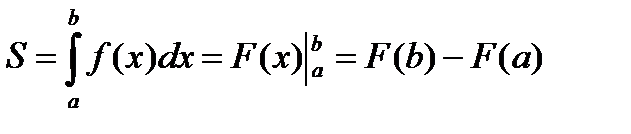
| |
| 2) | Криволинейная трапеция ограничена осью Ох и лежит под ней. |
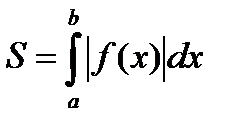
| |
| 3) |
Фигура ограничена двумя кривыми 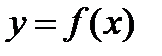 и и 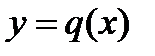
|
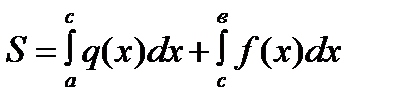
| |
| 4) | Фигура не ограничена осью Ох | 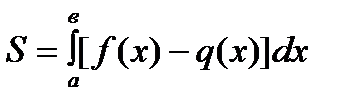
|
№1. Используя данные из таблицы, для каждого рисунка напишите формулу, по которой вычисляется площадь заштрихованной фигуры.
1) 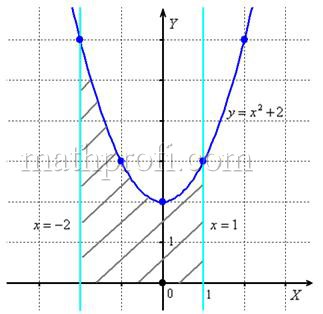 2)
2) 3)
4)
Алгоритм нахождения площади фигуры:
1. Построить на одной координатной плоскости графики данных функций.
2. Заштриховать фигуру, ограниченную построенными линиями.
3. Найти точки, ограничивающие фигуру справа и слева.
4. Найти площадь фигуры по соответствующей формуле.
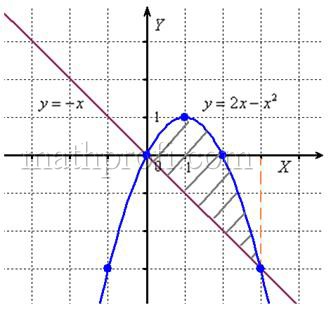
Пример 1. Найти площадь фигуры, ограниченную линиями: 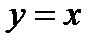 и
и 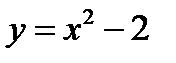
Решение: Построим графики данных функций
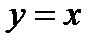 - прямая
- прямая
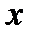
| -1 | ||
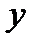
| -1 |
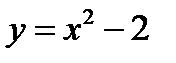 - парабола, ветви вверх
- парабола, ветви вверх
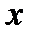
| -1 | -2 | |||
| -2 | -1 | -1 |
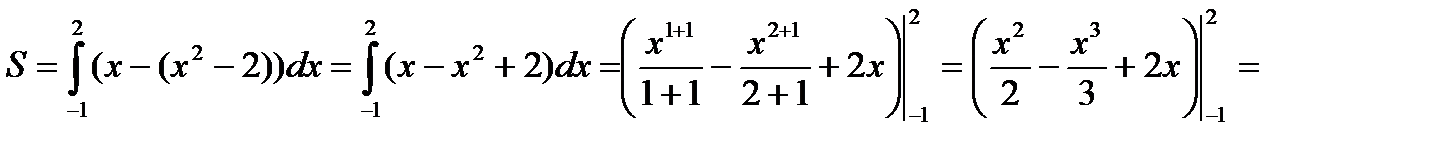
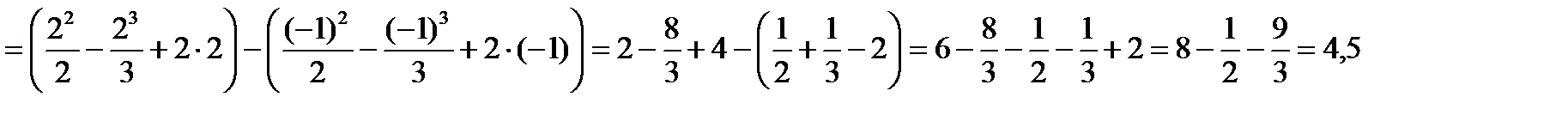
№2. Найти площадь фигуры, ограниченную линиями: 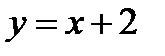 и
и 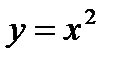
II. Применение определенного интеграла при решении физических и технических задач.
1. Задача о вычислении пути.
Пусть материальная точка движется прямолинейно с некоторой мгновенной скорость v = v(t). Требуется найти путь, который пройдет тело за промежуток времени от t = T1 до t = T2.
В простейшем случае, если мгновенная скорость постоянна, то путь, пройденный телом равен (по определению, известном из курса физики) произведению скорости на время движения: 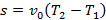 . В общем случае, когда мгновенная скорость не постоянна, её вычисляют по формуле:
. В общем случае, когда мгновенная скорость не постоянна, её вычисляют по формуле: 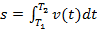
Пример 2: Тело движется прямолинейно со скоростью 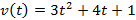 м/с. Найти путь, пройденный телом за первые 3 сек.
м/с. Найти путь, пройденный телом за первые 3 сек.
Решение: по формуле получим 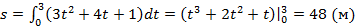
Пример 3: Точка движется прямолинейно со скоростью v(t) = at + v0 . Какой путь пройдет точка за промежуток времени от t = T1 до t = T2 ?
Решение: По формуле получим 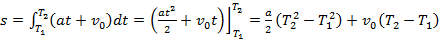
Пример 4: Тело движется прямолинейно со скоростью 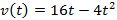 . Найти длину пути от начала движения до его остановки.
. Найти длину пути от начала движения до его остановки.
Решение: Скорость тела в момент начала его движения и остановки равна 0. Найдем момент остановки тела. Приравняв для этого его скорость к нулю и решив уравнение, получим: 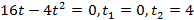 .
.
Далее, по формуле имеем: 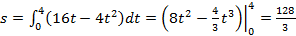
Задача о силе давления жидкости.
Пусть пластинка в виде криволинейной трапеции погружена вертикально в жидкость с плотностью ρ так, что ее боковые стороны параллельны поверхности жидкости и находятся ниже ее уровня соответственно на расстоянии a и b (рис.1)
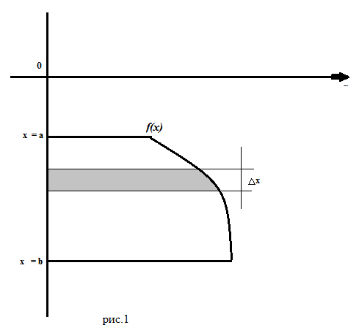
Сила давления жидкости на пластинку вычисляется по формуле: 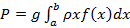
Пример 5: Аквариум имеет форму прямоугольного параллелепипеда. Найти силу давления воды (плотность воды 1000 кг/м2), наполняющей аквариум, на одну из его вертикальных стенок, размеры которой 0,4 м на 0,7 м
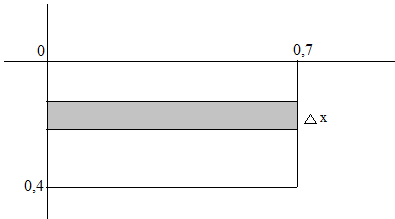
Решение: Для нахождения силы давления воспользуемся формулой. Стенка имеет форму прямоугольника, поэтому f(x) = 0,7, 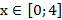 ,
,
получаем: 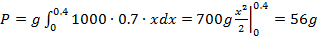 .
.
Учитывая, что 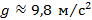 , имеем
, имеем 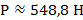 .
.
Работа переменной силы.
Пусть материальная точка движется под действием силы F по прямой. Проекция этой силы на ось Ох есть функция от х. Будем обозначать ее через f(x) и предполагать, что f есть непрерывная функция. Пусть под действием силы F материальная точка переместилась из точки М(а) в точку M(b). Работа переменной силы вычисляется по формуле: 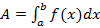
Пример 6: Сила упругости пружины, растянутой на 0,05 м, равна 3 Н. Какую работу надо произвести, чтобы растянуть пружину на эти 0,05м?
Решение: По закону Гука сила F, растягивающая или сжимающая пружину, пропорциональна этому растяжению или сжатию, т.е.  , где х – величина растяжения или сжатия, k – коэффициент пропорциональности. Из условия следует, что
, где х – величина растяжения или сжатия, k – коэффициент пропорциональности. Из условия следует, что 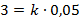 , т.е. k = 60, следовательно, F = 60x.
, т.е. k = 60, следовательно, F = 60x.
Используя формулу, получим: