Определение. Внутренней энергией какого-либо тела называется энергия этого тела за вычетом кинетической энергии тела как целого и потенциальной энергии тела во внешнем поле сил. Она является функцией внутреннего состояния системы. Для идеального газа внутренняя энергия состоит из суммы энергий поступательного, вращательного и колебательного движений молекул. (Заметим, что в общем случае во внутреннюю энергию входят энергия взаимодействия атомов, энергия электронных оболочек, внутриядерная энергия и др.). Внутреннюю энергию одного моля идеального газа найдём, умножив число Авогадро на среднюю энергию одной молекулы:
Учитывая, что 
, получим:
|
т.е. внутренняя энергия идеального газа является функцией температурыи пропорциональна ей, а также зависит от числа степеней свободы молекул. То, что внутренняя энергия является функцией состояния системы, означает, что всякий раз, когда система оказывается в данном состоянии, ее внутренняя энергия принимает присущее этому состоянию значение, независимо от предыстории системы. Следовательно, изменение внутренней энергии при переходе системы из одного состояния в другое будет всегда равно разности значений внутренней энергии в этих состояниях, независимо от пути, по которому совершался переход.
Свяжем внутреннюю энергию с теплоёмкостью. По определению теплоёмкость в процессе при постоянном объёме 
, для идеального газа
|
Соответственно
|
3. Основное уравнение молекулярно-кинетической теории.
Постановка задачи. Требуется получить связь между макропараметрами – давлением P, температурой T, с микропараметрами – массой молекулы m, её скоростью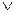 
и концентрацией молекул n.
|
|
Пусть имеется некоторый сосуд с газом. Будем считать, что молекулы могут двигаться вдоль осей x, y, z. Выберем на стенке сосуда участок поверхности 
(Рис. 7.2). Если в сосуде N молекул, то вследствие равновероятности этих направлений вдоль каждой оси будет двигаться 
| молекул. Половина из них движется вдоль данного направления, т.е.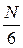 
(ось имеет два направления).
Предположим, что все молекулы движутся с одинаковой скоростью, равной  . Тогда за время  до элемента стенки долетят молекулы, заключённые в объёме параллелепипеда с основанием и высотой . Число этих молекул равно
|
| Рис. 7.2 |
произведению плотности молекул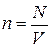 
(где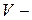 
объём сосуда) на объём 
, т.е. число молекул, летящих к площади
(1)
По закону сохранения импульса каждая молекула при ударе о стенку передаёт ей импульс (удар считается упругим), равный изменению импульса молекулы (Рис. 7.3, а, б).
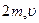. (2)
По 2-му закону Ньютона:
, (3)
где 
сила, действующая со стороны молекулы на стенку; 
длительность взаимодействия молекулы со стенкой.
Для всех молекул, находящихся в параллелепипеде:
|  , где
 средняя сила, с которой молекулы действуют на стенку . Учитывая соотношение (3):
 ,
подставляя (1) и (2) в последнее соотношение, получим:
| ||||
| рис. 7.3 |
.
Поделив правую и левую части на , учитывая, что
по определению давления 
и производя необходимые сокращения, получим 
или 
.
Если в выводе учесть, что скорости отдельных молекул могут быть различными, то величину 
следует заменить средней величиной квадрата скорости 
.
А так как средняя энергия поступательного движения молекулы
|
|
,
то
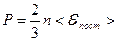
| Основное уравнение молекулярно-кинетической теории. |
Физический смысл уравнения: давление, оказываемое газом на стенки сосуда прямо пропорциональна числу молекул в единице объёма и средней кинетической энергии поступательного движения одной молекулы.
4. Уравнение состояния идеального газа Клапейрона-Менделеева
(Клапейрон (1799 – 1864) – французский физик и инженер; Менделеев Дмитрий Иванович (1834 – 1907) – великий русский учёный). Опыт даёт, что при небольших плотностях газы подчиняются уравнению (Клапейрона):
.
В соответствии с законом Авогадро моли всех газов занимают при одинаковых условиях одинаковый объём.
Отсюда const будет одинакова для всех газов, если количество равно 1 молю. Обозначив const=R, получим (Менделеев):
Уравнение состояния идеального газа для одного моля, где газовая постоянная 
, а 
- объем 1 моля газа.
|
Если у нас имеется 
молей, то объём будет 
, 
, подставим в уравнение состояния для 1-го моля:
или 
.
Количество вещества можно представить в виде отношения массы газа m к молярной массе газа М 
и окончательно уравнение состояния идеального газа (уравнение Клапейрона-Менделеева) для массы газа m:
(4)
Следствие из уравнения Клапейрона-Менделеева. Газовую постоянную выразим как 
. Произведение 
, тогда 
. Разделим обе части последнего уравнения на V и, учитывая, что
концентрация молекул, получим
(5)
Оба уравнения (4) и (5) представляют различные формы записи уравнения состояния идеального газа. Это уравнение позволяет достаточно просто оценить параметры газа, если его можно считать идеальным.
|
|
Вопросы для самоконтроля.
1. Какой газ называется идеальным? Опишите модель идеального газа.
2. Что называется числом степеней свободы механической системы i?
3. Чему равно число i для одноатомной и многоатомной молекул? Обоснуйте свой ответ.
4. Что утверждает закон равнораспределения?
5. Как зависит внутренняя энергия идеального газа от его абсолютной температуры?
6. Как объясняют давление газа в МКТ?
7. Запишите основное уравнение молекулярно-кинетической теории. Что называют микро- и макропараметрами системы?
8. Проделайте вывод основного уравнения МКТ.
9. Что позволяет рассчитать уравнение состояния идеального газа Клапейрона-Менделеева?
Лекция №8