Средние скорости молекул

Найдём наиболее вероятную скорость, соответствующую максимумуфункции распределения. Эта скорость определяется из условия

, т.е.

Проведя дифференцирование произведения функций, получим

Средняя скорость молекул (имеется в виду средняя арифметическая скорость) по определению из формулы статического усреднения

Средняя скорость входит в коэффициенты диффузии, вязкости, теплопроводности и, соответственно используется в расчётах этих процессов.

Среднеквадратичная скорость ;

, откуда

Эта скорость входит в основное уравнение молекулярно-кинетической теории. Качественно положение характерных (средних) скоростей показано на рис. 8.6

		Проанализируем, как будет меняться ход кривой при изменении температуры газа. При увеличении температуры (или уменьшении массы молекулы) максимум кривой смещается вправо (из ) и становится ниже (площадь под кривой остаётся неизменной) (Рис. 8.7)
	Рис. 8.6
Рис. 8.7

3. Барометрическая формула.

Атмосферное давление на высоте h обусловлено весом вышележащих слоёв газа. Давление на высоте h+dh будет P+dP (dh>0, dP<0, т.к. вес и давление с высотой убывают).

Разность давлений P и P+dP обусловлена весом газа, заключённого в объёме цилиндра, с площадью основания, равной и высотой dh (Рис. 8.8).

	, где – плотность газа на высоте , отсюда (*) При нормальных условиях воздух можно считать идеальным газом. Тогда можно найти из уравнения состояния идеального газа , здесь
Рис. 8.8

М – средняя масса моля воздуха. Плотность , подставим в (*), получим

. Поделим обе части на Р: . Возьмём интеграл от левой и правой частей:

.

Предел давление на уровне h =0. Для случая, когда температура постоянная (изотермическая атмосфера), интегрируя, получим:

, отсюда получаем барометрическую формулу.

	Графическая иллюстрация этой формулы на рис. 8.9 Давление убывает с высотой тем быстрее, чем тяжелее газ и чем ниже температура.
Рис. 8.9

Распределение Больцмана

В барометрической формуле в отношении M/R разделим и числитель и знаменатель на число Авогадро .

, где

масса одной молекулы,

постоянная Больцмана.

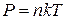
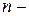Вместо Р и подставим соответственно. (см. лекцию №7), где плотность молекул на высоте h, плотность молекул на высоте .

Из барометрической формулы в результате подстановок и сокращений получим распределение концентрации молекул по высоте в поле силы тяжести Земли.

Из этой формулы следует, что с понижением температуры число частиц на высотах, отличных от нуля, убывает (рис. 8.10), обращаясь в 0 при Т=0 (при абсолютном нуле все молекулы расположились бы на поверхности Земли). При высоких температурах n слабо убывает с высотой, так

	что молекулы оказываются распределёнными по высоте почти равномерно. Распределение молекул по высоте является результатом конкуренции между притяжением молекул к Земле и тепловым движением, стремящимся разбросать молекулы по всем высотам. На разной высоте молекула обладает различным запасом потенциальной энергии
Рис. 8.10

.Следовательно, распределение молекул по высоте является и распределением их по значениям потенциальной энергии.

(*)

где 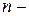плотность молекул в том месте пространства, где потенциальная энергия молекулы имеет значение ; плотность молекул в том месте, где потенциальная энергия равна 0.

Больцман доказал, что распределение (*) справедливо не только в случае потенциального поля сил земного тяготения, но и в любом потенциальном поле сил для совокупности любых одинаковых частиц, находящихся в состоянии хаотического теплового движения.

Таким образом, закон Больцмана (*) даёт распределение частиц, находящихся в состоянии хаотического теплового движения, по значениям потенциальной энергии. (рис. 8.11)

Рис. 8.11

4. Распределение Больцмана при дискретных уровнях энергии.

Полученное Больцманом распределение относится к случаям, когда молекулы находятся во внешнем поле и их потенциальная энергия может применяться непрерывно. Больцман обобщил полученный им закон на случай распределения, зависящего от внутренней энергии молекулы.

Известно, что величина внутренней энергии молекулы (или атома) Е может принимать лишь дискретный ряд дозволенных значений . В этом случае распределение Больцмана имеет вид:

,

где число частиц в состоянии с энергией ;

коэффициент пропорциональности, который удовлетворяет условию

,

где N – полное число частиц в рассматриваемой системе.

Тогда и в результате для случая дискретных значений энергии распределение Больцмана

	Качественная иллюстрация этого распределения представлена на рис. 8.12. Это распределение характерно для состояния термодинамического равновесия. Заметим, что в активных средах лазеров населённость уровней с большим значением энергии может быть выше, чем с меньшим. Это так называемая инверсная населённость уровней.
Рис. 8.12

Но состояние системы в этом случае термодинамически неравновесное.

5. Статистика Максвелла-Больцмана

Распределение Максвелла и Больцмана можно объединить в один закон Максвелла-Больцмана, согласно которому число молекул, компоненты скорости которых лежат в пределах от до 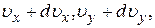, а координаты в пределах от x, y, z до x+dx, y+dy, z+dz, равно

где , плотность молекул в том месте пространства, где ; ; ; полная механическая энергия частицы.

Распределение Максвелла-Больцмана устанавливает распределение молекул газа по координатам и скоростям при наличии произвольного потенциального силового поля.

Примечание: распределение Максвелла и Больцмана являются составными частями единого распределения, называемого распределением Гиббса (этот вопрос подробно рассматривается в спецкурсах по статической физике, и мы ограничимся только упоминанием этого факта).

 

Вопросы для самоконтроля.

1. Дайте определение вероятности.

2. Каков смысл функции распределения?

3. Каков смысл условия нормировки?

4. Запишите формулу для определения среднего значения результатов измерения величины x с помощью функции распределения.

5. Что представляет собой распределение Максвелла?

6. Что такое функция распределения Максвелла? Каков ее физический смысл?

7. Постройте график функции распределения Максвелла и укажите характерные особенности этой функции.

8. Укажите на графике наиболее вероятную скорость . Получите выражение для . Как изменяется график при повышении температуры?

9. Получите барометрическую формулу. Что она определяет?

10. Получите зависимость концентрации молекул газа в поле силы тяжести от высоты.

11. Запишите закон распределения Больцмана а) для молекул идеального газа в поле силы тяжести; б) для частиц массой m, находящихся в роторе центрифуги, вращающейся с угловой скоростью .

12. Объясните физический смысл распределения Максвелла-Больцмана.

Лекция №9

Реальные газы

План

1. Силы межмолекулярного взаимодействия в газах. Уравнение Ван-дер-Ваальса. Изотермы реальных газов.

2. Метастабильные состояния. Критическое состояние.

3. Внутренняя энергия реального газа.

4. Эффект Джоуля – Томсона. Сжижение газов и получение низких температур.

1. Силы межмолекулярного взаимодействия в газах

Многие реальные газы подчиняются законам идеальных газов при нормальных условиях. Воздух можно считать идеальным до давлений ~ 10 атм. При повышении давления отклонения от идеальности (отклонение от состояния, описываемого уравнением Менделеева - Клайперона) возрастают и при p=1000 атм достигают более 100%.

Дело в том, что между молекулами действуют значительные по величине силы, называемые молекулярными силами. При удалении молекул друг от друга молекулярное взаимодействие проявляется в виде сил притяжения, при сближении – в виде сил отталкивания. Молекулярные силы имеют электромагнитное и квантовое происхождение. На рис. 9.1 а) представлена качественная зависимость сил межмолекулярного взаимодействия от расстояния r между молекулами, где Fотт и Fпр – соответственно силы отталкивания

Рис. 9.1

и притяжения, а F – их результирующая. Силы отталкивания считаются положительными, а силы взаимного притяжения – отрицательными. Соответствующая качественная кривая зависимости энергии взаимодействия молекул от расстояния r между центрами молекул приведена на

рис. 9.1б). На малых расстояниях молекулы отталкиваются, на больших притягиваются. Быстро возрастающие на малых расстояниях силы отталкивания означают грубо говоря, что молекулы как бы занимают некоторый определённый объём, дальше которого газ не может быть сжат.