Возникновение и развитие гравиметрии тесным образом связаны с развитием геодезии и геофизики, практические задачи которых оказывают все возрастающее влияние на гравиметрию и градиентометрию.
Выделяют четыре этапа развития гравиметрии:
Первый этап охватывает становление теоретических основ (17–18 вв.), что связано с общим подъемом науки и техники, вызванными великими географическими открытиями (15–16 вв.).
Галилео Галилей (1564–1642) экспериментировал с падающими телами и телами, движущимися по наклонным плоскостям, в результате им были открыты законы инерции и свободного падения тел. Им также была установлена зависимость периода колебания маятника от его длины. Эти пионерские исследования Г. Галилея послужили основой Христиану Гюйгенсу (1629–1695) для создания теории математических и физических маятников и к созданию первых маятниковых часов, а на их основе и первых маятниковых гравиметров.
Создание и совершенствование маятниковых гравиметров длилось около двух веков (18–19 вв.) и явилось вторым этапом развития гравиметрии.
Совершенствование маятниковых гравиметров опиралось на теорию маятника Гюйгенса, где была найдена зависимость периода колебаний маятника от широты пункта наблюдения.
Исаак Ньютон (1643–1727) создал теоретические основы механики, открыл законы динамики и закон всемирного притяжения
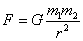 ,
,
что позволило определить фигуру равновесия жидкой однородной Земли, выявив при этом эффект полярного сжатия.
Эти работы получили дальнейшее развитие в исследованиях Леонарда Эйлера (1707–1783), внесшего основополагающий вклад в теорию вращения тел. П. Буге (1698–1758) вводит понятие уровенной поверхности и распространяет свои исследования на фигуры равновесия вращающихся тел, состоящих из концентрических слоев. А.К.Клеро (1713–1765) сформулировал гравиметрический метод, позволяющий определять гравитационные и геометрические параметры Земли по измерениям ускорений силы тяжести (теорема Клеро).
К этому же этапу относится становление и развитие потенциала в трудах Ж.Л. Лагранжа (1736–1813), П.С. Лапласа (1749–1827), А.М. Лежандра (1752–1833), С.Д. Пуассона (1741–1840), которыми было завершено создание математического аппарата гравиметрии и градиентометрии.
К концу этого этапа, благодаря обширным гравиметрическим съемкам, имелись в наличии огромные массивы данных гравиметрических измерений ускорений силы тяжести по всему земному шару.
Ф.Р. Гельмерт (1843–1917) вносит фундаментальный вклад в эту область. Им впервые было получено динамическое сжатие земного эллипсоида (1/298.3), предложено ввести понятие «нормального эллипсоида» и формулы для вычисления нормальной силы тяжести.
Третий этап в развитии гравиметрии (он одновременно является этапом возникновения и развития градиентометрии) характерен созданием (в 1930 г.) и быстрым совершенствованием статических гравиметров.
В этих приборах положение равновесия пробных масс в поле силы тяжести Земли компенсируется или упругой пружиной, или крутильной нитью. По изменениям положений пробной массы или угла ее поворота, выявленных из наблюдений с прибором на двух пунктах, можно получить величину изменения ускорения силы тяжести, если известен калибровочный коэффициент.
К настоящему времени точность статических гравиметров составляет ±10–8 м×с –2 ¸10–7 м×с –2.
Последним современным этапом в развитии гравиметрии следует считать создание морских гравиметров на стабилизированной платформе и баллистических гравиметров вышеуказанного уровня точности.
Возникновением градиентометрии следует полагать создание венгерским ученым Р. фон Этвешем (1848–1919) прибора, получившего название «крутильных весов» с пробными массами, расположенными на разной высоте, который позволял определять горизонтальные градиенты ускорения силы тяжести.
В середине ХХ в. важным стимулом к развитию градиентометрии послужили успехи инерциальной навигации, как наземной, так и морской и авиационной, где потребовались высокоточные акселерометры и гироскопы. Первые измеряют ускорение, а гироскоп удерживает с соизмеримой точностью стабилизацию измерительной платформы. Не последнюю роль в создании градиентометров сыграли и возможности современной вычислительной техники. Определенный вклад в становлении градиентометрии внесли успехи инерциальной гравиметрии.
Создание гравитационных градиентометров различных типов (поступательного или вращательного движений) с использованием нанотехнологий, т.е. 10–9 от единиц ускорения, позволяют измерять все компоненты тензора градиентов ускорения силы тяжести (тензора Этвеша) (1.5).
Измерение градиентов на поверхности Земли сопряжено со значительными трудностями, так как необходимо учитывать влияние масс ближних и дальних зон. Но при учете этих масс ошибки в их определении, вызванные неточностью в знании объема и плотности этих зон, как правило, на порядки превосходят ошибки в измерении самих градиентов. При измерениях на водной поверхности и на борту самолета (морская и самолетная градиентометрия) влияние ближних и дальних зон значительно ослабевают, но сильно возрастают ошибки в определении инерциальных ускорений, вызываемых изменениями скорости судов, их качкой и болтанкой, как на море, так и в воздухе.
Спутниковая градиентометрия в значительной степени освобождена от влияния ближних и дальних зон, но разрешающая способность в определении градиентов уменьшается обратно пропорционально кубу высоты градиентометра над поверхностью Земли.
В спутниковой градиентометрии различают два способа измерения градиентов:
- при помощи градиентометра, расположенного на борту спутника или расположенного за бортом орбитальной станции (на тросу),
- с помощью системы спутников («спутник–спутник» – два или более на одной орбите, то же, но на разных орбитах, оба случая с привлечением глобальных спутниковых систем («GPS», «ГЛОНАСС», затем «GALILEO») или геодезических систем типа «Doris» и т.п.).
Последний способ использует сам спутник в качестве пробной массы при определении градиентов гравитационного поля Земли.
Развитие спутниковой градиентометрии в настоящее время находится в начальной, экспериментальной стадии.
Первым экспериментальным проектом был «ARISTOTELES» (Европейское космическое агентство – ЕКА), но его реализация не была полностью успешной. Частью проекта «ARISTOTELES» был проект «GRADIO» (Франция). В этих проектах точность градиентометрических измерений составляла 10–2 ¸10–3 этвеша.
В проектируемой миссии SGG (Superconducting Gravity Gradiоmetr, США) разработчики применяют технологии сверхпроводимости, за счет чего ожидаемая точность должна составить 10–4 этвеша.
В последние годы ЕКА разработало и реализовало несколько проектов.
В марте 2002 года с космодрома «Плесецк» ЕКА вывело на орбиту 2 спутника по программе “GRACE” (Gravity Recovery And Cliмate Experiment), которые предназначены решать задачу градиентометрии в системе «спутник–спутник» (SST),без градиентометра на борту.
Второй проект “CHAMP” (CHAllenging Minisatellite Payload) разрабатывался в основном в Германии и по этому проекту в июне 2002 года с космодрома «Плесецк» одной ракетой было запущено несколько спутников, на одном из которых находился акселерометр. Этот проект использовал наблюдения SST и имел своей целью уточнение модели гравитационного поля EGM–96 до 360 гармоники включительно. Миссия этого проекта оказалась успешной.
Третий проект ЕКА получил название GOCE (Gravity field and Steady–state Ocean Circulation Explorer) и запланирован к реализации в 2007 году.
В этом проекте, помимо системы «спутник–спутник–GPS», на борту установят градиентометр. Планируют значительно уточнить EGM–96, причем, если сейчас ошибки этой модели дают величины порядка 50см., то после реализации этого проекта они должны уменьшится до 3см.
На подходе реализации находится и американский проект SGGM (Superсоnduction Gravity Gradiometr Mission) точность которого 2–3 Мгала с разрешением в 50 км., что эквивалентно 10–4 этвеша или гармоникам 500–го порядка и степени.
Из сказанного ясно, насколько актуальны и важны исследования по градиентометрии. Эти исследования необходимы для решения как фундаментальных, так и для прикладных задач.