Системы координат, используемые в градиентометрии

Рис 1.1

В градиентометрии наиболее часто встречающимися системами координат являются (рис.1.1):

1. Инерциальная (абсолютная, равноденственная, небесная, и другие названия) система координат, где основная плоскость xOy – плоскость небесного экватора, главная плоскость, xOz– плоскость колюра равноденствий.

2. Вращающаяся система координат, жестко связанная с Землей с угловой скоростью w_Å=0.721151467×10^–4 рад/сек. (это – гринвичская система координат для Земли), где основная плоскость ХОУ – земной экватор, главная плоскость XOZ – гринвичский меридиан. Данную систему координат представляют:

– Топоцентрические (инструментальные) системы координат с началом, расположенным на поверхности Земли в месте измерения (пункт Р):

а) горизонтная система (на рис.1.1 не показана), в которой основная плоскость x_h, p, y_h – плоскость горизонта, ось p, x_h направлена к полюсу, главная плоскость x_h, p, z_h – местный меридиан, ось p, z_h направлена в зенит.

б) локальная система, в которой основная плоскость x_L, p y_L – плоскость горизонта, ось p, x_L – направлена к полюсу, главная плоскость x_L, p z_L – расположена в плоскости меридиана, ось p z_L направлена в надир.

Ось p, y в обеих системах дополняют системы до правой.

Локальная система x_L, p y_L z_L зачастую является вращающейся вокруг оси p z_L, которая жестко скреплена с горизонтальной платформой вращающейся с угловой скоростью w_п и связанная с гринвичской системой углами Эйлера W, i, w.

– Спутникоцентрическая система координат с осями направленными вдоль подвижного триэдра S, T, W, стороны которого являются проекциям ускорения спутника на оси. При этом sS – радиальная составляющая направлена вдоль радиус–вектора , sT – трансверсальная составляющая лежит в плоскости орбиты и направлена в сторону движения ИСЗ, перпендикулярно , а sW – бинормальная составляющая ускорения спутника дополняет систему до правой перпендикулярно плоскости оскулирующей орбиты.

Инерциальная система координат. Исторически со времен Птолемея, когда считали Землю неподвижной, сложилось так, что инерциальная система привязана к экватору Земли, а, следовательно, и оси вращения Земли, а последняя за счет прецессии и нутации оси вращения Земли является слабовращающейся с периодами в 26 000 лет, 18 лет и так далее. Поэтому система становится инерциальной, если мы её отнесем к некоторому моменту времени t₀ (эпоху).

Если предположим, что нам задан единичный вектор на эпоху t₀,то удобнее систему редуцировать с эпохи t₀ (начало столетия 2000.0 0^h0^m)на момент наблюдений t:

(1.6)

Обратную связь получают в следующем виде

, (1.7)

где N –матрица нутации, П–матрица прецессии.

Так как N и П – ортогональные матрицы, то (N ×П)^–1=(N ×П)^Т.

Гринвичские системы. В гринвичских системах координатные оси жестко связаны, с вращающейся с угловой скоростью w _Å, и Землёй, поэтому радиус–вектор можно редуцировать в гринвичскую при помощи известных формул:

(1.8)

где S –матрица звездного времени т.е.

Единичный радиус–вектор отнесен к мгновенным плоскостям экватора и гринвичского меридианов. Их необходимо редуцировать на эпоху 1900–1905гг., то есть привести к среднему полюсу и экватору (МУН):

, (1.10)

где Р – матрица свободной нутации(или матрица движения земного полюса).

Явный вид всех вышеприведенных матриц имеются во всех учебниках по астрономии и геодезии.

Формулы связи для координат, скоростей и ускорений. В градиентометрии, небесной механике и космической геодезии полезно иметь формулы преобразования для полного вектора состояний: координат, скоростей и ускорений.

Предположим, на быстродвижущемся объекте М находятся приемники GPS или ГЛОНАСС и имеется возможность получать сразу координаты объекта М в общеземной геодезической системе (WGS–84 или ПЗ–90).

Полагая, что измерения проводятся в динамическом режиме, и при этом производится высокоточная регистрация времени t, тогда мы можем определять координаты, скорость и ускорение объекта М, т. е.

(1.11)

В этом случае необходимость использования вышеописанных алгоритмов отпадает, т.к. координаты объекта М получают непосредственно в общеземной системе координат, предварительно выполнив параллельный перенос.

Необходимо рассмотреть задачу перехода от общеземной (ITRF) к инерциальной системе координат (ICRS), где связь для объекта М имеет вид

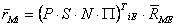, (1.12)

где Р – матрица перехода от мгновенных координат к средним (учет движения полюсов относительно земной поверхности), S – матрица, учитывающая вращение Земли (матрица звездного времени), N – матрица вынужденной нутации, П – матрица прецессии. Явный вид перечисленных матриц имеется в любом учебнике по космической геодезии, сферической астрономии или астрометрии. Введем обозначение

H_iE=(P×S×N ×M)^T_iE. (1.13)

Тогда для выражения (1.12) с учетом(1.13), выполнив дифференцирование, мы получим следующие формулы:

С учетом вышеизложенных обобщений, переход от общеземной к инерциальной системе можно представить в виде

(1.15)

где , имеет вид (1.11),а матрица X _iM является блочной матицей, каждый элемент которой в свою очередь представляет собой матрицы размером 3 на 3 и имеет следующий вид

Рассмотрим структуру матрицы H _iE. Все матрицы (за исключением S), входящие в неё согласно (1.13), весьма медленно меняются с течением времени. В самом деле, эти изменения не превышают:

– для матрицы Р – (1)" дуги в год,

– для матрицы N –(10)" дуги в год,

– для матрицы M –1'дуги в год.

В геодезической и астрономической практике эти изменения учитывают на промежутках времени значительно превышающие годичные и учитывают их, как мгновенные. Что касается матрицы S, то хотя она и осуществляет непрерывное вращение, но с целью унификации преобразования, её учитывают, как мгновенный поворот на величину звездного времени s. Это касается преобразования координат, т.е. первой строки блочной матрицы X _iE.

Что касается преобразования скоростей и ускорений, то мы вынуждены выполнять непрерывные вращения, т.к. в матрицах преобразования в явном виде входит угловая скорость вращения Земли. В самом деле, полагая зависящим от времени t только матрицу S, имеем

(1.17)

где матрица W есть матрица угловой скорости Земли .

В связи с тем, что ось вращения Земли и в инерциальной и в общеземной системах практически совпадает с осями оz и oZ, то матрица W имеет вид

или точнее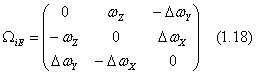

Аналогично для преобразования ускорений имеем

. (1.19)

С учетом (1.17) и (1.19) блочную матрицу X _iE в выражении (1.15) можно представить в виде

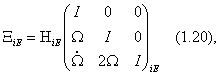
где I –единичные матрицы размером 3 на 3, а вид матриц приведены выше. Таким образом, преобразование (1.15),где матрица X _iE имеет вид(1.20) и формулы (1.15)–(1.20) решают задачу преобразования координат, скоростей и ускорений из общеземной системы координат в инерциальную.

Для получения формул обратного перехода достаточно транспонировать отдельно каждую из матриц, составляющих блок матрицы X _iE, т.е.

, (1.21)

где M_Ei – транспонированная по блокам матрица X _iE.

Связь между вращающейся спутникоцентрической и инерциальной системами координат. Пусть нам задана инерциальная система координат xoyz и спутникоцентрическая система (рис.1.1), где sS – проекция возмущающего ускорения на продолжения радиус–вектора , т.е. радиальная составляющая возмущающего ускорения S, sT – проекция возмущающего ускорения на перпендикуляр к радиусу–вектору, направленный в сторону движения спутника, т.е. трансверсальная составляющая T, sW – проекция возмущающего ускорения на перпендикуляр к радиальной и трансверсальной составляющим, дополняющий систему до правой, т.е. бинормальная составляющая W.

Связь координат спутника, определяющих радиус–вектор будет иметь вид

где первый столбец направляющих косинусов имеет вид

а второй и третий столбцы находят простым дифференцированием по u и i:

Формулы (1.22)–(1.25) полностью решают задачу связи инерциальной и спутникоцентрической систем координат. В этих формулах u = w+n, W, i – являются элементами орбиты спутника.

 

 

Введение в теорию поля

Скалярное поле. Скалярная величина U, которая принимает определенные значения в каждой точке М заданного пространства D, называется скалярной функцией точки или скалярным полем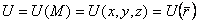

Примеры скалярных полей:

- поле температур

- поле плотностей

- поле давлений

- поле потенциала притяжения

- электромагнитное поле

- поле напряженности в электростатическом поле и так далее.

Поле в зависимости от размерности задания точки может быть: одномерным M(x), двухмерным M(x, y), трехмерным M(x, y, z) и т. д., например, n-мерным M(x¹,x²,…xⁿ).

Центральное поле. Если функция принимает равные значения для всех точек, находящихся на равном расстоянии от центра О, то поле называют центральным или сферическим полем.

В этом случае функция U зависит только от расстояния до центра О, то есть .

Примеры центральных полей:

- – уравнение сферической поверхности с радиусом и центром в точке О.

- – квадрат расстояния от центра О,

- – потенциал точки О с массой равной 1.

- – потенциал любой планеты, представленной точечной массой m_n, где f – постоянная Ньютона.

- – выражает освещенность в зависимости от расстояния до центра О, т.е. на расстоянии освещенность будет равна .

Координатное задание скалярного поля. Введем декартовую, сферическую или какую-либо другую систему координат, совместив её начало с центром О. В этом случае скалярное поле можно задать в координатном виде:

декартовая система

сферическая – и так далее.

Выражение для задания центрального поля:

Поверхности одинакового уровня. Точки, для которых функция принимает одинаковые значения, образуют в пространстве поверхности одинакового уровня, то есть U = const.

Примеры:

- – это класс параллельных плоскостей.

-

-

Это выражение представляет собой вложенные друг в друга сферы с радиусом . То же и , но в этом случае радиус определяется, как , то есть c²=x²+y²+z².

- В точке О точечный излучатель тепла, тогда изотермы (сферы) будут поверхности одинаковой температуры.

- Для сферического распределения давления изобары – поверхности (сферы) одинакового давления.

- Для сферической Земли на ее физической поверхности сферы с одинаковыми высотами будут задавать нам горизонтали.

Векторное поле. Векторная величина , которая принимает определенное значение в каждой точке М пространства, называется векторным полем .

Обобщающим примером векторных полей могут служить поля изменений скалярных величин: изменения температур, изменения плотности, изменения потенциала силы тяжести и т.д. Векторное поле может быть: двухмерное, трехмерное и т.д.

Типы векторных полей:

– Центральное векторное поле. В этом поле все вектора лежат на прямых, пересекающихся в одной точке О (центре). Если поместить полюс в начало, т.е. в точку О, то в этом случае и эту векторную функцию можно представить в виде: .

– Сферическое векторное поле. Это важный частный случай центрального поля, на которое наложено дополнительное ограничение, а именно, длина вектора зависит от расстояния к точке О, т.е. .

Пример: Притяжение тел на основе закона всемирного притяжения прямо пропорционально квадрату расстояния между ними

Координатное задание векторного поля. Векторное поле всегда можно определить с помощью скалярных полей. Так в трехмерном пространстве векторное поле однозначно определяется тремя скалярными полями , являющихся коэффициентами разложений по трем некомпланарным векторам .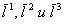

Имеем . Связь декартовых и сферических координат составляют известные формулы:

Связь между скалярными величинами, характеризующими один и тот же вектор в декартовой и сферической системах координат, имеет вид:

Отметим немаловажную деталь: матрицей преобразования проекций векторов служит матрица частных производных (якобиан). Такие матрицы в линейных n-мерных системах координат являются обобщением объектов, получивших название тензоров.

Безвихревое поле. Пусть мы имеем скалярную функцию векторного аргумента . Заметим, что значение функции есть число (скалярное) в любой координатной системе . Кроме того, пусть мы имеем векторную функцию от векторного аргумента .

Градиентом скалярной функции векторного аргумента называют векторную функцию, определяемую формулой , а оператор набла (Ñ) даётся формулой .

Дивергенцией (divergensia – разложение) векторной функции называют скалярную функцию, определяемую формулой .

Ротор векторной функции это векторная функция векторного аргумента, определяемая формулой .

Безвихревыми называют такие поля, у которых ротор равен 0.

Рассмотрим произвольную систему координат (с осями 0x₁, 0x₂, 0x₃ и ортами ).

а) Градиент от абсолютного скалярного (для трехмерного) пространства есть вектор.

б) Градиент от абсолютного вектора представляет собой тензор 2-ого ранга (диадик).

, (1.30)

где ,а – градиент (локальный аффинор) вектора .

в) Дивергенция дает скалярную характеристику векторного поля (плотность, интенсивность, значение потенциала и т.д.) .

В тензорной записи – это скаляр и в нашем случае j=1, 2, 3, то есть абсолютный скаляр, который характеризуется числом .

В декартовой трехмерной системе координат градиент от скалярной функции будет иметь вид

Тождественная запись в векторной форме

Выражение (1.32) представляет собой матрицу-столбец вектора с компонентами

В векторном анализе градиент от векторной функции отсутствует. Если руководствоваться тензорным исчислением, то градиент от градиента или градиент от векторной функции будет иметь вид

где матрица в (1.33) является локальным аффинором вектора Дивергенция от вектора в декартовой системе координат имеет вид

Выражение (1.34) есть скаляр, равный сумме производных от проекций вектора Еще раз напомним, что в безвихревом поле ротор

(1.35)

г) При повторном применении оператора Ñ (оператора Гамильтона) в безвихревом поле имеют место 3 операции:

В первом случае берется дивергенция от градиента

Выражение Ѳ· V получило название оператора Лапласа, а выражение (1.38) получило название Лапласиана.

Во второй операции выражений (1.36) градиент от дивергенции, есть вектор, компонентами которого являются суммы вторых производных.

В тензорном исчислении последняя третья операция правомерна, т.к. имеет место градиент от абсолютного вектора и от тензора. Что касается векторного исчисления, то градиент там вводится только от скалярной функции. Но мы ввели в векторном исчислении градиент от векторной функции в виде (1.33).

Аналогично можно ввести и операцию «градиент от градиента»:

д) Операции над простейшими функциями от в безвихревом поле.

Функция j		rn	Ln r
Ñj
Ñ·j

\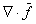