Предмет градиентометрии и решаемые задачи

Гравиметрия (gravis – тяжелый, тяжесть, metrew – измеряю) – наука об измерении ускорения сил тяжести Земли , при этом гравиметрия фактически измеряет только модуль ускорения силы тяжести:

, (1.1)

где W=U+C, а в свою очередь: W – потенциал силы тяжести Земли, U – потенциал сил притяжения Земли, С – потенциал центробежных сил.

Градиентометрия (gradio – шагаю, metrew – измеряю) – раздел гравиметрии, изучающий вторые производные потенциала W или первые производные от вектора силы тяжести , то есть

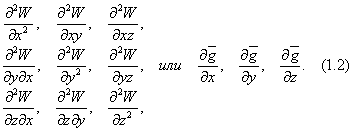
Отметим некоторые особенности терминологии, установившейся в гравиметрии и градиентометрии.

Согласно второму закону Ньютона, сила связана с ускорением следующим образом:

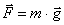, (1.3)

где m – масса, – вектор ускорения тела m.

Выражение (1.3) можно записать в следующем виде

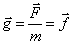, (1.4)

где 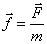– принято называть удельной силой. В этой связи и укоренился термин «ускорение силы тяжести», так как ускорение тела m тождественно равно удельной силе или пропорционально силе тяжести Земли.

Что касается термина «градиентометрия» (за рубежом принято «градиометрия»), то в русской транскрипции он произошел уже от сложившегося математического термина «градиент», который в векторном анализе применим только к скалярным функциям векторного аргумента (в нашем случае это 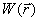или ) и нам он будет давать ускорения силы тяжести, которые изучают в гравиметрии.

В градиентометрии изучают градиент от векторной функции векторного аргумента, т.е. , что возможно только тензорном анализе.

В нашем случае это будет градиент от вектора ускорения силы тяжести или градиент от градиента потенциала силы тяжести, то есть

где а Ñ (набла) – дифференциальный оператор, действия с которым будут рассмотрены ниже.

Первая матрица, входящая в (1.5), представляет собой ковариантную производную вектора , и получила название градиента или локального аффинора этого вектора. Что касается матрицы вторых производных, то она получила название тензора Этвеша или полного тензора градиентов силы тяжести.

В международной системе СИ размерность ускорения силы тяжести – м/c² или мс^–2 , размерность составляющих градиента - 1/с² или с^–2.Применяются и более мелкие единицы 1 м/c² =10⁶мкм/ c² =10⁹нм/с². Но в геодезии и геофизике получили распространение несколько иные единицы, а именно стотысячная и одна стомиллионная стандартной единицы 1м/с², т.е. 1м/с²=10⁵ мГал =10⁸ микроГал.

Гал – это сокращение от имени великого итальянского ученого Галилео Галилея (1Гал = 1см/с²), который одним из первых установил, что свободные падения – это равноускоренное движение.

Для градиентов часто используют единицу Этвеш, то есть 1Е=10^–9с^–2=10^–1 мГал/км.

Эта единица введена в честь венгерского ученого Р. фон Этвеша (1848–1919гг), который первым определил горизонтальный градиент при помощи крутильных весов с разновысокими массами.

Отметим, что ускорение силы тяжести вызывается целым рядом сил потенциальной природы, но разного происхождения:

1. силой притяжения, вызываемой потенциалом Земли U.

2. центробежной силой, вызываемой вращением Земли.

3. силой притяжения Луны, Солнца и др. небесными телами.

4. силами, вызываемыми деформацией Земли из–за лунно–солнечных приливов и т.д.

То есть

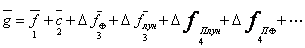(1.6)

Все перечисленные составляющие ускорения силы тяжести (1.6) входят и в градиенты от ускорения силы тяжести (1.5).

Задачей гравиметрии и градиентометрии является определение гравитационного поля Земли и других небесных тел (планетарная гравиметрия) как функции местоположения и времени по измерению ускорений силы тяжести и гравитационных градиентов на поверхности или вблизи тела.

Еще раз подчеркнем, что определение полного вектора силы тяжести 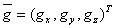не относят к задачам гравиметрии. Гравиметрия определяет только модуль , а иногда и , а направляющие косинусы вектора определяют геодезическая астрономия и высшая геодезия, получая уклонение силы тяжести и аномалии высот, как разность астрономических и геодезических координат.