Задачи транспортного типа
Классическая транспортная задача
Имеется р пунктов производства (поставщики) и q пунктов потребления (потребители) некоторого однородного продукта.
 - объемы производства в пунктах производства k (k=1,…,p);
- объемы производства в пунктах производства k (k=1,…,p);
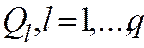 - объемы потребления в пунктах потребления l;
- объемы потребления в пунктах потребления l;
 - затраты, связанные с перевозкой единицы продукта из пункта р производства в пункт q потребления.
- затраты, связанные с перевозкой единицы продукта из пункта р производства в пункт q потребления.
Требуется прикрепить пункты производства к пунктам потребления таким образом, чтобы суммарные расходы на транспортировку были минимальными.
Задача инвестиционного управления
Дано: m инвесторов, владеющих инвестициями в количествах  .
.
Инвесторы могут использовать свои инвестиции в n инвестиционных проектах с потребностями инвестиций в объемах  .
.
Известны нормативные коэффициенты эффективности  использования единицы инвестиций i -го инвестора в j -ом проекте.
использования единицы инвестиций i -го инвестора в j -ом проекте.
Требуется определить инвестиционные потоки  , направляемые от i -го инвестора к j -ому инвестиционному проекту таким образом, чтобы получить максимальную эффективность от инвестирования.
, направляемые от i -го инвестора к j -ому инвестиционному проекту таким образом, чтобы получить максимальную эффективность от инвестирования.
Математическая модель
Пусть  , i=1,…,m; j=1,…,n
, i=1,…,m; j=1,…,n
Найти инвестиционные потоки  , направляемые от
, направляемые от  − го инвестора
− го инвестора  − у инвестиционному проекту, удовлетворяющие условиям:
− у инвестиционному проекту, удовлетворяющие условиям:
1. 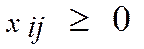 , i=1,…,m; j=1,…,n
, i=1,…,m; j=1,…,n
2. 

3. 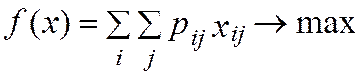
Возможны случаи:
а)  − общее количество инвестиций равно суммарному объему требуемых для инвестиций средств
− общее количество инвестиций равно суммарному объему требуемых для инвестиций средств  модель называется закрытой;
модель называется закрытой;

 б)
б) 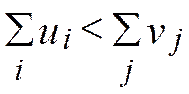
 модель открытая
модель открытая  модель закрытая
модель закрытая  вводится фиктивный инвестор
вводится фиктивный инвестор 
в) 
 модель открытая
модель открытая  модель закрытая
модель закрытая  вводится фиктивный проект с объемом средств
вводится фиктивный проект с объемом средств 
 нормативные коэффициенты эффективности
нормативные коэффициенты эффективности  полагают равными нулю.
полагают равными нулю.
Теорема 1. Среди  ограничений ЗИУ одна строка (любая) линейно зависима от других.
ограничений ЗИУ одна строка (любая) линейно зависима от других.
Доказательство. Из теоремы следует, что из системы ограничений одну строку (любую) можно исключить.
О наличии линейно- зависимых строк можно убедиться, суммируя m строк и n строк ограничений 2:
 (1)
(1)
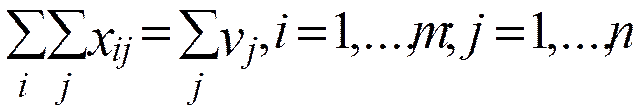 (2)
(2)
Так как 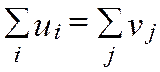 , получили два одинаковых уравнения (1), (2). Наличие в системе ограничений двух одинаковых уравнений говорит об ее линейной зависимости.
, получили два одинаковых уравнения (1), (2). Наличие в системе ограничений двух одинаковых уравнений говорит об ее линейной зависимости.
Если одно из уравнений системы ограничений отбросить, то система линейных уравнений будет содержать (m+n -1) линейно-независимых уравнений.
Следовательно, ЗИУ будет иметь размерность (m+n -1)х(m+n -1)▄
Теорема 2. В оптимальном решении ЗИУ не может быть более (m+n -1) ненулевых компонентов  , если оптимальное решение единственное.
, если оптимальное решение единственное.
Пример.
Дано: m =3, n =4, 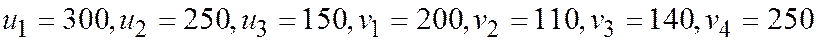
 , т.е. имеем закрытую модель
, т.е. имеем закрытую модель
Схема инвестиционных потоков
 =200
=200  =110
=110  =140
=140  =250
=250
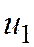 =300 =300
|  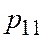 =3 =3
|  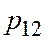 = 5 = 5
| 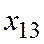 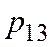 =4 =4
|   =6 =6
|
 =250 =250
|   = 2 = 2
| 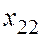  = 4 = 4
|   = 3 = 3
|   =1 =1
|
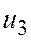 =150 =150
| 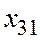  =5 =5
| 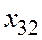  =3 =3
| 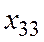  =4 =4
|   =9 =9
|
Размерность задачи:  .
.
Матрица нормативных коэффициентов эффективности:

Требуется найти
 при ограничениях:
при ограничениях:
1.  ≥0, i= 1,2,3; j =1,2,3,4
≥0, i= 1,2,3; j =1,2,3,4
2. 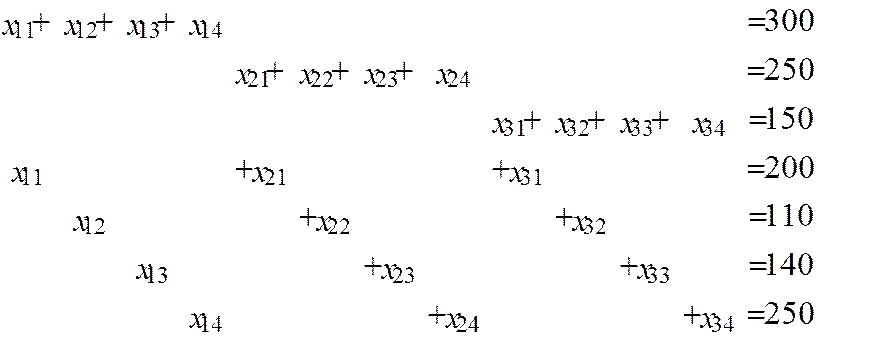
Метод потенциалов
1. Нахождение исходного допустимого базисного решения с помощью метода северо-западного угла, вычисляется значение целевой функции.
2. Вычисление оценок  свободных клеток,
свободных клеток,
при этом, если оптимальное решение не получено, то нужно перейти к другому базисному решению.
3. Вычисление для полученного решения целевой
функции (значение целевой функции должно улучшаться).
4. Шаги 2, 3 продолжаются до тех пор, пока не
получится оптимальное решение, т.е. все оценки свободных клеток  должны быть неположительными, т.е.
должны быть неположительными, т.е.  . При этом f (х)будет принимать максимальное значение. Если все
. При этом f (х)будет принимать максимальное значение. Если все  , то решение единственное, если есть
, то решение единственное, если есть  = 0, то решение может быть неединственным, так как на текущей итерации имеется возможность перехода к другому базису, не меняя значение целевой функции.
= 0, то решение может быть неединственным, так как на текущей итерации имеется возможность перехода к другому базису, не меняя значение целевой функции.
Пример (метод северо-западного угла)
Исходные данные Метод северо-западного угла
| (1,1):  , ,  (1,2):
(1,2): 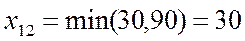 , ,  (2,2):
(2,2):  , , 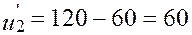 (2,3):
(2,3):  , ,  (3,3):
(3,3): 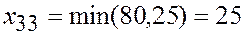 , ,  (3,4):
(3,4): 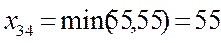
|
1. Нахождение исходного допустимого базисного решения с помощью метода северо-западного угла (полностью используются инвестиционные возможности инвесторов и полностью удовлетворяются потребности проектов в инвестициях):
Исходные данные Метод северо-западного угла

|
|
Число базисных решений (занятых клеток) 
Исходное допустимое решение:
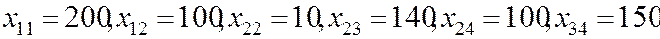 , остальные – 0, f (x)=3010
, остальные – 0, f (x)=3010
Занятая клетка → базисным переменным. Свободная клетка → небазисным переменным
2. Вычисление оценок  свободных клеток (Итерация 1)
свободных клеток (Итерация 1)
| · в незанятую клетку (1,3) ставим «+»  незанятая клетка стала занятой (базисной) незанятая клетка стала занятой (базисной)  количество занятых клеток количество занятых клеток   появляется цикл, все вершины которого, кроме клетки (1,3), находятся в занятых клетках.
· Отыскиваем цикл появляется цикл, все вершины которого, кроме клетки (1,3), находятся в занятых клетках.
· Отыскиваем цикл
| |||||||||||||||||||||
| Правило построения цикла: · Начиная с клетки «+» поочередно проставляем знаки «+» и «–». · Направление движения в цикле - по часовой стрелке или против нее. · Вершины цикла находятся в занятых клетках. · Стороны цикла могут проходить мимо некоторых занятых клеток и могут пересекаться.. · для каждой небазисной переменной существует только единственный цикл по теоремам 4, 6 |
| |||||||||||||||||||||
При вычислении оценки  свободной клетки нормативные коэффициенты свободной клетки нормативные коэффициенты  , соответствующие клеткам «+», берутся со знаком «+», а клеткам «−» берутся со знаком «−»: , соответствующие клеткам «+», берутся со знаком «+», а клеткам «−» берутся со знаком «−»: 
|
| |||||||||||||||||||||
| 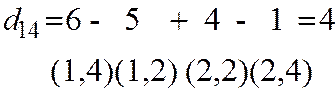

|
| 
|
|

|
|

|
|

|
Среди вычисленных оценок есть положительная:  , т.е. исходное решение не оптимальное:
, т.е. исходное решение не оптимальное:

Переход к новому допустимому решению
Пусть 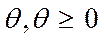 – количество инвестиций, которое следует перераспределить по данному циклу.
– количество инвестиций, которое следует перераспределить по данному циклу.
Цикл перераспределения инвестиций от 1-го инвестора на выполнение 4-го проекта
100– θ
  (1,2) (1,2)
|  + θ
(1,4) + θ
(1,4)
|
(2,2)
 10+ θ 10+ θ
| (2,4) 100– θ |
· Находим θ =min  , где
, где  − инвестиции, стоящие в вершинах цикла, отмеченных знаком «– ».
− инвестиции, стоящие в вершинах цикла, отмеченных знаком «– ».
· Если  соответствуют несколько минимальных инвестиций, то при вычитании оставляем в соответствующих клетках нулевые инвестиции в таком количестве, чтобы во вновь полученном решении занятых клеток было m+n - 1.
соответствуют несколько минимальных инвестиций, то при вычитании оставляем в соответствующих клетках нулевые инвестиции в таком количестве, чтобы во вновь полученном решении занятых клеток было m+n - 1.
θ =min(100,100)=100. 
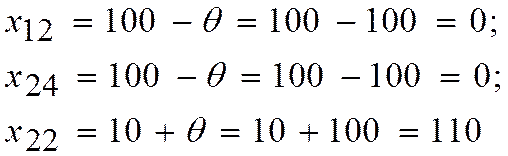
Следует выбрать одну из переменных
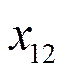 или
или  .
.
Так как  , оставляем
, оставляем 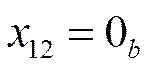 .
.
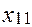
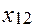


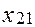







 =
=70
=
=70
 =
=90
=
=90
 =
=85
=
=85
 =
=55
=
=55

 _
_
 –
+
–
+
 +
+

 -
-
 +
+
 +
+

 _
_
 +
+
 +
+

 200
_
200
_ 
 100
+
100
+
 10
_
10
_
 100
+
100
+
 +
+

 10
-
10
-
 100
+
100
+
 +
+

 -
-
 +
+
 +
+ 