Выпуклость графика функции, точки перегиба

ТЕМА «ПРИЛОЖЕНИЯ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ»

Правило Лопиталя

Теорема 1. (Правило Лопиталя раскрытия неопределённости вида )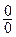

Если функции f (x)и g (x)дифференцируемы в окрестности точки , непрерывны в точке , отлична от нуля в окрестности точки и , то предел отношения функций при равен пределу отношения их производных, если этот предел существует:

 

 

Теорему принимаем без доказательств.

 

Теорема 2. (Правило Лопиталя раскрытия неопределённости вида )

Если функции f (x)и g (x)дифференцируемы в окрестности точки , непрерывны в точке , отлична от нуля в окрестности точки и , то предел отношения функций при равен пределу отношения их производных, если этот предел существует:

 

 

Теорему принимаем без доказательств.

 

Пример 1. Используя правило Лопиталя найти предел функции .

Решение. .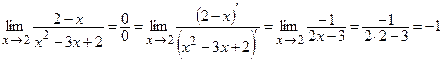

Пример 2. Используя правило Лопиталя найти предел функции .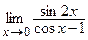

Решение. (самостоятельно)

 

Замечание: Правило Лопиталя применяют до тех пор, пока не избавятся от неопределённости.

Пример 3. Используя правило Лопиталя найти предел функции .

Решение.

Пример 4. Используя правило Лопиталя найти предел функции .

Решение. (самостоятельно)

 

 

Возрастание и убывание функции.

Определение. Функция 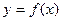называется возрастающей на , если

большему значению аргумента из этого интервала соответствует большее значение функции

Определение. Функция 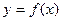называется убывающей на , если большему значению аргумента из этого интервала соответствует меньшее значение функции

Убывающая и возрастающая функции называются монотонными функциями.

 

Теорема 6. (Необходимые условия возрастания (убывания) функции) Если дифференцируемая функция 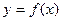возрастает (убывает) на , то ее производная неотрицательна (неположительна) на этом интервале: (или ).

Доказательство. Используем для доказательства теоремы геометрический смысл производной. Проведём в произвольных точках несколько касательных к графику возрастающей функции.

________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________

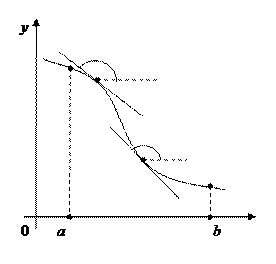
Рассмотрим, теперь, убывающую на функцию. Проведём к её графику несколько касательных в произвольных точках.

________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________

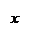Теорема 7. (Достаточные условия возрастания (убывания) функции) Если функция 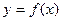непрерывна на промежутке и дифференцируема на интервале , причем 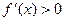(или ) для , то эта функция возрастает (убывает) на этом промежутке.

 

Теорему принимаем без доказательств.

 

 

Экстремум функции

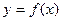Определение. Точка называется точкой максимума функции , если для всех точек из некоторой окрестности точки справедливо неравенство .

 

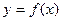Определение. Точка называется точкой минимума функции , если для всех точек из некоторой окрестности точки справедливо неравенство .

 

Значение функции в точке минимума (максимума) называется минимумом (максимумом) функции. Максимум (минимум) функции называется экстремумом функции.

 

Примем без доказательства следующую теорему.

Теорема 8. (Необходимое условие экстремума функции) Если функция 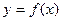, определённая в окрестности точки , достигает экстремума в самой точке , то ее производная в этой точке равна нулю (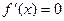) или не существует.

Геометрически равенство 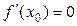означает _____________________________________________

____________________________________________________________________________________________________________________________________________________________________________________

 

 

Необходимое условие экстремума не является достаточным условием. То есть, если в точке производная функции равна нулю, то это не означает, что в точке существует экстремум функции.

Поясним это на примере функции 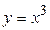. Производная данной функции в точке 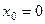равна нулю: однако в этой точке функция не имеет экстремума.

 

Существуют функции, которые в точках экстремума не имеют производной.

Например, непрерывная функция .

Почему в точке х = 0 функция не имеет производную? _____________________________________________________

____________________________________________________________________________________________________________________________________________________________________________________________________________________

 

Таким образом, непрерывная функция может иметь экстремум в тех точках, где производная равна нулю или не существует.

Определение. Точки, в которых производная функции равна нулю, называют стационарными точками. Точки, в которых первая производная функции равна нулю или не существует, называют критическими точками первого рода.

 

Примем без доказательства следующую теорему.

Теорема 9. (Достаточные условия экстремума функции) Пусть функция 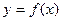дифференцируема в некоторой окрестности точки . Если в самой точке производная функции равна нулю и меняет знак при переходе через точку , то точка является точкой экстремума, причём:

1) если знак меняется с плюса на минус, то ─ точка максимума;

2) если знак меняется с минуса на плюс, то ─ точка минимума.

 

Пример. Найти интервалы возрастания и убывания и исследовать на экстремум функцию .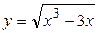

Решение. Находим область определения функции:

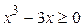или . Решив это неравенство методом интервалов, получаем .

Находим критические точки функции, то есть точки, в которых производная равна нулю или не существует.

.

Производная равна нулю, если числитель равен нулю, отсюда:

, то есть и 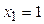, . При этом точка не входит в область определения функции и из дальнейшего анализа исключается.

Производная не существует, если знаменатель равен нулю, отсюда:

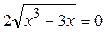, то есть или . Получаем: , , .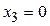

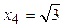Отмечаем найденные критические точки на числовой прямой (с учётом области определения заданной функции). Над числовой прямой в выделенных интервалах оцениваем знак производной, под числовой прямой анализируем поведение функции на этих интервалах.

 

Следовательно, функция в точке 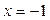имеет экстремум, а именно – максимум:

.

На интервалах и функция возрастает, на интервале - убывает.

 

Выпуклость графика функции, точки перегиба

 

Определение. Графикфункции называется выпуклым на , если он расположен ниже любой касательной, проведенной к графику на этом интервале.

Определение. Графикфункции называется вогнутым на , если он расположен выше любой касательной, проведенной к графику на этом интервале.

Интервалы выпуклости и вогнутости находят с помощью следующей теоремы.

Теорема 10. Пусть функция дифференцируема на интервале . Если во всех точках интервала вторая производная функции отрицательная, т.е. f ''(x) < 0, то график функции на этом интервале выпуклый, если же f ''(x) > 0 – вогнутый.

 

Принимаем эту теорему без доказательств, но поясним графически.

Рассмотрим случай выпуклой функции.

 

 

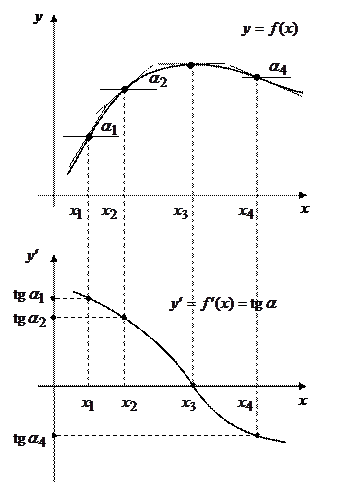
Проведём в нескольких точках касательные к графику функции и измерим углы наклона этих касательных к оси Ох. Угол в нашем случае равен нулю.

 

 

В плоскости 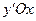на оси ординат будем откладывать значения тангенсов измеренных улов. Через точки 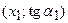, , 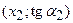, проведём кривую. Получим график первой производной .

 

Как видно из рисунка, первая производная выпуклой функции является убывающей функцией. А, как известно, производная убывающей функции в любой точке меньше нуля. То есть, , что и утверждается в теореме.

 

Определение. Точка графика непрерывной функции, отделяющая его выпуклую часть от вогнутой, называется точкой перегиба.

Замечание. В точке перегиба касательная, если она существует, пересекает кривую: с одной стороны от этой точки кривая лежит под касательной, а с другой стороны – над нею.

 

Примем без доказательства следующие теоремы.

Теорема 11 (необходимое условие перегиба). Для того чтобы точка являлась точкой перегиба дважды дифференцируемой функции , необходимо, чтобы ее вторая производная в этой точке равнялась нулю (f ''(x) = 0) или не существовала.

Теорема 12 (достаточное условие перегиба). Если вторая производная f ''(x) дважды дифференцируемой функции при переходе через некоторую точку меняет знак, то есть точка перегиба (при этом в самой точке вторая производная f ''(x) может и не существовать).

Определение. Критическими точками второго рода называются точки, в которых вторая производная дифференцируемой функции равна нулю или не существует

 

Пример. Исследовать на выпуклость, вогнутость и точки перегиба функцию .

Решение. Область определения функции - вся числовая прямая.

Для того чтобы найти интервалы выпуклости и вогнутости, находим критические точки второго рода.

; .

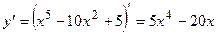Вторая производная существует на всей числовой оси. Будем искать точки, в которых она равна нулю.

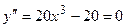
или .

Отмечаем найденную критическую точку на числовой прямой (с учётом области определения заданной функции). Над числовой прямой в выделенных интервалах оцениваем знак второй производной, под числовой прямой анализируем поведение функции на этих интервалах.

 

 

Следовательно, функция в точке имеет перегиб и .

На интервале функция выпукла, на интервале функция вогнута.