Напомним, что асимптотой кривой называется прямая, расстояние d до которой от точки М, лежащей на кривой, стремиться к нулю при неограниченном удалении от начала координат этой точки по кривой.
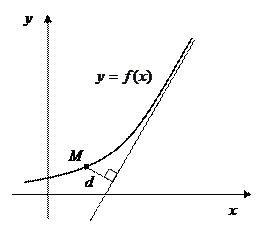
Уравнение вертикальной асимптоты 
;
уравнение горизонтальной асимптоты 
;
уравнение наклонной асимптоты 
,
где 
, 
.
Исследование функции 
можно проводить по следующей схеме:
1) находим область определения функции;
2) проверяем выполнение условий чётности и нечётности;
3) находим точки разрыва функции и определяем характер разрыва;
4) находим асимптоты графика функции;
5) находим критические точки первого рода, определяем интервалы возрастания и убывания графика функции, координаты точек экстремума;
6) находим критические точки второго рода, определяем интервалы выпуклости и вогнутости графика функции, координаты точек перегиба;
7) в соответствии с проведённым исследованием строим график функции (предварительно можно найти точки пресечения графика функции с осями координат).
Пример. Провести полное исследование функции 
и построить её график.
Решение. 1) Функция определена везде, кроме точки 
, т.е. 
.
2) Проверим выполнение условий чётности 
и нечётности 
:
,
следовательно, функция не является ни чётной, ни нечётной. Т.е. мы имеем дело с функцией общего вида.
3) Так как функция неопределенна только в точке х = –1, то именно здесь она и терпит разрыв. Исследуем характер этого разрыва.
, 
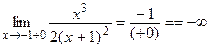
В точке 
у функции разрыв II рода (бесконечный разрыв), а прямая 
является вертикальной асимптотой графика функции.
4) Найдем наклонную асимптоту, задаваемую уравнением прямой 
. При вычислении пределов, определяющих коэффициент k и постоянную b, легко увидеть, что результат не зависит от знака бесконечности:
Следовательно, 
– наклонная асимптота.
Горизонтальной асимптоты 
нет, так как:
.
5) Для нахождения критических точек вычисляем первую производную заданной функции и приравниваем её к нулю, в соответствии с необходимым условием экстремума.
.
Отсюда, 
.
Производная равна нулю, если числитель полученной дроби равен нулю:
.
Производная не существует, если знаменатель полученной дроби равен нулю:
.
Получили три критические точки, которые, для удобства дальнейшего анализа, изобразим на числовой прямой. Оценим знак производной и поведение функции на полученных интервалах:
Видно, что при х = – 3 функция имеет максимум, минимумов у неё нет, так как при х = – 1 функция терпит разрыв, а в критической точке х = – 3 нет ни минимумов, ни максимумов, потому что при переходе через неё производная не сменила свой знак.
Найдем 
.
Итак, точка 
– точка максимума графика функции.
6) Для исследования функции на выпуклость, вогнутость и перегиб с используем вторую производную.
.
Ищем критические точки второго рода там, где вторая производная равна нулю или не существует. Для нашей производной получаем:
– критическая точка, в которой производная равна нулю, а из 
– критическая точка, в которой производная не существует. Отмечаем критические точки на числовой прямой:
На интервалах 
, следовательно, функция здесь выпуклая; на интервале 
, следовательно, функция здесь вогнутая. В точке х = 0 выпуклость сменяется вогнутостью, эта точка является точкой перегиба.
7) Перед построением графика функции найдём для него точки пересечения с осями координат:
- с осью абсцисс: 
, следовательно, получаем точку пересечения (0; 0);
- с осью ординат: 
, получаем ту же самую точку (0; 0).
Отмечаем на координатной плоскости точки экстремума, перегиба, пересечения с осями координат. Проводим асимптоты. Строим график (показано на рисунке ниже).
