Системы линейных уравнений

Задача 72. Решить систему линейных уравнений .

Решение. А. Матричным методом.

Запишем систему в виде: .

Найдём обратную матрицу для А.

= = = .

Б. Методом Крамера.

= = .

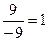Ответ. .

Задача 73. Решить систему уравнений

Решение. Построим расширенную матрицу и преобразуем её.

чтобы обнулились коэффициенты ниже левого верхнего угла, то есть чтобы исчезла переменная из всех уравнений кроме первого, надо:

а) из 2-й строки вычесть 1-ю;

б) из 3-й строки вычесть удвоенную 1-ю.

Теперь, чтобы обнулить ниже чем , нужно к 3-й строке просто прибавить 2-ю, так как знаки там противоположны. При этом структуру из нулей, которые уже получились слева, мы на последующем шаге всё равно никак не испортим, ведь там к 0 будет прибавляться 0 либо вычитаться 0, то есть ступенчатая структура там уже всё равно будет сохраняться.

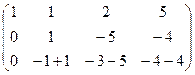Когда в основной матрице уже получена треугольная структура, снова перепишем в виде системы

В первом уравнении 3 неизвестных, а в каждом следующем всё меньше и меньше, а в последнем вообще только одна неизвестная. Именно этой цели мы и хотели добиться, приводя к треугольному виду: из последнего уравнения можно теперь сразу выразить . Затем с этой информацией мы поднимаемся в предпоследнее уравнение, где две неизвестных, впрочем, одна из них уже известна.

А теперь уже две последних неизвестных стали известны, и с этой информацией поднимаемся в 1-е уравнение, подставляя туда и . Итак, .

Ответ. 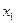=2, =1, =1.

Можно ответ записать и в виде вектора: .

Задача 74. Решить систему уравнений

Решение.

При построении расширенной матрицы, сразу же домножим 2-е и 3-е уравнения на такие коэффициенты, чтобы в начале строки были числа, кратные угловому элементу. А именно, 2-ю строку на 2, а 3-ю строку на 4. Так надо, чтобы потом в методе Гаусса можно было не домножать на дробные коэффициенты при вычитании строк.

Теперь вычтем из 2-й строки 1-ю, домноженную на 3,

а из 3-й строки 1-ю, домноженную на 5.

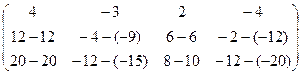Если теперь поменять местами 2 и 3 строки, получится:

система:

И хотя матрица не выглядит как матрица треугольного вида, тем не менее, основная идея метода Гаусса уже реализована: чем ниже, тем меньше переменных, а в последнем уравнении всего одна, а именно . Здесь тоже можно последовательно выразить все переменные, просто начинаем не с последней, а в другом порядке. К треугольному виду в этом случае можно до конца и не приводить.

Итак, из третьего: , то есть .

Подставляем во второе уравнение. , т.е. , .

Из первого: , откуда , .

Ответ. , , .

Задача 75. Решить систему уравнений

Решение. Во-первых, можно всё 2-е уравнение сократить на 2, так удобнее для решения, числа будут меньше. Затем обнуляем ниже углового элемента: вычитаем из 2-го уравнения удвоенное 1-е, а также 3-го 1-е.

треугольная структура уже получилась.

Перепишем снова в виде системы:

из 3-го уравнения , подставляем во 2-е, там получается .

А из 1-го .

Ответ. , , .

Задача 76. Даны 3 вектора: . Доказать, что они образуют базис в пространстве, и найти новые координаты вектора .

Решение. Вычисляя определитель, получим, что он отличен от 0. Затем ищем новые координаты вектора.

система:

Здесь удобнее получить треугольную структуру ниже не главной, а побочной диагонали. Ведь в третьем столбце все числа 1. .

Система: . Из 3-го уравнения .

Тогда из 2-го , а из 1-го уравнения: .

Мы поочерёдно выразили их, начиная с 1-го а не последнего, так как нули ниже побочной, а не главной диагонали. Такая модификация метода Гаусса также возможна.

Ответ. Координаты в новом базисе .

Неопределённые системы ().

Задача 77. Решить неоднородную систему

Решение. Запишем расширенную матрицу, вычтем из 2-й строки 1-ю.

Здесь всего две строки, так что метод Гаусса проводится достаточно коротко.

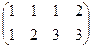
Видим, что базисный минор можно выбрать в первых двух столбцах. Получается, что 3-я переменная свободная. Перепишем снова в виде системы, а не матрицы.

переносим вправо:

Выражаем , а затем поднимаемся в 1-е уравнение и ,через константы и . Впрочем, фактически и так уже выражено:

. Подставим это выражение в 1-е уравнение

, тогда

общее решение системы:

Также записывается в виде вектора: .

Задавая какое-либо значение , всякий раз можем вычислить остальные переменные, и получить тройку чисел. Частные решения: (1,1,0) или (2,-1,1) или (3,-3,2)... их бесконечно много.

Ответ. Общее решение .

Заметим, что разности любых двух частных решений здесь пропорциональны вектору . Вспомните в связи с этим факт, доказанный на лекциях: разность двух частных решений неоднородной системы является решением соответствующей однородной. Теперь можно увидеть это на практике, в конкретных задачах.

Задача 78. Решить систему уравнений .

Решение. Запишем расширенную матрицу и преобразуем её методом Гаусса:

Из 2-й строки отняли 1-ю, из 3-й удвоенную 1-ю. Замечаем, что 2 и 3 строка одинаковы, вычитаем из 3-й 2-ю, и 3-я строка получилась состоящей из 0. Это уравнение 0 = 0, очевидно, его можно вычеркнуть. Базисный минор 2 порядка можно найти в левом верхнем углу. Здесь m = 3, n = 4, r = 2.

Обратите внимание. Типичной и характерной ошибкой является то, что вычёркивают обе пропорциональных строки, а не одну. Но если провести алгоритм Гаусса до конца, то видно, что одна из них остаётся и несёт содержательную информацию, а её копия лишняя, она обратилась в 0. Не нужно торопиться и вычёркивать все пропорциональные строки, ведь хотя бы одна из них не лишняя!

Развернём две оставшихся строки снова в систему уравнений:

Здесь перенесём вправо, 3-я переменная - свободная, базисный минор в левом углу. Замечание. Впрочем, это не единственный вариант: базисный минор можно составить из фрагментов 1 и 3 столбца, тогда была бы свободная. Итак, перенесём :

Основная матрица системы фактически стала квадратной, 2 порядка, т.е. множество коэффициентов при базисных переменных образует такую квадратную матрицу: .

Просто справа при этом не только константы, а составные выражения из констант и каких-то параметров. Видно, что уже и так выражена, . Подставим это выражение в 1-е уравнение, чтобы выразить отдельно через .

в итоге . Итак, - общее решение. В нём есть один свободный параметр .

Его можно записать также и в виде такого вектора: .

Если задавать любое , будет получать тройки чисел, которые служат частными решениями.

Например, при = 1 получим (1,1,1). При = 0 получим (0,3,0). Частных решений бесконечно много.

Ответ. Общее решение .

Задача 79. Решить неоднородную систему

Решение. Построим расширенную матрицу и преобразуем её.

Это равносильно такой системе уравнений

Базисный минор в первых двух столбцах, 3-й столбец соответствует свободной переменной , её надо перенести вправо.

теперь надо выразить через .

фактически и так уже почти выражено, во 2-м уравнении.

. Подставим теперь эту информацию в 1-е уравнение.

, откуда .

Вот эти два выражения ,

как раз и составляют общее решение системы. Задавая любое значение , можно вычислить , и получится конкретная тройка чисел, то есть частное решение.

Общее решение можно записать также в виде такого вектора: .

Частные решения, например:

частное решение .

Ответ. Общее решение .

Задача 80. Решить неоднородную систему

Решение. Запишем расширенную матрицу системы, впрочем, сразу при этом удобно будет поменять местами 1-ю и 3-ю строки, чтобы угловой элемент содержал именно число 1.

обнулим всё ниже углового элемента, для этого:

из 2-й строки вычтем 1-ю, из 3-й удвоенную 1-ю, из 4-й 1-ю, домноженную на 4.

теперь можно поменять местами 2 и 3 строки, а также домножить на три последних уравнения (там почти везде были знаки минус)

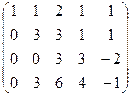
затем из 4-й строки вычитаем 2-ю, чтобы продолжить стандартную процедуру метода Гаусса, потом видим что 3-я и 4-я стали одинаковы, тогда из 4-й вычитаем 3-ю. Получается, что 4-е уравнение 0 = 0.

Итак, осталось 3 уравнения, базисный минор легко заметить в первых трёх столбцах (там треугольная структура матрицы, и этот определитель явно отличен от 0). 4-й столбец не входит в базисный минор, то есть 4-я переменная свободная, т.е. когда будем записывать систему, переносим её через знак равенства во всех уравнениях.