Задача 81. Решить однородную систему:

Решение. Видим, что отличие от предыдущей задачи в том, что справа нулевые константы. Если преобразовывать расширенную матрицу, то получим:



Видим, что справа всё равно как был, так и остаётся столбец из нулей, так что в будущем для однородных систем можно использовать только основную матрицу, ведь расширенная не несёт никакой новой информации, всё равно там справа нулевой столбец, и он не меняется при преобразованиях строк.
Итак, получили систему  базисный минор можно заметить в первых двух столбцах, так что
базисный минор можно заметить в первых двух столбцах, так что  свободная переменная, переносим её вправо:
свободная переменная, переносим её вправо:  . Теперь последовательно выражаем через свободную переменную две базисные переменные.
. Теперь последовательно выражаем через свободную переменную две базисные переменные.
Из 2-го:  , а подставляя в 1-е, получим
, а подставляя в 1-е, получим
 , т.е.
, т.е.  .
.
Общее решение системы:  .
.
Также записывается в виде вектора:  .
.
Отличие от прошлой задачи в том, что на всех местах, где там были константы, здесь 0. Все переменные преобразовывались точно так же.
Частные решения здесь отличаются тем, что задавая  в k раз больше, мы и все остальные получим тоже в k раз больше:
в k раз больше, мы и все остальные получим тоже в k раз больше:
 ,
,  ,
,  ,
,  и так далее.
и так далее.
То есть все тройки чисел будут пропорциональны какой-то одной.
Если для неоднородной системы представить эти тройки чисел как точки в пространстве, то там они образовывали прямую,не проходящую через начало координат, а для однородной системы - проходящую через начало координат. Поэтому разумно выбрать для этой прямой всего 1 вектор, который задаёт её. Это как раз и есть ФСР (фундаментальная система решений). ФСР  .
.
Ответ. Общее решение  , ФСР
, ФСР  .
.
Задача 82. Решить систему 
Решение. Минор, состоящий из 1 и 2 столбцов, уже в треугольной форме. Базисный минор порядка 2. Тогда 3-я и 4-я переменная - свободные. Перенесём их через знак равенства.  .
.
 уже фактически выражено:
уже фактически выражено:  , подставим это в первое уравнение, чтобы выразить
, подставим это в первое уравнение, чтобы выразить  .
.


 .
.
Общее решение: {  ,
,  }.
}.
Если поочерёдно присвоить значение 1 каждой из свободных переменных (а другая в это время 0) то получим гарантированно 2 линейно-независимых вектора, они не пропорциональны, так как 1 на разных местах.
 , получим
, получим 
 , получим
, получим  .
.
Эти 2 вектора {  ,
,  } и есть ФСР. Это
} и есть ФСР. Это  частных решений, из которых можно составить любые другие частные решения: любые их линейные комбинации будут частными решениями однородной системы.
частных решений, из которых можно составить любые другие частные решения: любые их линейные комбинации будут частными решениями однородной системы.
Ответ. Общее решение {  ,
,  }.
}.
ФСР {  ,
,  }.
}.
Замечание. Для системы с квадратной матрицей справа были только числа, для системы с прямоугольной матрицей к ним добавляются свободные переменные, и там будут выражения типа  . А для однородной системы справа констант нет (они = 0), но туда перенесены свободные переменные. То есть идея решения методом Гаусса во всех этих 3 параграфах одна и та же, но справа разные типы объектов.
. А для однородной системы справа констант нет (они = 0), но туда перенесены свободные переменные. То есть идея решения методом Гаусса во всех этих 3 параграфах одна и та же, но справа разные типы объектов.
Задача 83. Решить однородную систему  .
.
Решение. Можно записать основную матрицу и там вычесть 1-ю строку из 2-й, впрочем, можно для небольшой системы сделать это и сразу в системе, вычесть 1-е уравнение из 2-го. Получится:

Ранг равен 2, а неизвестных 3, 3-я неизвестная свободная, переносим вправо. Тогда: 
Из 2-го уравнения  , тогда
, тогда  , а значит
, а значит  .
.
Общее решение:  ,
,  . В виде вектора:
. В виде вектора:  .
.
Присвоим  , получим остальные неизвестные.
, получим остальные неизвестные.
ФСР состоит всего из одного вектора:  . Все остальные решения пропорциональны этому.
. Все остальные решения пропорциональны этому.
Если бы, например, присвоили  , получили бы
, получили бы  . Это потому, что всего одна свободная переменная.
. Это потому, что всего одна свободная переменная.
Ответ. Общее решение:  , ФСР
, ФСР  .
.
Задача 84. Решить однородную систему 
Решение. Запишем основную матрицу, преобразуем её. 


снова представим в виде системы: 
базисный минор порядка 2, можно обвести в левом углу, поэтому 3-я и 4-я переменная - свободные. Здесь их уже две, так как  , поэтому
, поэтому 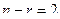 . Перенесём их через знак равенства.
. Перенесём их через знак равенства.

здесь  уже выражено:
уже выражено:  , подставим это в первое уравнение, чтобы выразить и
, подставим это в первое уравнение, чтобы выразить и  .
.
 ,
,  .
.
Общее решение:  ,
,  .
.
В виде вектора:  .
.
Если поочерёдно присвоить значение 1 каждой из свободных переменных (а другая в это время 0) то получим гарантированно 2 линейно-независимых вектора, они не пропорциональны, так как число 1 в них на разных местах.
 , получим
, получим 
 , получим
, получим  .
.
Эти 2 вектора {  ,
,  } и есть ФСР. Это
} и есть ФСР. Это  частных решений, из которых можно составить любые другие частные решения. Любые их линейные комбинации будут частными решениями однородной системы.
частных решений, из которых можно составить любые другие частные решения. Любые их линейные комбинации будут частными решениями однородной системы.
Ответ. Общее решение:  .
.
ФСР это множество из 2 векторов: {  ,
,  }.
}.
Задача 85. Решить однородную систему, найти ФСР. 
Решение. Запишем основную матрицу системы и преобразуем её методом Гаусса.





Ранг матрицы равен 2, базисные столбцы 1-й и 2-й. Несмотря на то, что сначала могло показаться, что здесь будет одна свободная переменная (4 переменных и 3 уравнения), на самом деле здесь будет две свободных переменных, ведь 3-е уравнение оказалось линейной комбинацией первых двух.  .
.
Снова возвращаемся от матрицы к системе уравнений. 
перенесём свободные неизвестные вправо:
 из 2 уравнения
из 2 уравнения  , подставим это в 1-е,
, подставим это в 1-е,
будет  , то есть
, то есть  .
.
Общее решение:  ,
,  .
.
В виде вектора: 
Построим ФСР из 2 векторов.
 , получим
, получим 
 , получим
, получим  .
.
Так как здесь есть дроби, то для того, чтобы векторы в ФСР содержали только целые координаты, можно задавать не только 1, но и другое число, главное только чтобы в 3 и 4 координатах помещался невырожденный минор. Если мы задаём поочерёдно каждой свободной переменной какое-то число (не обязательно 1) а остальным 0, то линейная независимость этой системы векторов всё равно заведомо обеспечена.
Ответ. Общее решение:  ,
,  .
.
ФСР из 2 векторов:  .
.
Задача 86. Решить однородную систему, найти ФСР.

Решение. Преобразуем методом Гаусса основную матрицу системы.





Треугольная структура продолжилась до самой последней строки, и не проявилась строка из нулей, то есть ранг равен 3. Здесь всего одна свободная переменная. Развернём обратно эту матрицу, т.е. запишем в виде системы, а затем перенесём свободные переменные вправо.



Из последнего,  , это подставим во 2-е и получим
, это подставим во 2-е и получим  .
.
Затем это всё в 1-е уравнение, получим  .
.
ФСР: один вектор  .
.
Ответ. Общее решение:  . ФСР:
. ФСР: 
Задача 87. Решить однородную систему, найти ФСР.

Решение. Преобразуем методом Гаусса основную матрицу системы.


 далее можно вычесть 2 строку из 3-й и 4-й, и там везде будут 0.
далее можно вычесть 2 строку из 3-й и 4-й, и там везде будут 0.
Здесь ранг 2, неизвестных 5,  .
.
Переписывая в виде системы, переносим вправо 3 свободных переменных.

Выражаем из 2-го  как линейную функцию от
как линейную функцию от  , а затем с помощью 1-го уравнения, также и
, а затем с помощью 1-го уравнения, также и 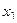 .
.
 ,
,  .
.
Общее решение:  .
.
ФСР из 3 векторов. Для этого задаём поочерёдно 1 какой-либо из свободных переменных, а 0 остальным.
ФСР:  ,
,  ,
,  .
.
Ответ. Общее решение: 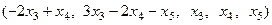 .
.
ФСР:  ,
,  ,
,  .
.
Задача 88. Решить однородную систему, найти ФСР:

Решение. Сначала быстро преобразуем основную матрицу методом Гаусса, для чего из 2 строки вычтем удвоенную 1-ю.


 , видим, что базисный минор в 1 и 2 столбцах, тогда
, видим, что базисный минор в 1 и 2 столбцах, тогда  свободные переменные.
свободные переменные.
Система после преобразования: 
Переносим вправо  :
: 
Последнее уравнение будет логично умножить на коэффициент  .
.
Тогда  , подставляя эту информацию в 1-е уравнение, получим
, подставляя эту информацию в 1-е уравнение, получим  , тогда
, тогда  .
.
Запишем общее решение  ,
,  ,
,
оно же в векторном виде:  .
.
Поочерёдно присваивая  , затем
, затем  , получим два вектора: (-3,5,1,0) и (-5,4,0,1).
, получим два вектора: (-3,5,1,0) и (-5,4,0,1).
Ответ. Общее решение  ,
,  .
.
ФСР (-3,5,1,0) и (-5,4,0,1).
Задача 89. Решить однородную систему, найти ФСР 

Решение. Запишем основную матрицу и преобразуем её:





Третье уравнение было лишнее, ранг основной матрицы равен 2.
Базисные столбца 1-й и 2-й, тогда 3-я переменная свободная.
Система после преобразований: 

Перенесём  :
: 
из 2-го уравнения видно:  , тогда из 1-го уравнения:
, тогда из 1-го уравнения:
 , т.е.
, т.е.  .
.
Общее решение:  ,
,  .
.
Оно же в векторной форме:  .
.
ФСР будет состоять из одного вектора, если 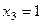 то это
то это  . Впрочем, для того, чтобы все координаты были целыми, можно присвоить
. Впрочем, для того, чтобы все координаты были целыми, можно присвоить  и рассматривать кратный ему вектор
и рассматривать кратный ему вектор  .
.
Ответ. Общее решение:  ,
,  , ФСР:
, ФСР:  .
.
Линейные операторы.
Задача 90. Построить матрицу линейного оператора в 2-мерном пространстве, если действие оператора задано таким образом: 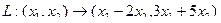 .
.
Решение. Находим, в какие векторы отображаются два базисных вектора:  ,
,  .
.
Эти результаты запишем по столбцам:  .
.
Ответ. Матрица линейного оператора  .
.
Проверка:  . То есть действительно, вычисление координат образа вектора по данным формулам даёт точно такой же результат, как и с помощью умножения на матрицу.
. То есть действительно, вычисление координат образа вектора по данным формулам даёт точно такой же результат, как и с помощью умножения на матрицу.
Так,  но ведь и по исходным формулам
но ведь и по исходным формулам  получилось бы то же самое:
получилось бы то же самое:  .
.
Задача 91. Построить матрицу линейного оператора в 3-мерном пространстве 
Решение. Отобразим базис 3-мерного пространства.



Ответ. Матрица линейного оператора  .
.
Задача 92. С помощью линейного оператора поворота плоскости доказать, что скалярное произведение не изменяется при повороте.
Решение. Рассмотрим векторы  и
и  . Их скалярное произведение равно
. Их скалярное произведение равно  . теперь отобразим каждый из этих векторов с помощью линейного оператора поворота на угол
. теперь отобразим каждый из этих векторов с помощью линейного оператора поворота на угол  .
.

 =
= 

 =
= 
А теперь скалярно перемножим 2 получившихся вектора:
 и
и  .
.
 =
=
 +
+

Учитывая, что 3,4,7,8 слагаемые взаимоуничтожаются, получим:
 =
=  .
.
Ответ: Что и требовалось доказать.
Задача 93. Найти собственные числа и векторы линейного оператора, заданного матрицей:  .
.
Решение. Сначала построим харакреристическое уравнение, то есть отнимем  по главной диагонали, и приравняем этот определитель к нулю.
по главной диагонали, и приравняем этот определитель к нулю.  . Вычислим определитель, чтобы свести всё к уравнению.
. Вычислим определитель, чтобы свести всё к уравнению.  . Характеристические корни
. Характеристические корни  ,
,  .
.
Теперь поочерёдно подставляем каждое конкретное из найденных  , и формируем однородную систему.
, и формируем однородную систему.



 система:
система: 
Здесь есть единственная информация:  . Переменной
. Переменной  в системе нет, но это значит, что она может принимать любое значение, она не влияет на систему уравнений. Распространённая ошибка в данном случае - думать, что если коэффициенты при
в системе нет, но это значит, что она может принимать любое значение, она не влияет на систему уравнений. Распространённая ошибка в данном случае - думать, что если коэффициенты при  нулевые, то
нулевые, то  . На самом деле
. На самом деле  является свободной неизвестной. Если вспомнить тему «ранг матрицы», то увидим, что базисный минор матрицы
является свободной неизвестной. Если вспомнить тему «ранг матрицы», то увидим, что базисный минор матрицы  это минор 1-го порядка, и расположен именно во втором столбце (любая клетка размера 1 на 1), где есть число. Невырожденного минора 2-го порядка здесь нет. Таким образом, 1-я переменная свободная, и пусть даже 2-я через неё здесь не выражена, а просто равна 0, но всё равно свободной переменной мы можем присвоить любое значение, например 1. Итак, ФСР в данном случае (1,0), и именно это и является собственным вектором. Проверка:
это минор 1-го порядка, и расположен именно во втором столбце (любая клетка размера 1 на 1), где есть число. Невырожденного минора 2-го порядка здесь нет. Таким образом, 1-я переменная свободная, и пусть даже 2-я через неё здесь не выражена, а просто равна 0, но всё равно свободной переменной мы можем присвоить любое значение, например 1. Итак, ФСР в данном случае (1,0), и именно это и является собственным вектором. Проверка:  .
.
Замечание. Любой вектор на этой прямой, то есть вида (с,0) тоже является собственным.



 система состоит из одного уравнения:
система состоит из одного уравнения:  . Ранг системы равен 1, а вот базисный минор можно выбрать как в 1-м так и во 2-м столбце, поэтому любую переменную можно считать свободной. Неважно, какую выразить через другую, всё равно одна и та же информация:
. Ранг системы равен 1, а вот базисный минор можно выбрать как в 1-м так и во 2-м столбце, поэтому любую переменную можно считать свободной. Неважно, какую выразить через другую, всё равно одна и та же информация:
 или
или  . Задавая одну, получаем вторую. Вектор (1,1).
. Задавая одну, получаем вторую. Вектор (1,1).
Проверка:  . Действительно, мы нашли такой вектор, который при умножении на эту матрицу становится больше в 3 раза.
. Действительно, мы нашли такой вектор, который при умножении на эту матрицу становится больше в 3 раза.
Ответ.  вектор (1,0),
вектор (1,0),  вектор (1,1).
вектор (1,1).
Задача 94. Найти собственные числа и векторы для матрицы  .
.
Решение. 



 .
.
 . Корни
. Корни  , то есть
, то есть  и 5.
и 5.
Ищем собственный вектор для каждого из этих чисел.




система состоит из двух одинаковых уравнений 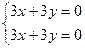
Одну переменную выразим через вторую  . ФСР
. ФСР  .
.




система состоит из пропорциональных уравнений 
Одну переменную выразим через вторую  . ФСР
. ФСР  .
.
Ответ.  вектор
вектор  ,
,  вектор (1,1).
вектор (1,1).
Проверка.  ,
,  .
.
Задача 95. Найти собственные числа и векторы для матрицы  .
.
Решение. 


Здесь хар. корень кратности 2:  .
.
Ищем собственные векторы.



Однородная система состоит всего лишь из одного уравнения  .
.
При этом формально  свободная переменная, так как базисный минор 1-го порядка во втором столбце, а 1-й столбец тогда не базисный. То есть
свободная переменная, так как базисный минор 1-го порядка во втором столбце, а 1-й столбец тогда не базисный. То есть  можно присваивать любое значение, например 1.
можно присваивать любое значение, например 1.
Итак, собственный вектор (1,0). Двух линейно-независимых собственных векторов для этого оператора нет.
Ответ.  , собственный вектор (1,0).
, собственный вектор (1,0).
Замечание. Вообще, количество собственных векторов меньше или равно кратности корня.
А если бы матрица изначально была  то система уравнений получилась бы только из уравнений вида 0 = 0, то есть обе переменные свободные, ФСР было бы (1,0) и (0,1) и тогда собственные векторы - вся плоскость.
то система уравнений получилась бы только из уравнений вида 0 = 0, то есть обе переменные свободные, ФСР было бы (1,0) и (0,1) и тогда собственные векторы - вся плоскость.
Задача 96. Доказать, что линейный оператор  не имеет собственных векторов.
не имеет собственных векторов.
Решение.  .
.
 , действительных корней нет, то есть корни комплексные, они
, действительных корней нет, то есть корни комплексные, они  .
.
Замечание. Если линейный оператор в 3-мерном пространстве, то характеристический многочлен 3 степени, и в том случае есть по крайней мере хотя бы один действительный корень.
Задача 97. Доказать, что для оператора поворота  в общем случае нет собственных векторов, и найти такие углы
в общем случае нет собственных векторов, и найти такие углы  , при которых собственные векторы есть.
, при которых собственные векторы есть.
Решение.  ,
,  ,
,  , получили многочлен вида
, получили многочлен вида  , где
, где
 .
.  .
.
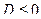 так как
так как 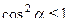 . Лишь для углов 0 и
. Лишь для углов 0 и  получается D = 0, и тогда собственные векторы есть. При
получается D = 0, и тогда собственные векторы есть. При  матрица линейного оператора примет вид
матрица линейного оператора примет вид  , тогда все векторы плоскости являются собственными, и соответствуют числу
, тогда все векторы плоскости являются собственными, и соответствуют числу  .
.
При  матрица
матрица  , все векторы собственные, соответствуют
, все векторы собственные, соответствуют  .
.
Задача 98. Найти собственные числа и векторы 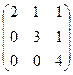 .
.
Решение.  сводится к уравнению
сводится к уравнению
 , корни которого
, корни которого 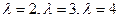 .
.
Найдём собственные векторы.
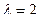 . Вычтем 2 по диагонали, получим систему уравнений
. Вычтем 2 по диагонали, получим систему уравнений
 то есть
то есть  .
.
Из этих уравнений следует, что  , про
, про  нет информации, это свободная переменная. ФСР: вектор (1,0,0).
нет информации, это свободная переменная. ФСР: вектор (1,0,0).
 . Вычтем 3 по диагонали, получим систему уравнений
. Вычтем 3 по диагонали, получим систему уравнений
 то есть
то есть  .
.
Из этих уравнений следует  , ФСР: вектор (1,1,0).
, ФСР: вектор (1,1,0).

Базисный минор здесь во 2 и 3 столбцах, так что  могло считаться свободной переменной.
могло считаться свободной переменной.
 . Вычтем 4 по диагонали, получим систему уравнений
. Вычтем 4 по диагонали, получим систему уравнений
 то есть
то есть  .
.

Базисный минор можно найти, например, в левом верхнем углу, тогда  считаем свободной переменной и все остальные выразим именно через неё. Из 2-го
считаем свободной переменной и все остальные выразим именно через неё. Из 2-го  , а затем из 1-го
, а затем из 1-го  , то есть
, то есть  .
.
ФСР: вектор (1,1,1).
Ответ.
Собст. число  собст. вектор (1,0,0),
собст. вектор (1,0,0),
собст. число  собст. вектор (1,1,0),
собст. вектор (1,1,0),
собст. число  собст. вектор (1,1,1).
собст. вектор (1,1,1).
Задача 99. Найти собственные числа и векторы  .
.
Решение.  сводится к уравнению
сводится к уравнению
 , корни которого:
, корни которого: 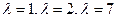 .
.
 .
.
 , система
, система 
откуда  , ФСР это вектор
, ФСР это вектор  .
.
 .
.
 , система
, система 
откуда  , ФСР это вектор
, ФСР это вектор  .
.
 .
.
 , система
, система 
откуда  , а значит и
, а значит и  ,
,  свободная переменная.
свободная переменная.
Тогда ФСР это вектор (1,0,0).
Ответ.
Собст. число  собст. вектор
собст. вектор  ,
,
собст. число  собст. вектор
собст. вектор  ,
,
собст. число  собст. вектор (1,0,0).
собст. вектор (1,0,0).
Задача 100. Найти собственные числа и векторы 
Решение.
 разложим по 2-й строке:
разложим по 2-й строке:
 =
=  что сводится к
что сводится к
 , первый корень и так виден и равен 1, у второго выражения найдём корни, например, через дискриминант, получаем 1 и 2. Итак,
, первый корень и так виден и равен 1, у второго выражения найдём корни, например, через дискриминант, получаем 1 и 2. Итак,  , корни 1,1,2, они же собственные числа. Два характеристических корня совпали (1 это корень кратности 2). Теперь ищем собственные векторы.
, корни 1,1,2, они же собственные числа. Два характеристических корня совпали (1 это корень кратности 2). Теперь ищем собственные векторы.
 .
.
 , если в такой системе уравнений вычесть из 3-го уравнения утроенное 1-е, то 3-е обнулится, и в итоге ранг системы равен 1. То есть мы видим, что в случае корня кратности 2, ранг понизился сразу на 2 пункта, здесь будет 2 свободных неизвестных.
, если в такой системе уравнений вычесть из 3-го уравнения утроенное 1-е, то 3-е обнулится, и в итоге ранг системы равен 1. То есть мы видим, что в случае корня кратности 2, ранг понизился сразу на 2 пункта, здесь будет 2 свободных неизвестных.
Итак, система из 1 уравнения с 3 неизвестными:  .
.
Тогда  , свободные переменные
, свободные переменные  поочерёдно принимают значение 1, ФСР из двух векторов: (1,0,2) (0,1,2).
поочерёдно принимают значение 1, ФСР из двух векторов: (1,0,2) (0,1,2).
 .
.
 , при этом сразу замечаем, что из 2-го уравнения будет следовать
, при этом сразу замечаем, что из 2-го уравнения будет следовать  , поэтому в остальных уравнениях его сразу не пишем. Однородная система:
, поэтому в остальных уравнениях его сразу не пишем. Однородная система:

Ещё два уравнения в ней пропорциональны, так что в итоге, у нас есть такое общее решение:  . ФСР вектор (1,0,3).
. ФСР вектор (1,0,3).
Ответ. Кратный корень  два вектора: (1,0,2) (0,1,2),
два вектора: (1,0,2) (0,1,2),
Корень  вектор (1,0,3).
вектор (1,0,3).
Проверка.  ,
, 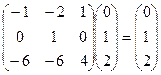 ,
,  .
.
Задача 101. Найти собственные числа и векторы 
Решение. Найдём собственные числа с помощью характеристического уравнения.
 сводится к
сводится к 
Видно, что есть по крайней мере один корень  .
.
Затем разделим многочлен  на
на  , получим крадратичное уравнение и там найдём ещё 2 корня.
, получим крадратичное уравнение и там найдём ещё 2 корня.

Итак, разделилось без остатка. Таким образом,
 =
=  .
.
Для многочлена 2 степени:  . Корни
. Корни  , т.е. 3 и 4.
, т.е. 3 и 4.
Итак, собственные числа:  ,
,  ,
,  .
.
Теперь ищем вектор для каждого из этих чисел.
Пусть  . Составим однородную систему
. Составим однородную систему
 здесь сразу видим, что 2 и 3 строка одинаковы, то есть 3-е уравнение копия 2-го, так что в системе фактически не 3, а 2 уравнения.
здесь сразу видим, что 2 и 3 строка одинаковы, то есть 3-е уравнение копия 2-го, так что в системе фактически не 3, а 2 уравнения.
Запишем систему, заодно при этом поделив 1-е уравнение на 2.

Из 1-го сразу  , подставляя во 2-е, можно также и
, подставляя во 2-е, можно также и  выразить через
выразить через  :
: