Тема. Статистическое изучение вариации
Цель занятия ˗ изучить основные показатели вариации и методику их расчета.
Контрольные вопросы к занятию
| Вопрос | Ответ |
| Что называется вариацией? | |
| Как связаны между собой вариация и типичность средней величины? | |
| На какие группы делятся показатели вариации? | |
| Какие показатели вариации относятся к абсолютным? | |
| Какие показатели вариации относятся к относительным? | |
| В чем назначение показателей вариации? | |
| Какие показатели вариации являются наиболее распространенными? | |
| В чем заключается правило сложения дисперсий? | |
| Какие свойства дисперсии используются для ее расчета по способу моментов? | |
| Как рассчитывается дисперсия альтернативного признака? |
Задание № 1
Заполните пустые ячейки таблицы.
| Показатель вариации | Формула | |
| Для несгруппированных данных | Для сгруппированных данных | |
| Размах вариации | ||
| Среднее линейное отклонение | ||
| Дисперсия | ||
| Среднее квадратическое отклонение | ||
| Коэффициент осцилляции | ||
| Относительное линейное отклонение | ||
| Коэффициент вариации |
Задание № 2
Определить степень вариации средней заработной платы в организации, используя абсолютные и относительные показатели.
| Средняя ЗП, тыс. руб. | Кол-во рабочих, чел. | ||||||
| 3000-4000 | |||||||
| 4000-5000 | |||||||
| 5000-6000 | |||||||
Средняя заработная плата по организации, млн. руб.: 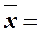
Размах вариации: 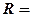
Среднее линейное отклонение: 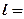
Дисперсия: σ2=
Среднее квадратическое отклонение: σ =
Коэффициент осцилляции: 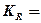
Относительное линейное отклонение: 
Коэффициент вариации: V=
Задание № 3
Определить степень изменения выработки рабочих в бригаде, используя абсолютные и относительные показатели вариации.
| Выработка 1 рабочего, шт. | Кол-во рабочих, чел. | |||||
Решение:
Задание № 4
Определить дисперсию прибыли по группе предприятий всеми известными способами, в т. ч. с использованием её математических свойств.
| Прибыль, млн. руб. | Кол-во предприятий | |||||||||||||
| до 1000 | ||||||||||||||
| 1000-1500 | ||||||||||||||
| 1500-2000 | ||||||||||||||
| 2000 и более | ||||||||||||||
| S |
Средняя прибыль, млн. руб.:
1-й способ:
2-й способ:
3-й способ:
Задание № 5
Определить дисперсию среднемесячной заработной платы работающих по организации всеми известными способами, в т. ч. с использованием её математических свойств.
| ЗП, тыс. руб. | Кол-во человек | |||||||||||||
| до 3000 | ||||||||||||||
| 3000-3500 | ||||||||||||||
| 3500-4000 | ||||||||||||||
| 4000 и более | ||||||||||||||
| S |
Среднемесячная ЗП, тыс. руб.:
1-й способ:
2-й способ:
3-й способ:
Задание № 6
Решите примеры.
| Задание | Ответ |
| Чему равен размах вариации? X: 30; 10; 15; 25; 70; 85 | |
| Чему равен размах вариации? X: 1; 2,7; 8; 12; 20; 21 | |
| Чему равна дисперсия, если среднее квадратическое отклонение равно 5, а среднее значение признака 2? | |
| Чему равно среднее квадратическое отклонение, если дисперсия равна 16, а среднее значение признака 2? | |
| Размах вариации равен 80, средняя величина признака равна 8. Рассчитайте коэффициент осцилляции. | |
| Коэффициент осцилляции равен 8, средняя величина признака равна 4. Рассчитайте размах вариации. | |
| Среднее линейное отклонение равно 25, средняя величина признака равна 5. Рассчитайте относительное линейное отклонение. | |
| Относительное линейное отклонение равно 4, средняя величина признака равна 9. Рассчитайте среднее линейное отклонение. | |
| Чему равен коэффициент осцилляции, если размах вариации равен 5, среднее квадратическое отклонение равно 1, а среднее значение признака 5? | |
| Чему равно относительное линейное отклонение, если среднее линейное отклонение равно 15, дисперсия равна 25, а среднее значение признака 10? | |
| Чему равен коэффициент вариации, если среднее квадратическое отклонение равно 2, а среднее значение признака 10? | |
| Среднее квадратическое отклонение равно 10, средняя величина признака равна 4. Рассчитайте коэффициент вариации. | |
| Коэффициент вариации равен 10, средняя величина признака равна 6. Рассчитайте среднее квадратическое отклонение. | |
| Коэффициент вариации равен 10, средняя величина признака равна 6. Рассчитайте дисперсию. | |
| Дисперсия признака равна 2. Все значения признака увеличились в 2 раза. Чему будет равна дисперсия? | |
| Дисперсия признака была равна 27. Все значения признака уменьшились в 3 раза. Чему будет равна дисперсия? | |
| Если в представленном ряду (Х: 45, 65, 85, 95, 105) все значения признака увеличить на число X0 = 10, как изменится дисперсия? | |
| Если в представленном ряду (Х: 90, 120, 150, 180, 210, 240) все значения признака уменьшить на число X0 =25, как изменится дисперсия? | |
| Если представленные частоты ряда (f=2, 5, 3, 4, 2) увеличить в 2 раза, как изменится дисперсия? | |
| Если представленные частоты ряда (f=2, 4, 8, 10, 6) уменьшить в 2 раза, как изменится дисперсия? |
Задание № 7
Имеются следующие данные о товарообороте двух магазинов
| Номер магазина | Среднедневной товарооборот, млн. руб. | Дисперсия среднедневного товарооборота | Коэффициент вариации, % |
Определить:
1) в каком магазине и на сколько процентов выше товарооборот.
2) в каком магазине выше вариация товарооборота.
Задание № 8
Имеются данные о распределении рабочих двух бригад, работающих по разным технологиям, по уровню производительности труда в млн. руб.
Бригада № 1 (6 чел.):130, 145, 155, 160, 170, 180.
Бригада № 2 (8 чел.): 260, 240, 170, 200, 150, 210, 220, 230.
Определить:
1) средний уровень производительности труда по каждой бригаде;
2) общую дисперсию уровня производительности труда по двум бригадам;
3) внутригрупповые дисперсии производительности труда;
4) межгрупповую дисперсию;
5) проверить правило сложения дисперсий.
1. Средний уровень производительности труда:
· по бригаде № 1
· по бригаде № 2
· по двум бригадам
2. Общая дисперсия уровня производительности труда по двум бригадам:
3. Внутригрупповая дисперсия производительности труда:
· по бригаде № 1
· по бригаде № 2
Средняя из внутригрупповых дисперсий:
| Производительность труда, млн. руб. | ||||
| бригада № 1 | ||||
| Итого по бригаде № 1 | ||||
| бригада № 2 | ||||
| Итого по бригаде № 2 | ||||
| Итого по двум бригадам |
4. Межгрупповая дисперсия
| Средняя производительность труда по бригаде, млн. руб. | Число рабочих в бригаде, чел. | |||
| S |
5. Проверка правила сложения дисперсий:
Задание № 9
1. По результатам проверки качества продукции определено, что 240 единиц соответствуют стандарту, а 30 – не соответствуют. Определить дисперсию доли нестандартной продукции.
2. Зимнюю экзаменационную сессию 20 студентов группы сдали успешно, а 5 имели академическую задолженность. Определить дисперсию доли студентов, успешно сдавших сессию.