Тема. Выборочное наблюдение
Цель занятия ˗ освоить методологию проведения выборочного наблюдения и научиться рассчитывать характеристики выборочной совокупности.
Контрольные вопросы к занятию
| Вопрос | Ответ |
| Какой вид наблюдения называется выборочным? | |
| В чем заключается основная цель выборочного наблюдения? | |
| Перечислите правила отбора единиц из генеральной в выборочную совокупность. | · · · |
| В чем заключаются преимущества выборочного наблюдения по сравнению со сплошным? | |
| Перечислите основные этапы выборочного наблюдения. | · · · · · |
| Что называют ошибками выборочного наблюдения? | |
| Почему ошибки выборочного наблюдения называют средними? | |
| Для чего применяются предельные ошибки выборочного наблюдения? | |
| Что показывает коэффициент доверия t при расчете предельных ошибок выборочного наблюдения? | |
| Какая выборка называется малой? |
Задание № 1
Заполните пустые ячейки таблицы.
Характеристики генеральной и выборочной совокупности
| Показатели | Совокупность | |
| генеральная | выборочная | |
| N | ||
| Среднее значение признака | ||
| m | ||
| Доля единиц, обладающих изучаемым признаком | ||
| 1-p (q) | ||
| Дисперсия | ||
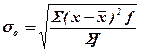
|
Задание № 2
Заполните пустые ячейки схемы классификации видов, способов и методов отбора единиц в выборочную совокупность.
           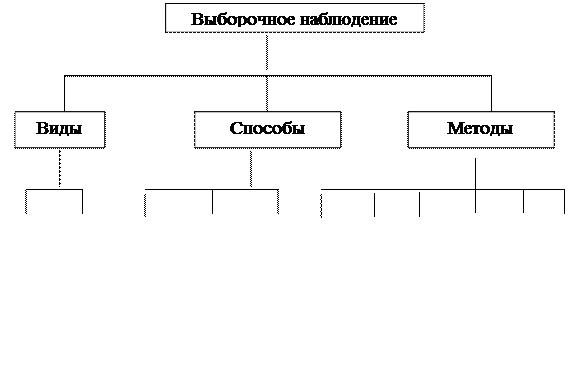 |
Задание № 3
Соедините стрелками соответствующий метод отбора и его характеристику.
| ||||||
 | ||||||
| ||||||
 | ||||||
| ||||||
| ||||||
| ||||||
| ||||||
| ||||||
Задание № 4
|
 | |||
 | |||
 | |||
| |||
| |||
Задание № 5
Заполните таблицу для расчета средних ошибок выборки для различных видов и методов отбора.
| Метод отбора | Вид отбора | |||
| Повторный | Бесповторный | |||
| Для средней | Для доли | Для средней | Для доли | |
| Случайный и механический | 
| 
| ||
| Типический | 
| |||
| Серийный | 
| 
|
Алгоритм решения задач по расчету ошибки выборочного наблюдения:
1. Определяем, о чем в задаче идет речь – о средней или о доле?
2. Определяем вид и метод отбора.
3. Находим формулу для расчета средней ошибки выборки.
4. Определяем необходимые показатели для расчета средней ошибки.
5. Рассчитываем среднюю ошибку выборки.
6. Рассчитываем предельную ошибку выборки в соответствии с доверительной вероятностью.
7. Рассчитываем пределы нахождения генеральной средней или доли.
Задание № 6
Из 20000 изделий для проверки массы методом случайной повторной выборки было отобрано 200 изделий. Средний вес изделия по результатам выборки составил 30 г. Значение среднего квадратичного отклонения составило 4. Необходимо определить:
1) с вероятностью 0,954 определить пределы, в которых находится средний вес изделия в генеральной совокупности;
2) как изменятся пределы, в которых находится средняя по генеральной совокупности, если вероятность будет равна 0,997?


Задание № 7
В цеху работает 2450 ткачей. Для определения среднего объема производства ткани в час была организована 4 %-ная случайная бесповторная выборка ткачей. По ее результатам было получено следующее распределение ткачей по выработке ткани в час:
| Выработка ткани, пог. м. | Число ткачей | ||||
| 2-6 | |||||
| 6-10 | |||||
| 10-14 | |||||
| 14-18 | |||||
| 18-22 | |||||
| 22-26 | |||||
С вероятностью 0,954 найдите пределы, в которых будет находиться средняя выработка ткани в генеральной совокупности.
Задание № 8
В городе проживает 250 тыс. семей. Для определения среднего числа детей в семье была организована 2 %-я бесповторная выборка семей. По ее результатам было получено следующее распределение семей по числу детей:
| Число детей в семье | Количество семей | |||
С вероятностью P=0,954 найти пределы, в которых будет находиться среднее число детей в семье по генеральной совокупности.
Задание № 9
При контрольной проверке качества электроламп была проведена серийная выборка. Из партии, содержащей 100 коробок с лампами, было выбрано 5 механическим методом. В результате сплошного обследования находящихся в коробках ламп получены данные о проценте бракованных ламп, которые составили соответственно 3 %, 1,05 %, 2,01 %, 4,0 %, 0,6 %. С вероятностью 0,683 найдите средний процент бракованных ламп в партии.
Задание № 10
С целью определения средней фактической продолжительности рабочего дня в государственном учреждении с численностью служащих 480 человек была проведена 25 %-ная механическая выборка. По результатам наблюдения оказалось, что у 10 % обследованных потери рабочего времени достигали более 45 минут в день. С вероятностью 0,997 установите пределы, в которых находится генеральная доля служащих с потерями рабочего времени более 45 минут в день.
Задание № 11
С целью определения среднего размера вклада в отделениях сбербанка города предполагается провести механическую бесповторную выборку лицевых счетов из общего их числа 67800. По данным предыдущего обследования установлено, что среднее квадратическое отклонение размера вклада равно 14000 рублей. С вероятностью 0,997 определите необходимый объём выборочной совокупности при условии, что ошибка выборки не должна превышать 1000 рублей.
Задание № 12
В ОАО «Омега» 200 бригад рабочих. Планируется проведение выборочного обследования с целью определения удельного веса рабочих, имеющих профессиональные заболевания. Дисперсия доли рабочих, имеющих профессиональные заболевания по результатам пробного обследования, равна 225. С вероятностью 0,954 рассчитайте необходимое для выборки количество бригад, если ошибка выборки не должна превышать 5 %.
Задание № 13
С целью определения средних затрат времени при поездках на работу населения города численностью 350000 человек планируется провести выборочное наблюдение на основе случайного повторного отбора. Сколько людей должно быть обследовано, чтобы с вероятностью 0,954 ошибка выборочной средней не превышала 1 минуту при среднем квадратическом отклонении 15 минут.