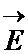Тема 2. Свойства твердофазных дисперсных систем,
Их устойчивость и коагуляция
Оптические свойства твердофазных дисперсных систем
Л е к ц и я
Саратов – 2013
СОДЕРЖАНИЕ
Введение
1. Процессы рассеяния света золями.
2. Процессы поглощения света золями.
3. Оптические методы исследования дисперсных систем.
Заключение
ЛИТЕРАТУРА
основная
1. Щукин Е.Д., Перцов А.В., Амелина Е.А. Коллоидная химия. – М.: Высш. шк., 2006. – С. 208 – 218, 228 – 229.
2. Гельфман М., Ковалевич О., Юстратов В. Коллоидная химия. – СПб.: «Лань», 2003. – С. 89 - 100.
НАГЛЯДНЫЕ ПОСОБИЯ И ПРИЛОЖЕНИЯ
1. Слайды 21 – 25:
«Рассеяние света золями»
«Поглощение света золями»
«Схема ультрамикроскопа и нефелометра»
«Эффект Тиндаля»
2. Опыт «Эффект Тиндаля»
3. Презентация лекции в программе «Power Point»
ВВЕДЕНИЕ
Оптические свойства гетерогенных систем резко отличаются как от свойств истинных растворов, так и от свойств грубодисперсных систем. Эти отличия связаны с тем, что размеры частиц дисперсной фазы соизмеримы с длиной волны падающего на систему видимого света.
При падении луча света на дисперсную систему могут наблюдаться следующие явления:
прохождение света через систему;
преломление света частицами дисперсной фазы;
отражение света частицами дисперсной фазы;
рассеяние света (это явление проявляется в виде опалесценции);
абсорбция (поглощение) света дисперсной фазой с превращением световой энергии в тепловую.
Прохождение света характерно для прозрачных систем молекулярной или ионной степени дисперсности (газы, большинство индивидуальных жидкостей и истинных растворов, аморфные и кристаллические тела). Преломление и отражение света всегда наблюдается у микрогетерогенных систем и находит свое выражение в мутности относительно грубых суспензий и эмульсий, наблюдаемой как в проходящем (прямом), так и отраженном (боковом свете).
Для гетерогенных систем из всех возможных оптических явлений наиболее характерны рассеяние и поглощение света.
Важность изучения оптических свойств дисперсных систем трудно переоценить. Ввиду того, что взвеси твердых частиц в морской и речной водах являются коллоидными и микрогетерогенными системами. Оптика твердофазных дисперсных систем имеет непосредственное отношение к фотографированию с помощью инфракрасных лучей, использованию разнообразных аэрозолей в качестве дымовых завес, а также к применению светомаскировки и светосигнализации.
Изучение особенностей прохождения света через дисперсные системы лежит в основе оптических методов исследования дисперсных систем, которые позволяют изучать их структуру, определять размеры и форму частиц дисперсной фазы, а также их концентрацию. При этом оптические методы исследования охватывают широкую область дисперсности, что позволяет изучать частицы, не видимые в обычный микроскоп. Ультрамикроскопические наблюдения способствовали детальному изучению таких явлений, как диффузия, броуновское движение, седиментация, коагуляция.
Таким образом, целью настоящей лекции является рассмотрение физических основ наиболее характерных оптических свойств дисперсных систем – рассеяния и поглощения света золями, а также рассмотрение оптических методов исследования дисперсных систем.
Рассеяние света золями
Рассеяние света мелкими частицами было описано еще Ломоносовым. Подробно его изучали М. Фарадей и Дж. Тиндаль. Если мы направим луч света на истинный и коллоидный раствор, то мы будем наблюдать совершенно разные картины. В истинном растворе путь луча незаметен, в то время как прозрачная на вид гетерогенная система в лучах света опалесцирует – освещенный участок системы светится, образуя след луча (рисунок 1). Это явление, получившее название эффекта Тиндаля (Фарадея – Тиндаля, конус Тиндаля), есть специфическое свойство гетерогенных систем.
Таким образом, эффект Тиндаля – это явление свечения (опалесценции) луча света в коллоидных растворах.
Это явление используется для идентификации гетерогенных систем; направляя луч на испытуемый раствор, можно определить, является ли этот раствор истинным или коллоидным. (Демонстрация опыта с лучом света, направленным на сосуд с дистиллированной водой и с коллоидным раствором). Этот прием можно использовать для обнаружения взвешенных частиц в питьевой воде.
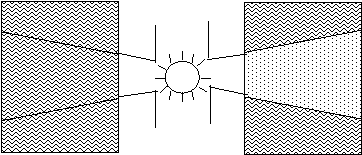
Истинный раствор Гетерогенная система
Рис. 1. Эффект Тиндаля
Причиной эффекта Тиндаля является рассеяние света.
Рассеяние – такое взаимодействие света с веществом, в результате которого световая энергия переизлучается (рассеивается) в окружающее пространство.
Явление рассеяния света наблюдается только в неоднородных системах. В дисперсной системе в качестве такой неоднородности выступает частица дисперсной фазы. Рассмотрим, что происходит в частице под действием света. Как известно, свет является поперечной электромагнитной волной, в которой происходят колебания вектора электрической напряженности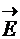 
(рисунок 2). Все электроны частицы попадают в электрическое поле волны, которое периодически меняет свое направление. Если частица мала по сравнению
| |||
 | |||
Рис.2. Частица в электромагнитной световой волне
с длиной световой волны, то все её электроны колеблются в одной фазе, возникает индуцированный электрический диполь, который излучает электромагнитные волны, частота которых совпадает с частотой падающего света. Возникает рассеянный свет, который распространяется во всех направлениях.
Теория светорассеяния (опалесценции) для сферических, не поглощающих света частиц, была разработана Релеем на основании законов классической электродинамики.
Эта теория справедлива при выполнении следующих условий:
1. Рассеивающие частицы малы, их размер меньше 0,1 длины волны падающего света (а < l/10). При этом колебание зарядов в частице происходит в одной фазе. Поскольку белый свет содержит волны с длиной волны 400-700 нм, постольку размер частиц должен быть менее 40-70 нм. Форма частиц - сферическая.
2. Частицы не поглощают света (не окрашены).
3. Частицы неэлектропроводны (диэлектрики).
4. Концентрация частиц мала – расстояние между частицами велико по сравнению с длиной волны падающего света (в этом случае свет не интерферирует).
5. Объем дисперсной системы, через который проходит рассеянный свет, мал, и можно не учитывать вторичное рассеяние рассеянного света.
При выполнении этих условий интенсивность света рассеянного единицей объема дисперсной фазы подчиняется уравнению Релея:
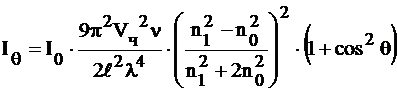(1)
где I0 – интенсивность падающего света;
Iq – интенсивность света, рассеянного под углом q к направлению падающего светового потока (интенсивность света – энергия, переносимая светом за единицу времени через единицу поверхности, перпендикулярной направлению его распространения).
Vч – объем одной частицы;
n – концентрация частиц;
l – расстояние от центра рассеивающего объема до наблюдателя;
l – длина волны падающего света;
n0, n1 – показатели преломления дисперсионной среды и дисперсной
фазы соответственно;
q – угол между направлением падающего светового потока и рас сеянного света.
Таким образом, величина интенсивности рассеянного света зависит от многих факторов.
Сумму всего рассеянного частицами света R можно вычислить путем интегрирования уравнения (1) по поверхности сферы, поскольку свет рассеивается по всем направлениям. В результате получается:
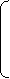
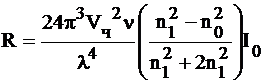= t . Iq (2)
Выражение в квадратных скобках представляет собой величину
t -мутность системы, которая указывает на убыль световой энергии из проходящего потока света в результате его рассеяния по всем направлениям. В уравнении (2) отсутствует величина l, поскольку общее количество рассеянного света не зависит от расстояния от источника рассеяния.
Уравнение Релея содержит много переменных. Проведем анализ уравнения Релея, то есть рассмотрим влияние отдельных факторов на рассеяние света.
1. Зависимость интенсивности рассеянного света Iqот направления (от угла q).
Iq ~ (1+Cos2q)
В соответствии с уравнением Релея интенсивность рассеянного света пропорциональна величине (1+Cos2q), поэтому интенсивность рассеянного света в разных направлениях различна. Больше всего света рассеивается под углом в 00 и 1800 к лучу, падающему на частицу, т.е. по направлению луча и в противоположном направлении (Cos2q = 1). Минимум рассеяния наблюдается под углом 900 к направлению падающего луча (Cos2q = 0). При этом свет, рассеянный под углом 900, является поляризованным, а рассеянный под углом 00 и 1800 поляризован частично.
Картину рассеяния света удобно представлять в виде векторной диаграммы, предложенной Ми. Такую диаграмму называют индикатрисой рассеяния. Для получения такой диаграммы от точки, изображающей частицу откладывают во всех направлениях интенсивность света (выраженную в каких-либо единицах) в виде радиусов-векторов, в любой плоскости, содержащей ось Х (направление падающего светового луча), и концы векторов соединяют непрерывной линией. Диаграмма Ми приведена на рисунке 3.
Рис.3. Рассеяние света сферической частицей (Диаграмма Ми, индикатриса рассеяния)
Приведенная диаграмма относится к рассеянию света сферическими частицами. Для частиц большего размера и другой формы индикатриса имеет другой вид.
2. Зависимость Iq от концентрации частиц.
Если дисперсные системы отличаются только концентрацией частиц, а все остальные параметры постоянны (радиус частиц, длина волны падающего света, показатели преломления), то интенсивность рассеянного света будет пропорциональна концентрации частиц n:
Iq ~ n или Iq= К .n,
где К – константа, включающая все неизменные в данном опыте величины в уравнении Релея.
Чем больше концентрация частиц, тем больше интенсивность рассеянного света. Эту зависимость можно использовать в аналитической химии для определения концентрации частиц дисперсной фазы. Метод, основанный на применении этой зависимости, называется нефелометрия. Его мы подробно рассмотрим в третьем учебном вопросе.
3. Зависимость Iq от размера частиц.
Iq ~ V2 (~ r6)
Интенсивность рассеянного света пропорциональна квадрату объема частицы, то есть для сферических частиц - шестой степени их радиуса. Уменьшение размера частицы ведет к соответствующему уменьшению светорассеяния.
Опалесценция истинных растворов весьма незначительна, так как вследствие малого объема частиц (молекул) выражение V2 в числителе уравнения Релея очень невелико. Светорассеяние в этих случаях может наблюдаться при применении лучей с малой длиной волны, например, рентгеновских лучей (длина волны рентгеновских лучей 0,04-0,06 нм).
При увеличении частиц до размера, значительно превышающего длину световой волны, светорассеяние переходит в отражение света и интенсивность рассеянного света уменьшается. Поэтому максимальным светорассеянием обладают коллоидные системы.
4. Зависимость Iq от длины волны.
Интенсивность рассеянного света Iq обратно пропорциональна четвертой степени длины волны:
Iq ~ 1/l4
Как известно, белый свет включает волны с различной длиной (таблица 1).
Таблица 1 - Спектральные цвета волн видимой части спектра
| Длины волн, нм | Цвет световых лучей (поглощаемые лучи) | Дополнительные цвета (окраска раствора) |
| 400 - 435 | фиолетовый | зеленовато-желтый |
| 435 - 480 | синий | желтый |
| 480 -500 | сине-зеленый | оранжево-красный |
| 500- 560 | зеленый | пурпурный |
| 560 -580 | желтовато-зеленый | фиолетовый |
| 580 -595 | желтый | синий |
| 595 -730 | оранжево - красный | сине-зеленый |
| 730 -760 | пурпурный | зеленый |
Если на кювету с коллоидным раствором направить белый свет, то лучи с разной длиной волны будут рассеиваться по-разному (рисунок 4).
 |
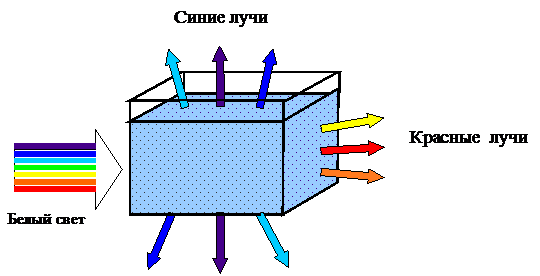Рис. 4. Рассеяние лучей с разной длиной волны
Красный и оранжевый свет имеют наибольшую (600 – 760 нм) длину волны видимой части спектра и поэтому рассеиваются в меньшей степени, они как бы проходят через раствор. Наименьшую длину волны имеет синий и фиолетовый свет (длина волны 380 – 450 нм), эти лучи рассеиваются в большей степени. Эти явления являются причиной того, что бесцветные коллоидные системы под действием белого света при боковом освещении обнаруживают синеватую окраску, а в проходящем свете окрашены в желто-оранжевый цвет. Из падающего на дисперсную систему белого света рассеиваются главным образом короткие (сине-фиолетовые) волны (их видно сбоку), а красно-оранжевые проходят через раствор. По этой причине запрещающие сигналы светофоров имеют красный свет, который виден на больших расстояниях, поскольку мало рассеивается. Оранжевая окраска защитных жилетов дорожных рабочих также обусловлена малым рассеиванием лучей оранжевого цвета. И, наоборот, при светомаскировке необходимо применять лампы синего и фиолетового цвета. Значительное рассеяние света этих ламп исключает возможность увидеть объект даже на небольшом расстоянии.
Следует заметить, что преимущественное рассеяние света с малой длиной волны объясняет цвет неба в различное время дня, а также цвет морской волны. Причина голубого цвета неба заключается в рассеивании коротких волн солнечного света атмосферой Земли. Оранжевый или красный цвет неба при восходе или заходе Солнца объясняется тем, что утром или вечером наблюдается свет, прошедший через атмосферу, а не рассеянный.
5. Зависимость Iq от показателей преломления дисперсной фазы и дисперсионной среды.
Iq ~ (n12 – n02)
Уравнение (1) показывает, что, чем больше разность показателей преломления дисперсной фазы и дисперсионной среды, тем больше рассеяние. Например, очень высокое рассеяние наблюдается в металлических золях и, наоборот, низкое в растворах полимеров. Бывают случаи, когда дисперсные системы вовсе не рассеивают свет из-за равенства показателей преломления дисперсной фазы и дисперсионной среды. В этом случае может создаться ошибочное впечатление, что мы имеем дело с истинным раствором, а не с коллоидным.
Итак, мы рассмотрели основные факторы, влияющие на рассеяние света дисперсными системами, подчиняющимися уравнению Релея.
Отклонения от уравнения Релея связаны, в основном, с увеличением размера частиц до величины, превышающей 0,1 l - длины световой волны.
Так, например, индикатриса рассеяния для крупных частиц имеет форму несимметричной восьмерки, вытянутой в направлении падающего света.
Наиболее важным с практической точки зрения является отклонение от уравнения Релея, связанное с изменением показателя степени у длины волны. Его величина становится меньше 4.
Для частиц с размером больше 0,1l зависимость светорассеяния от длины волны описывается уравнением Геллера:
R = k . l-x или t = k¢. l-x, (3)
поскольку R ~ t (уравнение 2).
Значения х могут меняться от 4 до 1 в зависимости от радиуса частиц и от соотношения показателей преломления дисперсной фазы и дисперсионной среды. Определив экспериментально показатель степени, можно рассчитать размер частиц дисперсной фазы. На использовании зависимости (3) основан метод спектра мутности, которыйприменяетсядля определения размера частиц. С этим методом мы будем знакомиться на лабораторной работе и использовать его для определения размера частиц дисперсной фазы.
Теперь перейдем к рассмотрению явления поглощения света коллоидными растворами.
ПОГЛОЩЕНИЕ СВЕТА ЗОЛЯМИ
В коллоидных растворах наблюдаются явления истинного и «кажущегося» поглощения света. Разберемся с этими понятиями.
Рассмотрим три возможных случая.
Поглощение света истинным окрашенным раствором
Рассмотрим прямоугольную кювету длиною l, в которую помещен истинный раствор, обладающий окраской (рисунок 5). Если на него направить монохроматическое излучение с определенной длиной волны и интенсивностью I0, то при прохождении через раствор часть света поглотится окрашенными молекулами растворенного вещества, энергия излучения перейдет в тепловую энергию. На выходе из кюветы интенсивность света будет меньше (I).
I
Рис. 5. Поглощение света истинным окрашенным раствором
Поглощение света описывается законом Бугера-Ламберта-Бера в экспоненциальной форме:
I = I0 . е–Кl (4)
где I – интенсивность света, прошедшего через дисперсную систему;
I0 – интенсивность света, падающего на дисперсную систему;
К – показатель поглощения;
l – длина светового пути в растворе.
Этот закон справедлив для истинных растворов. С этим законом мы знакомились в курсе аналитической химии.
2. Кажущееся поглощение света бесцветными золями
Если в кювету поместить бесцветный коллоидный раствор, то окажется, что интенсивность света на выходе тоже будет меньше, но это произойдет за счет частичного рассеяния света. Такое рассеяние света называется "кажущимся поглощением" (рисунок 6).
 |
Рис. 6. Поглощение света бесцветным (белым) золем
В этом случае " кажущееся поглощение " также можно описать уравнением Бугера-Ламберта-Бера, но в этом случае оно примет вид:
I = I0 . е-tl, (5)
где t - мутность системы или показатель рассеяния (см. уравнение 2).
3. Поглощение света окрашенными золями
Если же частицы золя имеют собственную окраску, то в таких системах одновременно наблюдаются и рассеяние света и поглощения света частицами. В случае одновременного поглощения и рассеяния света уравнение Бугера-Ламберта-Бера (4) примет вид:
I = I0 . е-Сl, (6)
где С = t + К – показатель ослабления света или коэффициент
экстинкции.
Таким образом, мы рассмотрели три уравнения, характеризующие поглощение света различыми системами. Они отличаются показателями степени. Однако, все три показателя степени С, t, К (коэффициент экстинкции, мутность, показатель поглощения) зависят от концентрации частиц в золе. Последнее уравнение является обобщенным и имеет универсальный характер. После его логарифмирования и некоторых преобразований получают обобщенное выражение для закона Бугера – Ламберта –Бера:
A = k × сзоля × l (7)
Где A = lg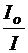 
- оптическая плотность раствора,
сзоля – концентрация золя,
l – длина кюветы,
k – коэффициент, учитывающий и поглощение и рассеяние света.
Для истинных растворов k = e – молярный коэффициент поглощения.
Как вам хорошо известно, оптическую плотность растворов легко измерить с помощью любого фотометра типа КФК-2 или КФК-3. Поэтому это уравнение легко использовать для определения концентрации частиц дисперсной фазы (например, применяя метод градуировочного графика).
Между мутностью t и оптической плотностью A существует простая связь:
t =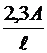 
(8)
Таким образом, измерив оптическую плотность А, можно вычислить мутность системы t, а по величине t можно определить размер частиц (см. уравнение 2).
Надо отметить, что окрашенные золи обладают интенсивной окраской (окраска усиливается за счет многократного рассеяния). Например, цвет драгоценных и полудрагоценных камней обусловлен присутствием в них ничтожных количеств тяжелых металлов и их оксидов в коллоидной степени дисперсности. Особенно интенсивно окрашены золи металлов. Это объясняется двумя причинами. С одной стороны, такие золи сильно рассеивают свет, поскольку велика разность показателей преломления металлических частиц и дисперсионной среды. С другой стороны, в частице, проводящей электричество, электромагнитное поле световой волны индуцирует электродвижущую силу. Электрическая энергия переходит в тепловую. Короткие электромагнитные волны (от 100 до 1000 нм) практически полностью поглощаются.
На окраску гетерогенных систем влияет также дисперсность частиц. Золи одного и того же металла могут иметь разнообразную окраску. Так, грубодисперсные золи золота обычно имеют голубой цвет (в проходящем свете) и опалесцируют красным цветом (в рассеянном свете). Высокодисперсные золи золота, наоборот, обычно окрашены в красный цвет и опалесцируют голубым цветом. Интересно, что при еще большей степени дисперсности золи золота приобретают сначала зеленый, а затем желтый цвет.