Для определения параметров уравнения регрессии применяют метод наименьших квадратов (МНК). Метод был предложен К. Гауссом (1777 – 1855) и А. М. Лежандром (1752 – 1833) независимо друг от друга.
Сущность метода наименьших квадратов заключается в том, что отыскиваются такие значения параметров уравнения регрессии, при которых сумма квадратов отклонений фактических значений результативного признака от теоретических будет наименьшей из всех возможных, т.е.
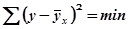 , (8.5)
, (8.5)
где у – фактические значения результативного признака;
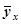 – теоретические значения результативного признака.
– теоретические значения результативного признака.
Для нахождения минимума функции следует приравнять к нулю частные производные по 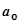 и
и 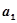 :
:
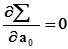 и
и  . (8.6)
. (8.6)
Рассмотрим, как определяются параметры уравнения регрессии для различных видов аналитических функций.
1. Уравнение прямой:
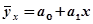 , (8.7)
, (8.7)
где 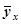 – теоретическое значение результативного признака;
– теоретическое значение результативного признака;
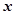 –значениефакторного признака;
–значениефакторного признака;
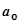 и
и 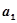 –параметры уравнения прямой;
–параметры уравнения прямой;
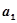 –коэффициент регрессии(пропорциональности), характеризующий изменение среднего значения результативного признака при изменении факторного признака на единицу собственного измерения.
–коэффициент регрессии(пропорциональности), характеризующий изменение среднего значения результативного признака при изменении факторного признака на единицу собственного измерения.
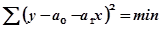 , (8.8)
, (8.8)
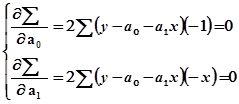 (8.9)
(8.9)
После преобразования получим систему нормальных уравнений:
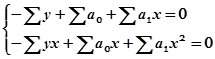 (8.10)
(8.10)
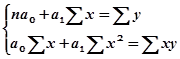 (8.11)
(8.11)
где n – число пар взаимосвязанных признаков.
По эмпирическим данным необходимо рассчитать все приведенные в формулах суммы и подставив их в систему уравнений, найти параметры искомой прямой.
Систему можно решить методом определителей:
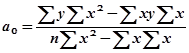 ; (8.12)
; (8.12)
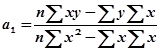 ; (8.13)
; (8.13)
 . (8.14)
. (8.14)
Значения параметров 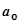 и
и 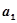 подставляют в уравнение регрессии и находят теоретические значения результативного признака, которые показывают, каким теоретически должен быть средний размер результативного признака при данном размере факторного признака.
подставляют в уравнение регрессии и находят теоретические значения результативного признака, которые показывают, каким теоретически должен быть средний размер результативного признака при данном размере факторного признака.
Пример 8.1. Построим линейное уравнение регрессии по данным табл. 8.1 и определим зависимость объема продукции от стоимости основных производственных фондов.
Таблица 8.1
Расчетная таблица для определения параметров
Линейного уравнения регрессии
| Номер пред-приятия | Объем продукции,
млн. руб.
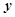
| Стоимость основных производственных фондов,
млн. руб.
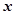
|

|
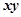
|
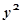
|
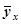
|
| 12,0 | 4,5 | 20,25 | 54,00 | 144,00 | 12,48 | |
| 12,7 | 4,7 | 22,09 | 59,69 | 161,29 | 12,71 | |
| 13,2 | 4,9 | 24,01 | 64,68 | 174,24 | 12,94 | |
| 14,0 | 5,2 | 27,04 | 72,80 | 196,00 | 13,29 | |
| 13,8 | 6,0 | 36,00 | 82,80 | 190,44 | 14,23 | |
| 15,0 | 6,5 | 42,25 | 97,50 | 225,00 | 14,81 | |
| 15,5 | 6,8 | 46,24 | 105,40 | 240,25 | 15,16 | |
| 14,8 | 7,2 | 51,84 | 106,56 | 219,04 | 15,62 | |
| 16,4 | 7,9 | 62,41 | 129,56 | 268,96 | 16,44 | |
| 18,0 | 9,0 | 81,00 | 162,00 | 324,00 | 17,72 | |
| Итого | 145,4 | 62,7 | 413,13 | 934,99 | 2143,22 | 145,4 |
1. Линейное уравнениерегрессии:
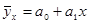 .
.
2. Система нормальных уравнений:

3. Определение параметров линейного уравнения регрессии:
Первый способ:
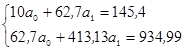
Поделим каждое уравнение на соответствующие коэффициенты при 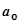 : первое уравнение – на 10, второе – на 62,7:
: первое уравнение – на 10, второе – на 62,7:

Вычтем из второго уравнения первое. Получим:
 ;
;
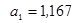 ;
; 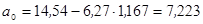 .
.
Второй способ:
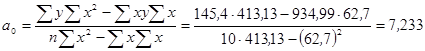 ;
;
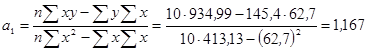 .
.
Линейное уравнение регрессии в числовом виде:
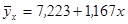 .
.
Коэффициент регрессии ( ) показывает, что при увеличении стоимости основных производственных фондов на 1 млн. руб. объем продукции в среднем будет увеличиваться на 1,167 млн. руб.
) показывает, что при увеличении стоимости основных производственных фондов на 1 млн. руб. объем продукции в среднем будет увеличиваться на 1,167 млн. руб.
Измерение тесноты связи
Для измерения тесноты связи при линейной зависимости используются: линейный коэффициент корреляции, коэффициент детерминации и коэффициент эластичности.
1. Линейный коэффициент корреляции. В 1889 г. Френсис Гальтон высказал мысль о коэффициенте, который мог бы измерить тесноту связи. В начале 90-х годов XІX в. К. Пирсон, Ф. Эджворт и Велдон получили формулу коэффициента корреляции.
Линейным коэффициентом корреляции называется среднее произведение отклонений вариантов взаимосвязанных признаков от их средних величин, разделенное на произведение их средних квадратических отклонений.
Первая формула:
 . (8.21)
. (8.21)
Вторая формула:
 , (8.22)
, (8.22)
где  ;
; 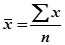 ;
; 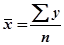 ;
;
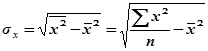 ;
; 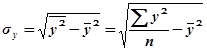 .
.
Вывод:
 ; (8.23)
; (8.23)
 ;
;
 . (8.24)
. (8.24)
Третья формула:
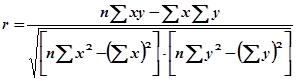 . (8.25)
. (8.25)
Четвертая формула.Коэффициент корреляции можно выразить через коэффициент регрессии:
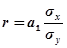 . (8.26)
. (8.26)
Вывод:
Решим в общем виде систему нормальных уравнений:
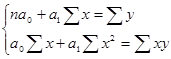 (8.27)
(8.27)
Поделим каждое уравнение на n:
 (8.28)
(8.28)
Поделим второе уравнение на  :
:
 (8.29)
(8.29)
Вычтем из второго уравнения первое:
 . (8.30)
. (8.30)
Определим параметр 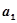 (коэффициент регрессии):
(коэффициент регрессии):
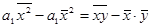 ; (8.31)
; (8.31)
 . (8.32)
. (8.32)
Выразим коэффициент корреляции r через коэффициент регрессии 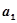 :
:
 . (8.33)
. (8.33)
Выведем дополнительные формулы для определения параметров уравнения регрессии. Для этого:
- выразим коэффициент регрессии 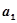 через коэффициент корреляции r:
через коэффициент корреляции r:
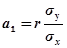 . (8.34)
. (8.34)
- из первого уравнения системы уравнений (8.29) найдем параметр 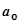 :
:
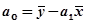 . (8.35)
. (8.35)
Параметры линейного уравнения регрессии можно определить по формулам:
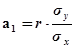 ; (8.36)
; (8.36)
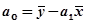 . (8.37)
. (8.37)
Линейный коэффициент корреляции изменяется в пределах:
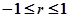 . (8.38)
. (8.38)
Знак «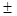 » при коэффициенте корреляции показывает направление связи («+» – прямая связь, «- » – обратная связь). Знак при коэффициенте корреляции совпадает со знаком при коэффициенте регрессии
» при коэффициенте корреляции показывает направление связи («+» – прямая связь, «- » – обратная связь). Знак при коэффициенте корреляции совпадает со знаком при коэффициенте регрессии 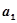 .
.
Если r = 0 – связь между признаками отсутствует;
r = 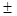 1 – связь между признаками функциональная;
1 – связь между признаками функциональная;
0 < | r | < 0,3 – связь слабая;
0,3 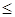 | r |
| r | 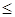 0,7 – связь средняя;
0,7 – связь средняя;
0,7 <| r |< 1 – связь тесная.
Линейный коэффициент корреляции дает качественную оценку тесноты связи. Для получения количественной оценки связи используются коэффициенты детерминации и эластичности.
2. Линейный коэффициент детерминации показывает, на сколько процентов вариация результативного признака обусловлена вариацией факторного признака:
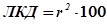 %. (8.39)
%. (8.39)
3. Коэффициент эластичности показывает, на сколько процентов в среднем изменится значение результативного признака при изменении факторного признака на 1%. Определяют средний и переменный коэффициенты эластичности:
средний:
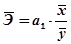 ; (8.40)
; (8.40)
переменный:
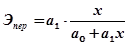 . (8.41)
. (8.41)
Пример 8.3. Определим линейный коэффициент корреляции, коэффициент детерминации и коэффициенты эластичности по данным таблицы 8.1.
1. Линейный коэффициент корреляции:
Первый метод:
 ,
,
где 1) 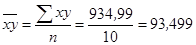 ;
;
2) 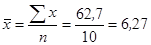 ;
;
3) 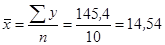 ;
;
4) 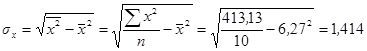 ;
;
5) 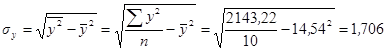 .
.
Второй метод:
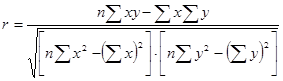 ;
;
 .
.
Третий метод:
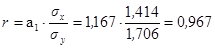 .
.
Линейный коэффициент корреляции показывает, что связь между стоимостью основных производственных фондов и объемом продукции тесная.
2. Коэффициент детерминации:
 %.
%.
Вариация объема продукции на 93,5% определяется вариацией стоимости основных производственных фондов.
3. Коэффициенты эластичности:
а) средний:
 .
.
При увеличении стоимости основных фондов на 1% объем продукции в среднем будет увеличиваться на 0,5%.
б) переменный (при заданном значении х). Допустим, что х = 5,2:
 .
.
При увеличении стоимости основных фондов от 5,2 млн. руб. до 5,252 млн. руб. (т.е. на 1%) объем продукции увеличится на 0,46%.
Рассмотренные показатели тесноты связи используется для ее оценки только при линейной форме связи.
Более универсальными показателями тесноты связи являются теоретическое корреляционное отношение (ТКО) и теоретический коэффициент детерминации (ТКД). Их можно использовать при любых формах связи, в том числе и при линейной.
1. Теоретическое корреляционное отношение (ТКО)представляет собой корень квадратный из отношения дисперсии теоретических значений результативного признака к дисперсии эмпирических значений результативного признака:
 , (8.42)
, (8.42)
где  - дисперсия эмпирических значений результативного признака;
- дисперсия эмпирических значений результативного признака;
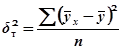 - дисперсия теоретических значений результативного признака.
- дисперсия теоретических значений результативного признака.
Теоретическое корреляционное отношение изменяется в пределах  .
.
Если 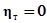 - связи нет,
- связи нет,
 - связь полная,
- связь полная,
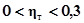 - связь слабая,
- связь слабая,
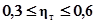 - связь средняя,
- связь средняя,
 - связь сильная (тесная).
- связь сильная (тесная).
2. Теоретический коэффициент детерминации (ТКД)показывает, на сколько процентов вариации результативного признака определяется вариацией факторного признака:
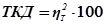 %. (8.43)
%. (8.43)
Пример 8.4. Рассчитаем теоретическое корреляционное отношение и теоретический коэффициент детерминации по данным таблиц 8.2 и 8.3.
1. Теоретическое корреляционное отношение (ТКО):
 .
.
Связь между урожайностью пшеницы и количеством вносимых удобрений тесная.
Таблица 8.3
Расчетная таблица для определения теоретического корреляционного