Перпендикуляр и наклонная
Наклонной, проведённой из данной точки к данной плоскости, называется любой отрезок, соединяющий данную точку с точкой плоскости, не являющийся перпендикуляром к плоскости.
Конец отрезка, лежащий в плоскости, называется основанием наклонной.
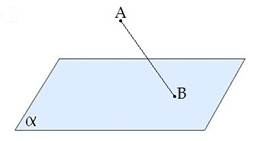
AB — наклонная;
B — основание наклонной.
Перпендикуляром, проведённым из данной точки к данной плоскости, называется отрезок, соединяющий данную точку с точкой плоскости, и лежащий на прямой, перпендикулярной плоскости.
Конец этого отрезка, лежащий в плоскости, называется основанием перпендикуляра.
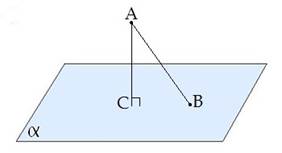
AC — перпендикуляр;
C — основание перпендикуляра.
Расстоянием от точки до плоскости называется длина перпендикуляра, проведённого из этой точки к плоскости.
Отрезок, соединяющий основания перпендикуляра и наклонной, проведённых из одной и той же точки, называется проекцией наклонной.
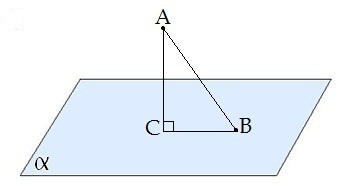
CB — проекция наклонной AB на плоскость α.
Треугольник ABC прямоугольный.
Углом между наклонной и плоскостью называется угол между этой наклонной и её проекцией на плоскость.
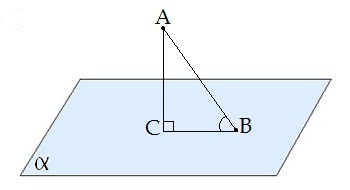
∢ CBA — угол между наклонной AB и плоскостью α.
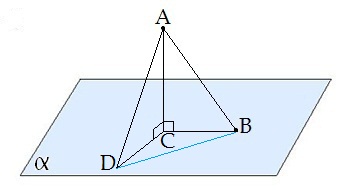
Если AD>AB, то DC>BC.
Если из данной точки к данной плоскости провести несколько наклонных, то большей наклонной соответствует большая проекция.
∢ DAB — угол между наклонными;
∢ DCB — угол между проекциями.
Отрезок DB — расстояние между основаниями наклонных.
Теорема о трех перпендикулярах
Теорема о трех перпендикулярах
Прямая, проведенная в плоскости через основание наклонной перпендикулярно к ее проекции на эту плоскость, перпендикулярна и к самой наклонной.
Дано:
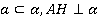
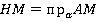
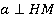
Доказать:
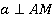
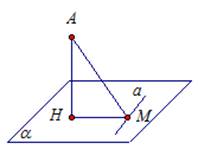
Рис. 4.
Доказательство:
Пусть нам дана плоскость α (рис. 4). Проведем перпендикуляр АН к плоскости α, АМ - наклонная, М – основание наклонной. НМ – это проекция наклонной АМ на плоскость α. В плоскости α проведем прямую а через основание наклонной М перпендикулярно проекции НМ. Нужно доказать, что прямая а перпендикулярна наклонной АМ.
Прямая АН перпендикулярна плоскости α, а значит, и всем прямым, лежащим в ней. Значит, прямая АН перпендикулярна прямой а. Прямая НМ перпендикулярна прямой а по условию. Имеем, что прямая а перпендикулярна двум пересекающимся прямым АН и НМ плоскости АНМ, значит, по признаку, прямая а перпендикулярна плоскости АНМ. Прямая АМ лежит в плоскости АНМ. Значит, прямая а перпендикулярна прямой АМ, что и требовалось доказать.
Обратная теорема
Прямая, проведенная в плоскости через основание наклонной перпендикулярно к ней, перпендикулярна и к ее проекции.
Дано:
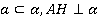
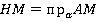
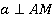
Доказать:
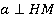
Доказательство:
Пусть нам дана плоскость α (рис. 4). Проведем перпендикуляр АН к плоскости α, АМ - наклонная. НМ – это проекция наклонной АМ на плоскость α. В плоскости α проведем прямую а через основание наклонной М перпендикулярно наклонной AМ. Нужно доказать, что прямая а перпендикулярна проекции HМ.
Прямая АН перпендикулярна плоскости α, а значит, и всем прямым, лежащим в ней. Значит, прямая АН перпендикулярна прямой а. Прямая AМ перпендикулярна прямой а по условию. Имеем, что прямая а перпендикулярна двум пересекающимся прямым АН и AМ плоскости АНМ, значит, по признаку, прямая а перпендикулярна плоскости АНМ. Прямая HМ лежит в плоскости АНМ. Значит, прямая а перпендикулярна прямой HМ, что и требовалось доказать.
Замечание к теореме о трех перпендикулярах
В доказанной прямой и обратной теореме точка М (основание наклонной) лежала на прямой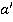 
, лежащей в плоскости α. Давайте проведем в плоскости α другую прямую а, которая параллельна 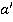. Тогда углы между прямыми a, АМ, НМ не изменятся. И из перпендикулярности прямой а и прямой АМ будет вытекать перпендикулярность прямой а и прямой НМ и наоборот.
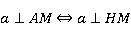
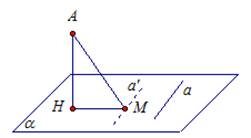
Рис. 5.
Задача 1
Из некоторой точки проведены к данной плоскости перпендикуляр и наклонная, угол между которыми равен 
.
а) Найти наклонную и ее проекцию на данную плоскость, если перпендикуляр равен d.
б) Найти перпендикуляр и проекцию наклонной, если наклонная равна m.
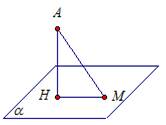
Рис. 6.
а) Дано:
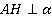
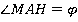
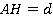
Найти:
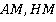
Решение:
Итак, имеем плоскость α, точку А, 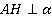(рис. 6). Вспомним, перпендикуляром называется отрезок АН, который проведен из точки А к плоскости 
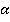, АМ – наклонная.
Мы имеем треугольник АНМ. Этот треугольник прямоугольный. Для того чтобы найти гипотенузу АМ, нужно катет АН разделить на косинус прилежащего угла НАМ.
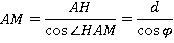
Найдем катет НМ.
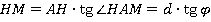
Ответ: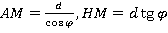 
б) Дано:
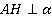
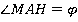
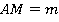
Найти:
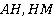
Решение:
АН перпендикуляр, АМ – наклонная, угол между ними , известна длина наклонной АМ. Нужно найти длину перпендикуляра АН и длину проекции НМ.
Задача снова свелась к решению прямоугольного треугольника НАМ. Найдем катет АН.
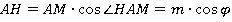
Найдем катет HМ.
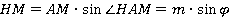
Ответ: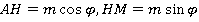 
Задача 2
Через вершину А прямоугольного треугольника АВС с прямым углом С проведена прямая АD, перпендикулярная к плоскости треугольника.
а) докажите, что треугольник СВD прямоугольный.
б) найдите ВD, если ВС = а, DС = b.
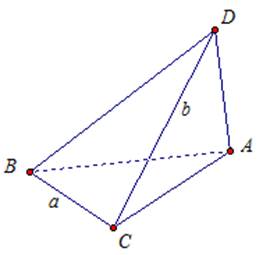
Рис. 7.
Дано: ∆АСВ = 90°, АD ⊥ АВС.
ВС = а, DС = b.
Доказать: ∆CBD – прямоугольный.
Найти: ВD
Решение:
а) Треугольник АВС прямоугольный, угол при вершине С прямой.
АD перпендикуляр к плоскости АВС. Требуется доказать, что треугольник СВD прямоугольный. Для наклонной DС отрезок АС является проекцией, потому что DA перпендикуляр ко всей плоскости АВС. По условию прямая ВС, лежащая в плоскости треугольника, перпендикулярна проекции наклонной АС, значит, по теореме о трёх перпендикулярах она перпендикулярна и самой наклонной CD. То есть ВС ⊥ CD, а значит ∆ВСD прямоугольный.
б) Найдем гипотенузу ВD из прямоугольного треугольника СВD с помощью теоремы Пифагора.
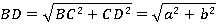
Ответ: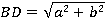 
Задача 3
Отрезок SО - перпендикуляр к плоскости квадрата АВСD, где точка О – центр квадрата.
Доказать: ВD ⊥ SC
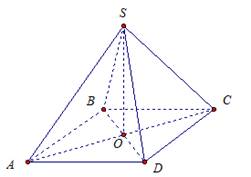
Рис. 8.
Доказательство:
Первый способ.
Имеем квадрат, центр квадрата точка О, SО - перпендикуляр. Значит, для наклонной SC отрезок ОС есть проекция.
Прямая ВD перпендикулярна прямой ОС, которая является проекцией наклонной SC, значит, по теореме о трех перпендикулярах, прямая ВD перпендикулярна наклонной SC.
Второй способ.
Прямая SО перпендикулярна плоскости АВС, а значит, и прямой ВD, лежащей в ней.
Прямая ВD перпендикулярна SО и прямая ВD перпендикулярна прямой АС по свойству квадрата.
Получаем, что прямая ВD перпендикулярна двум пересекающимся прямым плоскости SОС, значит, она перпендикулярна ко всей плоскости SОС, а значит, и к прямой SC, лежащей в этой плоскости.