ЛАБОРАТОРНАЯ РАБОТА
По дисциплине: «Математические модели в естествознании и экологии»
Выполнила
студентка группы А-13-09
каф. Прикладной Математики
Шорникова Дарья
Преподаватель
Ижуткин В.С.
Москва, 2013
МОДЕЛЬ ДВУХВОЗРАСТНЫХ ПОПУЛЯЦИЙ МИКРООРГАНИЗМОВ
Однородность клеток в микробной популяции всегда относительна. Большую роль в процессах роста микробной популяции играет возрастная структура. Делиться, т.е. увеличивать численность популяции, способны только клетки, достигшие определенного возраста (или определенного размера). Возрастная гетерогенность популяции может служить причиной сложной немонотонной динамики ее численности.
Рассмотрим простейшую двухвозрастную модель клеточной популяции (Степанова, 1985). Популяция разбита на две группы клеток: молодые и старые.
Будем считать, что клетки первой группы интенсивно растут, но не достигли физиологической зрелости и неспособны делиться. Члены второй группы способны к делению. Процесс деления может быть задержан при помощи различных ингибиторов. Уравнения для численностей молодых (N1) и старых (N2) клеток имеют вид:
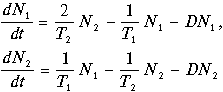
Здесь Т1 - среднее время созревания молодой клетки, Т2 - среднее время пребывания старой клетки в репродуктивном периоде, D ‑ скорость протока (вымывания клеток из культиватора). Множитель 2 в первом уравнении отражает тот факт, что старая клетка делится на две молодые.
Данная система дифференциальны уравнений решается численно с помощью неявного метода Эйлера.
Программное средство позволяет работать с двумя интерпретациями данной модели. Первая интерпретация представляет двухвозрастную модель культуры микроорганизмов в культиваторе. Вторая интерпретация представляет возрастной состав кафедры учебного заведения.
|
|
На кафедре учебного заведения преподают опытные сотрудники, которые за время T1 обучают каждый двух молодых сотруднико и сами могут преподавать в течение времени T2. В качестве параметра D используется коэффициент "мотивации" сотрудников, подкрепленный деньгами. Желаемая заработная плата для начинающего молодого сотрудника - 30 тыс. руб, для опытного - 50 тыс. руб. Изменение уровня оплаты труда влияет на численность сотрудников. Данная модель позволяет моделировать возрастной состав кадров на кафедре учебного заведения с учетом этих факторов.
Интерфейс работы программы
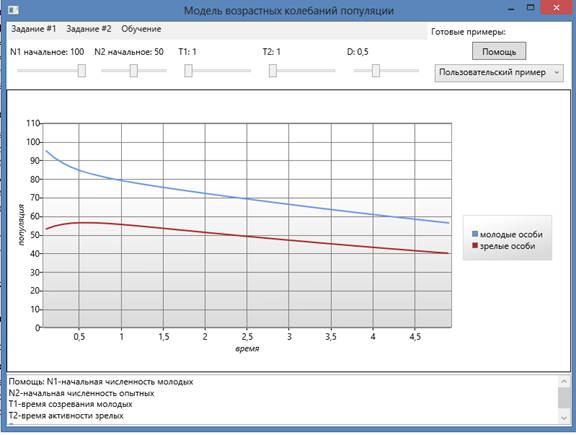
Окно с информацией о модели

Демонстрационный пример
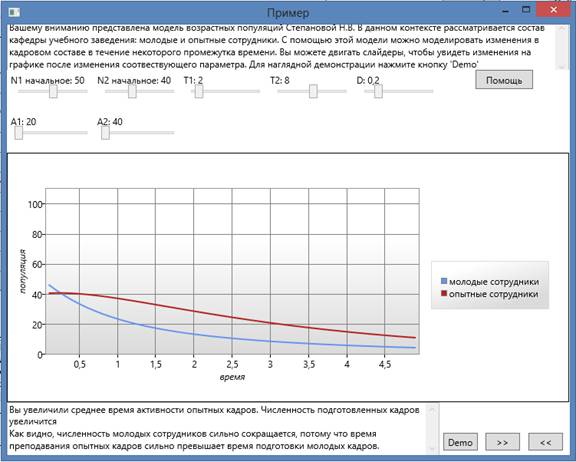
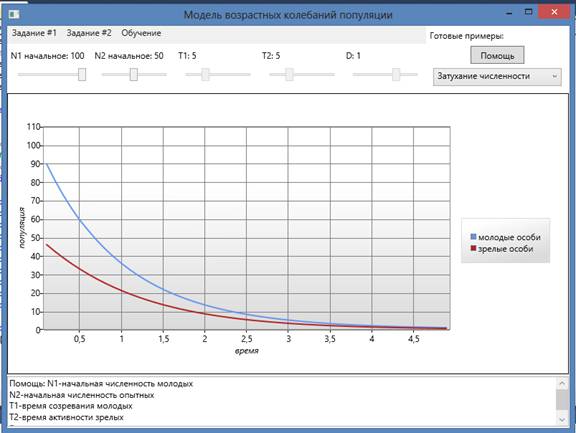
Пример: численность микроорганизмов убывает со временем
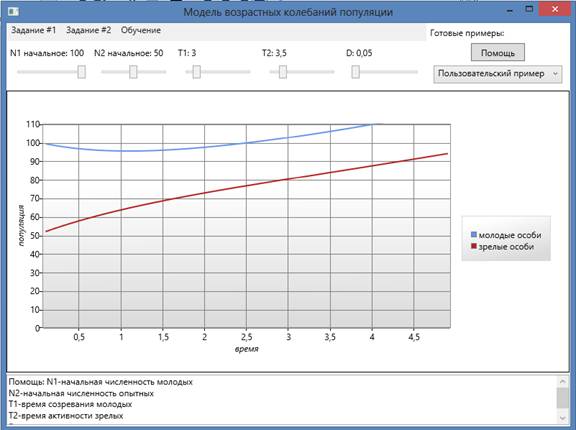
Пример: численность микроорганизмов возрастает со временем
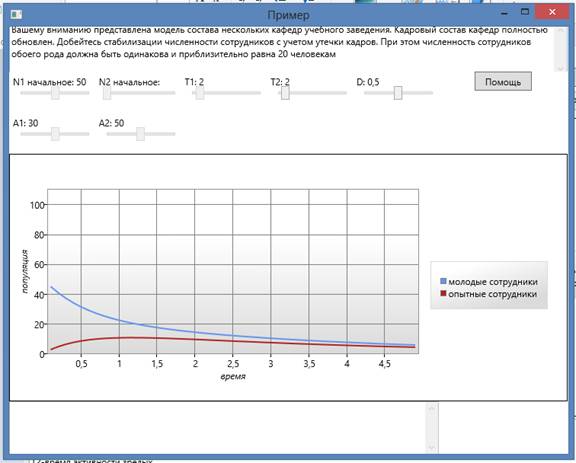
Упражнение
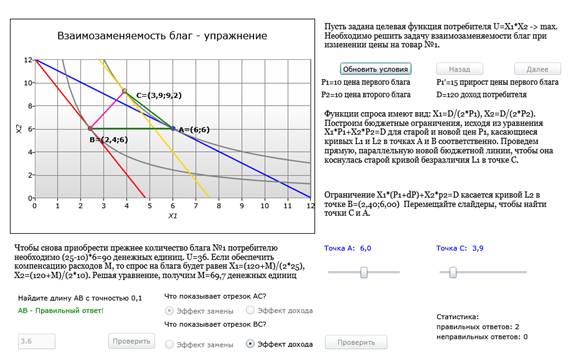
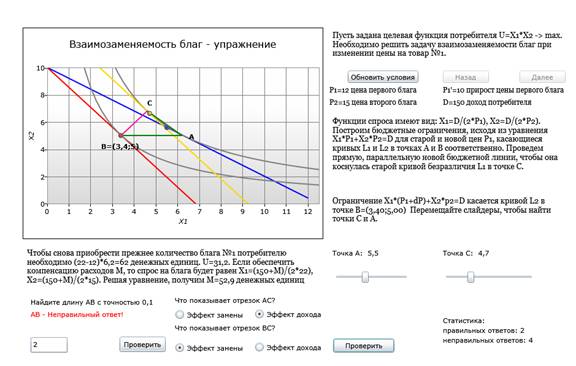
ВЗАИМОЗАМЕНЯЕМОСТЬ БЛАГ. ЭФФЕКТ КОМПЕНСАЦИИ
Решение задачи потребительского выбора сводится к максимизации значения функции U, зависящей от спроса на блага A и B, которая наилучшим образом решает потребности потребителя при заданном бюджетном ограничении. При изменении цен на товары A и B меняется и спрос на них. Как должен измениться уровень дохода потребителя, чтобы по-прежнему удовлетворить его потребности?
Задача является симметричной относительно изменения цен, поэтому можно рассматривать только изменение цены на товар A. При увеличении цены на товар A при неизменном уровне дохода потребитель будет покупать больше товара B - это эффект замены. При увеличении дохода потребителя он может позволить себе купить больше товара A, не отказывая себе в покупке других товаров - это эффект дохода. В терминах экономики эффект дохода - переход с одной кривой безразличия на другую, а эффект замены - движение по одной кривой безразличия. Кривая безразличия - это геометрическая интерпретация равнозначного для потребителя выбора.
|
|
Функции спроса на товары имеют вид: Xi = D/(2*Pi), где D - доход потребителя, а Pi - цена товара i. Модель позволяет поэтапно проследить изменение предпочтений потребителя при изменении цен и компенсации потребителю его дохода.
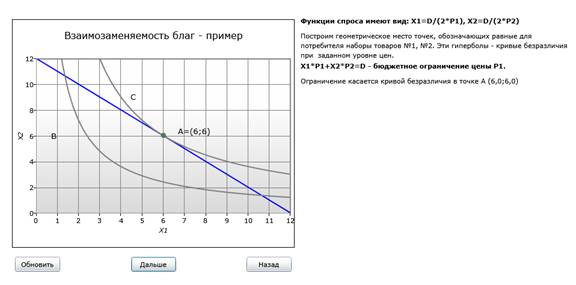
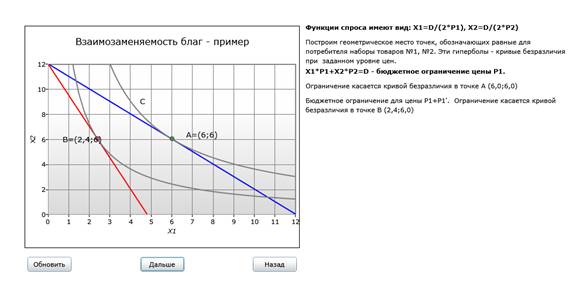
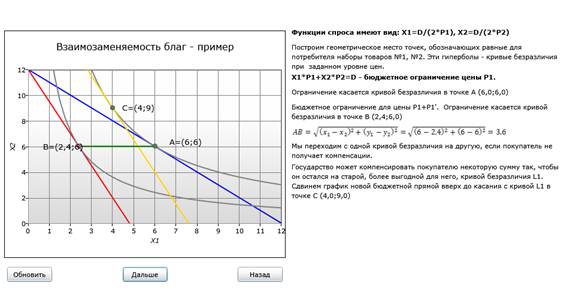
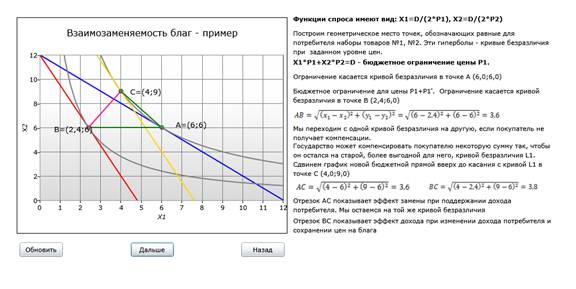
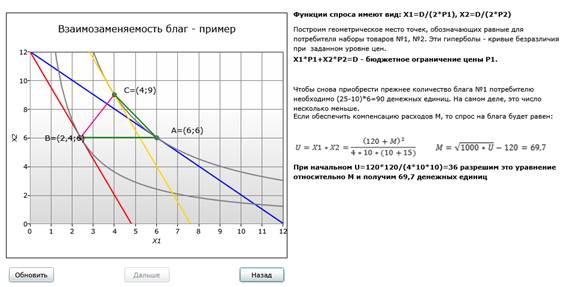
В примере пользователю предлагается рассчитать длину отрезка AB после нахождения точек пересечения кривых безразличия и линий бюджентного огранчения. Правильно найденные точки выделяются на графике жирным и получают отображение координат. Также пользователю предлагается определить, какие отрезки обозначают эффект дохода и замены.
Ведется статистика ответов пользователя.