Получим некоторые вспомогательные утверждения и оценки связанные с оператором L.
Утверждение 1.2.1. Пусть выполнено условие: i) k(y)≥0 - кусочно-непрерывная функция на [0,1] и к(0)=0. Тогда оператор L положительно определён и существенно самосопряжен в 
.
Утверждение 1.2.2. Пусть выполнено условие: i) k(y)≥0 - кусочно-непрерывная функция на [0,1] и к(0)=0. Тогда спектр оператора L дискретен.
Для доказательства этих утверждений сперва докажем следующие леммы.
Лемма 1.2.1 Пусть выполнено условие i). Тогда для любого 
справедлива оценка
где с>0- постоянное число, не зависящее от u(x,y).
Доказательство. Для 
имеем:
;
Отсюда на основании условия i) и неравенства Коши-Буняковского имеем:
Лемма 1.2.1 доказана. Здесь учитывалось вещественность коэффициентов оператора L.
Лемма 1.2.2. Пусть выполнено условие i). Тогда L симметричный оператор, т.е.
.
Доказательство. Для 
имеем:
(1.2.5)
Интегрируя по частям, учитывая граничные условия (1.2.2) и пользуясь тем, что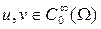 
находим:
Отсюда получим:
.
Точно также интегрируя по частям и учитывая граничные условия (1.2.3) получим:
.
.
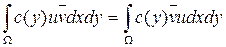Отсюда и из (1.2.5) следует, что
.
В силу непрерывности скалярного произведения равенство 
справедливо для всех 
. Следовательно, L симметричный оператор.
Лемма 1.2.2 доказана.
Лемма 1.2.3 Пусть выполнено условие i). Тогда L положительно определенный оператор.
Доказательство. Составим квадратичную форму:
.
Интегрируя по частям и принимая во внимание граничные условия (1.2.2), (1.2.3) найдем:
Точно также:
Тогда получим:
.
Лемма 1.2.3 доказана.
Рассмотрим оператор
определенный первоначально на 
, оператор допускает замыкание. - множество бесконечно дифференцируемых функций удовлетворяющих условию 
.
Лемма 1.2.4 Пусть выполнено условие i). Тогда:
а) для всех 
справедлива оценка 
;
б) оператор 
существенно самосопряжен.
Доказательство. Для всех 
имеем:
,
,
.
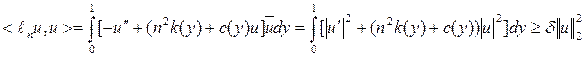Отсюда, используя неравенства Коши-Буняковского, получаем, что последнее неравенство, в силу непрерывности нормы, справедливо
для всех 
.
Нетрудно проверить, что оператор – симметрический. Действительно, интегрируя по частям имеем:
.
Это неравенство в силу непрерывности скалярного произведения верно для всех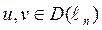 
. Лемма 1.2.4 будет доказана, если мы докажем что 
D(
) плотно в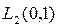 
Докажем, это от противного, что множество значений не является плотным в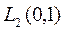 
. Тогда существует элемент 
такой, что 
, т.е. 
для всех 
. Тогда по теореме Рисса имеет место равенство
,
где 
. Отсюда, в силу плотности D() в 
, следует, что
.
Далее, непосредственно можно убедится, что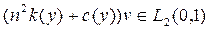 
отсюда 
.
Теперь, если показать, что v=0, то придем к противоречию и лемма будет доказана. Для этого рассмотрим следующее выражение:
.
Верны следующие, выкладки:
(1.2.6)
По предположению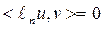 
. Тогда из равенства (1.2.6) следует 
или
(1.2.7)
Предположим, что 
Так как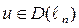 
, т.е. мы можем брать произвольно функцию u.
Пусть 
.
Тогда
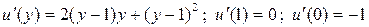(1.2.8)
Подставляя (1.2.8) в (1.2.7) находим 
. Точно также докажем, что 
. Таким образом 
и для этой функции справедливо неравенство
.
Полученное неравенство показывает, что, в силу 
.
Лемма 1.2.4 доказана полностью.