Из леммы 1.2.4 следует, что 
положительно определенный и самосопряженный оператор. Далее, пользуясь леммой Реллиха получаем, что спектр оператора 
дискретен в том и только в том случае если множество
(1.2.13)
компактно в 
. Рассмотрим множество
.
Непосредственно можно проверить, что 
. Так как множество 
компактно в , то отсюда сразу следует, что 
также компактно в 
.
Далее, пользуясь методом разделения переменных получаем, что, если l точка спектра оператора L, то l является точкой спектра одного из операторов
И наоборот, если l- точка спектра одного из операторов 
, то l является точкой спектра оператора L. Теперь доказываемое утверждение следует из леммы Реллиха и леммы 1.2.4.
При доказательстве лемм 1.2.5 и 1.2.6 мы будем пользоваться рассуждениями и выкладками работы [19].
Лемма 1.2.5. Пусть выполнены условия i)-ii). Тогда для 
справедлива оценка
(1.2.14)
Доказательство. Поступим следующим образом. Пусть 
и рассмотрим функционал
(1.2.15)
Обозначим через 
интеграл 
, а через 
интеграл 
, т.е.
, 
.
Вычислим интеграл :
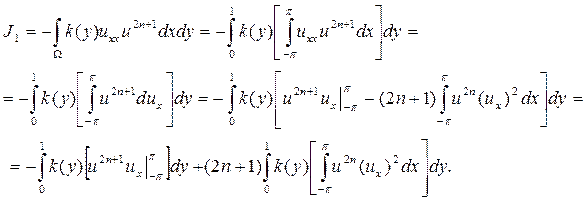
Отсюда, в силу (1.2.2), имеем:
, (1.2.16)
где
Теперь рассмотрим интеграл 
:
Учитывая условия (1.2.3) находим:
(1.2.17)
Подставляя (1.2.16) и (1.2.17) в (1.2.15), имеем:
.
Здесь, учитывая тот факт, что первые два интеграла неотрицательны, получаем
. (1.2.18)
Из (1.2.18) используя неравенство Гёльдера имеем:
при 
.
Отсюда и из неравенства (1.2.18) имеем:
,
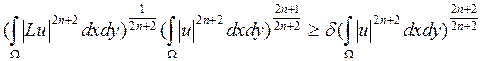или
.
Отсюда следует неравенство (1.2.14), т.е.
В силу непрерывности нормы 
неравенство (1.2.14) верно и для 
.
Лемма 1.2.5 доказана.
Лемма 1.2.6. Пусть выполнены условия i)-ii). Тогда:
а) для 
справедлива оценка
; (1.2.19)
б) существует непрерывный обратный оператор в 
.
Доказательство. Для дюбого 
рассмотрим функционал:
(1.2.20)
где 
. Обозначим через J1 интеграл 
, через J2 интеграл 
, т.е.
, 
.
Вычислим интеграл J1:
В последнем равенстве первый интеграл равен нулю.
Действительно:
Далее, учитывая это получаем, что
(1.2.21)
Далее, вычислим интеграл J2:
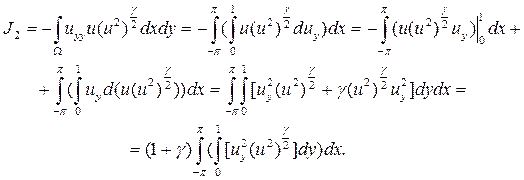(1.2.22)
Здесь вне интегральный член равен нулю в силу (1.2.3).
Итак, пользуясь (1.2.21) и (1.2.22), из (1.2.20) имеем:
.
Отсюда
.
Учитывая, что 
, получим:
.
Применяя последнему неравенству неравенство Гельдера, находим:
или
. (1.2.23)
Выберем 
следующим образом:
.
В результате получим оценку
или
.
Отсюда
Последнее неравенство в силу непрерывности нормы справедливо для любого 
.
Неравенство (1.2.20) доказано.
Из общей теории сопряженных операторов имеем:
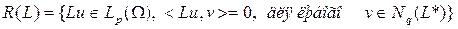(1.2.24)
где 
.
Известно, в случае ограниченной области, что
.
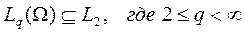Следовательно, 
Отсюда, если 
.
Так как, в силу утверждения, оператор L в 
положительно определен и самосопряжен, поэтому 
. Отсюда и из (1.2.24) следует, что
. (1.2.25)
Из неравенства (1.2.19) и из равенства (1.2.25) следует, что существует непрерывный обратный оператор 
. Лемма 1.2.6 доказана.
Лемма 1.2.7. Пусть выполнены условия i)-ii) и пусть 
. Тогда справедливо равенство
,
где 
.
Доказательство. Известно, 
и в силу леммы 1.2.6 существует 
и 
. Из общей теории линейных операторов следует, что существует ограниченный линейный оператор 
и справедливо равенство
, (1.2.26)
при 
.
,
это означает, что
и 
. (1.2.27)
Мы здесь воспользовались, тем, что D(L) плотно в 
.
С другой стороны, при 
.
Здесь 
плотно в 
, поэтому
. (1.2.28)
Равенства (1.2.27) и (1.2.28) показывают, что оператор 
является обратным к 
, т.е. 
. Отсюда и из (1.2.26) следует, что
.
Полагая 
, получим
. (1.2.29)
Обозначим через 
, замыкание оператора
,
в пространстве 
.
Лемма 1.2.8. Пусть выполнены условия i)-ii). Тогда для любого 
справедлива оценка
(1.2.30)
и оператор 
непрерывно обратим.
Доказательство. Для удобства рассмотрим случай q=4, т.е. 
. Согласно (1.2.14), для произвольных 
имеет место оценка
. (1.2.31)
Из леммы 1.2.7 следует, что существует сопряженный 
, который непрерывно обратим в 
(
- сопряженный оператор к оператору L определенного в 
).
Нетрудно установить, что 
. Поэтому, если докажем, что 
, то 
.
Последнее равенство доказывает лемму 1.2.8 в случае q=4.
Известно, что 
. Согласно леммам 1.2.2-1.2.4, оператор 
положительно определен и существенно самосопряжен в пространстве 
. Поэтому для 
плотно в . Пусть 
. Поскольку множество плотно в 
, существует последовательность элементов 
. С другой стороны, в силу (1.2.31), из неравенства
следует 
.
Ясно, что 
, покажем h=v. Для этого рассмотрим функционал
Поскольку, в силу леммы 1.2.6, 
плотно, отсюда следует v=h. Это означает 
. Таким образом, доказано равенство 
. Случай q=4 доказан. Теперь доказываемая лемма следует из леммы 1.2.7 и интерполяционной теоремы Рисса-Торина [44].
Доказательство теоремы 1.2.1, 1.2.2. Теоремы 1.2.1, 1.2.2 непосредственно следует из лемм 1.2.6 и 1.2.8.