Случайная величина
2.2.1 Основные определения.
Случайная величина – это числовая функция на пространстве элементарных исходов (ПЭИ) Ω. Обозначают случайные величины буквами X, Y, Z и т.п. Запись X = X (w) означает, что случайная величина X является функцией элементарных исходов ω. Величина X может принять некоторое числовое значения xi, определяемое наблюдавшимся элементарным исходом w j, который обладает признаком-значением xi. Совокупность всех возможных значений xi случайной величины X называется её спектром.
В зависимости от природы моделируемого явления случайная величина может иметь непрерывный, дискретный или смешанный спектр.
Содержательно случайная величина X эквивалентна пространству Ω, т.е. она представляет собой достоверное событие, а её возможные значения xi – несовместные в совокупности и, как следствие, несовместные попарно события, т.е. xi ∩ xj = Ø. При этом, естественно, что для дискретной случайной величины объединение всех элементов спектра вырождается в логическую сумму и образует полную группу событий:
 = x 1 + x 2 + … + xi + … + xn = Ω. (37)
= x 1 + x 2 + … + xi + … + xn = Ω. (37)
На основании Аксиом 3 и 2 получаем:
 =
=  = P (Ω) = 1. (38)
= P (Ω) = 1. (38)
Задача 2.10. Построить случайную величину, являющуюся «количеством выпадений герба » при трёх подбрасываниях симметричной монеты.
Решение. Сначала построим ПЭИ Ω, моделирующее эксперимент. Подбрасывание монеты – это комбинации с возвращениями (2.1.3), общее число которых r определяется как nm (9), где n = 2 – число сторон монеты, а m = 3 – количество подбрасываний.
ПЭИ Ω состоит из r = 23 = 8-и элементарных исходов:
w1 = { ццц }; w2 = { ццг }; w3 = { цгц }; w4 = { гцц };
w5 = { ггц }; w6 = { гцг }; w7 = { цгг }; w8 = { ггг }.
Здесь «ц » и «г » – примитивы, реализующиеся при однократном подбрасывании монеты. Все элементарные исходы ω j являются логическими произведениями стохастически не связанных примитивов и обладают равными вероятностями:
P(ω j) = 1 / 8. (39)
Введём интересующую нас случайную величину X = {количество выпадений герба при трёхкратном подбрасывании монеты}. Перечислим её возможные значения (элементы спектра):
X ={ x 0 = 0; x 1 = 1; x 2 = 2; x 3 = 3} = X (w).
Раскроем структуру каждого элемента спектра xi = xi (w j) этой случайной величины:
x 0 = {w1}; x 1 = {w2, w3, w4}; x 2 = {w5, w6, w7}; x 3 = {w8}.
По Аксиоме 3, учтя вероятности элементарных исходов (39), вычислим вероятности этих виртуальных событий и найдём их сумму, которая, в соответствие с (38), должна равняться единице:
P(X = x0) = p0 =  = 1 / 8;
= 1 / 8;
P(X = x1) = p1 =  = 3 / 8;
= 3 / 8;
P(X = x2) = p2 =  = 3 / 8;
= 3 / 8;
P(X = x3) = p3 =  = 1 / 8;
= 1 / 8;
 = 1/8 + 3/8 + 3/8 +1/8 = 1. #
= 1/8 + 3/8 + 3/8 +1/8 = 1. #
Элементы спектра xi или непрерывно заполняют какой-либо отрезок, интервал числовой оси, или представляют собой отдельные точки, или являются объединениями таких множеств. Описание случайной величины (СВ) может иметь разную форму:
X = {словесное определение} – непрерывная или дискретная СВ;
X = { x 1, x 2,…, xi,…, xn } – дискретная СВ;
X = { 
 } – CВ, непрерывная на отрезке
} – CВ, непрерывная на отрезке 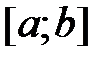 ;
;
X = {  ]– ∞; + ∞[} – СВ, непрерывная на всей числовой оси.
]– ∞; + ∞[} – СВ, непрерывная на всей числовой оси.
Возможные значения xi случайной величины X, будучи событиями, характеризуются соответствующими вероятностями P (X = xi) = pi для дискретного случая, либо  = p для непрерывного. Для дискретной случайной величины вероятности могут быть найдены одним из способов, указанных в разделе 2.1. Вопрос о вероятностях событий, природа которых непрерывна, будет конкретизирован в следующих разделах.
= p для непрерывного. Для дискретной случайной величины вероятности могут быть найдены одним из способов, указанных в разделе 2.1. Вопрос о вероятностях событий, природа которых непрерывна, будет конкретизирован в следующих разделах.
Зависимость между элементами спектра случайной величины и соответствующими вероятностями называется «законом распределения вероятностей случайной величины », «законом распределения », просто «законом » или «распределением ». Закон может иметь аналитическую, табличную или графическуюформу. При этом, формы законов распределения дискретных и непрерывных случайных величин имеют свои особенности.
Распределение дискретной случайной величины.
В зависимости от условий, аналитическая форма распределения дискретной случайной величины задаётся одним из способов, описанных в разделе 2.1:
Mi / N – классическая формула,
P (X = xi)= pi =  – следствие третьей аксиомы, (40)
– следствие третьей аксиомы, (40)
Pn (m = xi) – формула Бернулли.
Здесь Mi – количество равновозможных исходов из общего их числа N, благоприятствующих xi, а w j – это те элементарные события, которые имеют числовое значение xi.
Табличная форма дискретного закона называется «рядом распределения дискретной случайной величины »:
| X = xi | x 1 | x 2 | … | xn |
| P (X = xi) = pi | p 1 | p 2 | … | pn |
(41)
Вероятности pi вычисляются по одной из формул (40), а сумма, согласно (38), должна равняться единице, т.е. Σ pi = 1.
Графическая форма закона – это график, построенный по формулам (40) или по ряду (41) (см. Рис.2.8). Он называется «многоугольником » или «полигоном » распределения.
p
pi -
-
… -
p 1 -
0 x 1 x 2 x 3 xi xn -1 xn X
Рис. 2.8 Многоугольник распределения.
Точки графика соединяются между собой отрезками прямых только для наглядности. Проводить по графику обратную интерполяцию нельзя, так как промежуточные точки не принадлежат спектру случайной величины, т.е. являются невозможными событиями с нулевой вероятностью.
Функция распределения.
2.2.3.1 Определение и свойства.
Функция распределения (ФР) – это универсальная аналитическая форма закона распределения, используемая для описания как дискретных, так и непрерывных случайных величин. По определению, функция распределения представляет собой вероятность того, что случайная величина X меньше некоторого фиксированного значения x:
F (x)= P (X < x). (42)
Очевидно, что, будучи вероятностью, F (x)  [0;1]. Рассмотрим подробнее поведение ФР дискретной случайной величины. Значение этой функции в точке «x » равно сумме вероятностей pi по всем xi < x, т.е.:
[0;1]. Рассмотрим подробнее поведение ФР дискретной случайной величины. Значение этой функции в точке «x » равно сумме вероятностей pi по всем xi < x, т.е.:
F (x) =  . (43)
. (43)
Результаты вычислений по формуле (43) заносят в расширенный для этого ряд распределения:
| X = xi | x 1 | x 2 | x 3 | … | xn | - |
| P(X = xi) = pi | p 1 | p 2 | p 3 | … | pn | - |
| P(X<x)=F(x) | p 1 | p 1 + p 2 | … | p 1 +…+ pn- 1 |
(44)
Определение (42) и его реализация (43) для дискретной случайной величины позволяют обосновать следующие свойства функции распределения:
1) F (x 2)  F (x 1), если x 2> x 1, т.е. ФР – неубывающая функция;
F (x 1), если x 2> x 1, т.е. ФР – неубывающая функция;
2) F (x) = 0, когда x < x 1. Более широко, F (–∞) = 0.
3) F (x) = 1, когда x > xn. Неограниченный рост аргумента не увеличивает значение ФР: F (∞) =1.
График функции распределения дискретной случайной величины (СВ) отображается ступенчатой функцией (рис. 2.9).
F (x)
1.0 - ----------------------------------------
- pi
p 1+ p 2 -
-
p 1 -
0 x 1 x 2 … xi … xn -1 xn X
Рис. 2.9 Функция распределения дискретной СВ.
Задача 2.11. По данным Задачи 2.10 получить все формы закона распределения.
Решение. Все необходимые вычисления, предписанные аналитическими формами закона (40) и (43), уже выполнены в Задаче 2.10. Остаётся свести результаты в расширенный ряд (44):
Полигон распределения и график ФР представлены ниже на рисунках 2.10 и 2.11.
| X = xi | x 0=0 | x 1=1 | x 2=2 | x 3=3 | |
| P (X = xi) = pi | p 0=1/8 | p 1=3/8 | p 2=3/8 | p 3=1/8 | |
| P (X < x)= F (x) | 1/8 | 4/8 | 7/8 |
Для случайной величины непрерывного типа функция распределения будет обладать теми же свойствами, которые были обоснованы для дискретной случайной величины. При этом, непрерывная случайная величина может существовать как на конечном отрезке [ a; b ], так и на всей числовой оси ]– ∞; + ∞[:
1) F (x 2)  F (x 1), если x 2 > x 1;
F (x 1), если x 2 > x 1;
2) F (x) = 0, когда x < a. Более широко, F (– ∞) = 0.
3) F (x) = 1, когда x  b. Аналогично, F (∞) = 1.
b. Аналогично, F (∞) = 1.
p F (x)
1 -
3/8 - 7/8 -
4/8 -
1/8 - 1/8 -
0 X | | | X
x 0=0 x 1=1 x 2=2 x 3=3 x 0=0 x 1=1 x 2=2 x 3=3
Рис. 2.10 Полигон. Рис. 2.11 Функция распределения. #
График функции распределения для непрерывной случайной величины, когда X  ]– ∞; + ∞[, представлен на следующем рисунке (Рис. 2.12). Если же непрерывная случайная величина существует только на отрезке [ a; b ], то ее левая ветвь сливается с осью абсцисс от точки «a » влево, а правая совпадает с линией y = 1 от точки b вправо (Рис. 2. 13).
]– ∞; + ∞[, представлен на следующем рисунке (Рис. 2.12). Если же непрерывная случайная величина существует только на отрезке [ a; b ], то ее левая ветвь сливается с осью абсцисс от точки «a » влево, а правая совпадает с линией y = 1 от точки b вправо (Рис. 2. 13).
|
|
Рис. 2.12 X  ]– ∞; + ∞[. Рис. 2.13 X
]– ∞; + ∞[. Рис. 2.13 X  [ a, b ].
[ a, b ].
2.2.3.2 Вероятность попадания СВ на полуинтервал.
Рассмотрим задачу об определении вероятности попадания случайной величины на полуинтервал [ a; b). Решение этой задачи легко выполняется с использованием универсальной формы закона распределения – функции распределения.
Дано: X – случайная величина, для которой известно выражение ее функции распределения F (x) = P (X < x) и полуинтервал с известными границами [ a; b).
Найти: Вероятность попадания случайной величины X на полуинтервал [ a; b), т.е. P (X  [ a; b)) = P (a ≤ X < b) –?
[ a; b)) = P (a ≤ X < b) –?
Решение: Введем следующие события: A = { X < a }, B = { X < b } и C = { a ≤ X < b }. Два из них, A и C, несовместны, т.е. AC = Ø, а событие B представляет собой их логическую сумму: B = A + C. Вероятность суммы B равна, согласно Аксиоме 3, сумме вероятностей её слагаемых A и C. Интересующая нас вероятность события C может быть найдена как разность вероятностей событий B и A: P (C) = P (B) – P (A). Заменив в этом соотношении события A, B и C введенными выше неравенствами, получим:
P(a ≤ X < b) = P(X < b) – P(X < a).
Однако, вероятности в правой части – это значения функции распределения в точках b и a, соответственно. Окончательно получаем:
P(a ≤ X<b) = 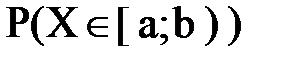 = F(b) – F(a). (45)
= F(b) – F(a). (45)
Итак, вероятность попадания случайной величины на полуинтервал численно равна приращению её функции распределения на этом полуинтервале.
На рисунке (Рис.2.14) дана геометрическая интерпретация полученного результата на примере непрерывной случайной величины.
| F (x) |
| 1.0 |
| X |
| a |
| b |
| F (a) |
| F (b) |
| P (a ≤ X < b)= F (b) - F (a) |
Рис. 2.14 Вероятность попадания СВ на полуинтервал.
Для дискретной случайной величины формула (45) с учетом определения (43) может быть преобразована к виду
P (a ≤ X < b)=  –
–  =
=  . (46)
. (46)
Практически, при больших по объему спектрах дискретных случайных величин, пользование формулой (46) становится затруднительным. Выход из этой ситуации найден давно и заключается в аппроксимации дискретного распределения непрерывным. Конкретные решения проблемы будут продемонстрированы позже при изучении наиболее распространенных законов распределения.
Если границы полуинтервала [ a; b) сближаются неограниченно, то, в пределе, для непрерывной случайной величины
P (a → b ≤ X < b) = F (b) – F (b) = P (X = b) ≡ 0,
т.е. вероятность попадания непрерывной случайной величины в точку равна нулю, хотя такое событие и не является невозможным.
В связи с последним, при решении задачи об определении вероятности попадания непрерывной случайной величины на полуинтервал мы будем заменять его интервалом, так как численно вероятности этих событий равны.
2.2.4 Плотность распределения непрерывной СВ.
Кроме функции распределения (ФР) для характеристики непрерывной случайной величины удобно ввести еще одну аналитическую форму закона распределения, называемую плотностью распределения (ПР).
Вероятность попадания непрерывной случайной величины на интервал длиной Δ x определяется с помощью её ФР (45):
P (x < X < x + ∆ x) = F (x + Δ x) – F (x).
Отнесем эту вероятность к длине интервала, устремив последнюю к нулю:

 =
= 
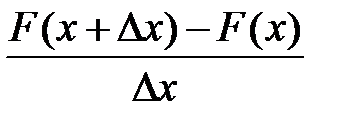 = F ʹ(x) = f (x). (47)
= F ʹ(x) = f (x). (47)
Если предел (47) существует, то данное выражение представляет собой классическое определение производной непрерывной функции F (x), которая и называется плотностью распределения f (x).
Дифференциал ФР dF (x) и равное ему произведение f (x) dx называют элементом вероятности непрерывной СВ. От дифференциального уравнения элемента вероятности
dF (x) = f (x) dx (48)
по правилам интегрального исчисления переходим к выражению для нахождения вероятности попадания непрерывной СВ на конечный интервал (x 1 = a; x 2 = b):
P (a < X < b) = F (b) – F (b) =  =
=  . (49)
. (49)
Если в выражении (49) a = – ∞, а b = x, то
P (– ∞ < X < x) = P (X < x) = F (x) =  . (50)
. (50)
Выражение (50) отражает обратную связь между плотностью и функцией распределения. Форма этой связи позволила дать для ФР и ПР дополнительные названия: интегральный – F (x) и дифференциальный – f (x) законы распределения вероятностей.
Определение ПР как производной от ФР и соотношение (50) позволяют сформулировать такие свойства плотности:
1) f (x) ≥ 0,так как F (x) – неубывающая функция;
2) f (– ∞) = f (∞) = 0, так как F ´(0) = F ´(1) = 0;
3)  =1, что следует из (50), когда верхний предел x → ∞.
=1, что следует из (50), когда верхний предел x → ∞.
Последнее свойство называется основным свойством ПР.
На рисунке (Рис.2.15) представлены иллюстрации, разъясняющие геометрический смысл свойств ПР и соотношений (48) и (50).
| X |
| f (x) |
| a |
| b |
| f (x) dx |
| xx + d x |
P (a < X < b) = 
|
Рис. 2.15 Плотность распределения.
2.2.5 Моменты и числовые характеристики СВ.
Закон распределения случайной величины содержит полную информацию о ней и позволяет вычислять вероятности любых событий, связанных с этой величиной. Задача установления закона распределения требует значительных усилий от исследователя. Практически, для многих целей бывает достаточно знать лишь какую-то узкую область, в которой существует б о льшая часть спектра случайной величины. Кроме того, можно количественно охарактеризовать как центр такой области, так и силу разброса случайной величины, асимметричность спектра относительно центра и некоторые другие показатели, которые называются числовыми характеристиками СВ.
2.2.5.1 Характеристики положения СВ на числовой оси.
Чаще всего в качестве характеристики положения случайной величины используется математическое ожидание, имеющее целый ряд синонимов: центр тяжести, центр рассеивания, центр разброса, среднее. С одной стороны математическое ожидание – это точка на числовой оси, а с другой – это правило (оператор), по которому определяется абсцисса этой точки. Оператор математического ожидания обозначается буквами «E » или «M », после которой в скобках стоит имя случайной величины:
 – дискретная СВ (ДСВ);
– дискретная СВ (ДСВ);
E (X) = M (X) = (51)
 – непрерывная СВ (НСВ).
– непрерывная СВ (НСВ).
Если последовательность  или интеграл в (51) сходятся, то математическое ожидание существует. Как оператор, математическое ожидание обладает определенными свойствами:
или интеграл в (51) сходятся, то математическое ожидание существует. Как оператор, математическое ожидание обладает определенными свойствами:
1) E (C) = C; 2) E (CX) = C ∙ E (X); 3) E (C + X) = C + E (X). (52)
Здесь C – константа. Доказательства свойств математического ожидания легко выполняются для дискретной случайной величины. Поясним физико-математический смысл свойств математического ожидания.
Первое свойство утверждает, что постоянная величина «С » сама себе является центром рассеивания. Её можно трактовать как дискретную случайную величину, имеющую единственно возможное значение, являющееся достоверным событием с вероятностью единица, т.е. E (C) = = C ∙1= C. Следствием этого свойства является равенство
E (E (X)) = E (X).
Второе свойство описывает реакцию случайной величины на изменение её единицы масштаба в «С» раз и предлагает заменять старое значение математического ожидания другим, пропорционально коэффициенту «C », вместо повторного выполнения вычислений по формулам (51).
Третье свойство математического ожидания показывает, что при переносе начала координат на величину С для получения нового значения этой характеристики достаточно добавить постоянную С к «старому» математическому ожиданию.
Все свойства можно представить в виде обобщённого свойства математического ожидания случайной величины, когда она подвергается линейному преобразованию:
E (C 1 + C 2 ∙ X) = C 1 + C 2 ∙ E (X) (53)
Определим дополнительно математическое ожидание некоторой функции φ(X) случайной величины X:
 – ДСВ;
– ДСВ;
E (φ(X)) = (54)
 – НСВ.
– НСВ.
Термин «математическое ожидание » говорит о том, что в результате эксперимента, скорее всего, будет наблюдаться один из элементов спектра случайной величины, близкий к центру рассеивания. Однако для некоторых распределений этого не происходит, а у других законов математическое ожидание как оператор не даёт числового значения. В подобных ситуациях можно рекомендовать другие характеристики положения: моду (Mo) или медиану (Me).
Для дискретных и непрерывных случайных величин мода определяется по-разному:
arg(P (X =Mo) = max) – ДСВ,
Mo(X) = (55)
arg(f (Mo) = max) – НСВ.
Если СВ имеет один максимум, то такое распределение называют унимодальным. Если же кроме абсолютного максимума имеются и локальные, то распределение называют полимодальным. Иллюстрации приведены на рисунках (Рис. 2.16 и 2.17).
| p pi - pi =max - p 1- 0 x 1 x 2 Mo xn -1 xnX |
| |||||
| Рис. 2.16 Унимодальность | Рис. 2.17 Бимодальность |
Медиана случайной величины – это такой элемент её спектра, относительно которого одинаково часто встречаются как б о льшие, так и м е ньшие значения, т.е. P (X > Me) = P (X < Me) = F (Me) = 1/2. Ордината, проходящая через медиану, делит площадь под кривой плотности пополам. Медиану определяют только для непрерывных случайных величин:
Me = arg(F (x) = 1/2).
На графике функции распределения (Рис. 2.18) дана соответствующая иллюстрация.
| F (x) |
| 1.0 |
| X |
| 0.5 |
| Me |
Рис. 2.18 Определение медианы СВ.
2.2.5.2 Моменты случайной величины.
Для обобщённых характеристик случайной величины используются начальные, центральные и абсолютные центральные моменты, в которых в качестве произвольной функции φ(x) (54) используется степенная функция случайного аргумента X.
Начальный момент порядка «r »:
 – ДСВ;
– ДСВ;
a r = E (Xr) = (56)
 – НСВ.
– НСВ.
Центральный момент порядка r:
 – ДСВ;
– ДСВ;
m r = E ( ) = (57)
) = (57)
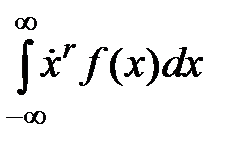 – НСВ,
– НСВ,
где  = X – E (X) – это уклонение СВ от ее центра рассеивания, называемое центрированным значением, случайным отклонением или флуктуацией. Для дискретной случайной величины сначала находится её математическое ожидание, а затем каждый элемент спектра xi «центрируется», т.е. из него вычитается значение величины E (X):
= X – E (X) – это уклонение СВ от ее центра рассеивания, называемое центрированным значением, случайным отклонением или флуктуацией. Для дискретной случайной величины сначала находится её математическое ожидание, а затем каждый элемент спектра xi «центрируется», т.е. из него вычитается значение величины E (X):  i = xi – E (X).
i = xi – E (X).
Абсолютный центральный момент порядка r:
 – ДСВ;
– ДСВ;
t r =  = (58)
= (58)
 – НСВ.
– НСВ.
Особый интерес представляют моменты первых четырех порядков, некоторые из которых имеют собственные имена. С вычислительной точки зрения нахождение начальных моментов менее объёмно, чем центральных. В связи с этим, для центральных моментов приводятся их выражения через начальные, что упрощает нахождение первых. Ниже представлена таблица первых пяти моментов от нулевого до четвёртого порядка включительно. Таблица включает в себя вышеупомянутые формулы связи центральных моментов с начальными. (Табл. 2.1).
Основные моменты СВ.
Табл. 2.1
| Порядок r | Моменты | ||
| Начальные a r | Центральные m r | Абс. центр. t r | |
| a0 ≡ 1 a1 = E (X) (мат.ожид.) a2 = E (X 2) a3= E (X 3) a4= E (X 4) | m0≡1 m1 ≡0 m2 =s2=a2–a12 (дисперсия) m3=a3–3 a2 a1+ +2 a13; m4=a4–4 a3 a1+ +6 a2 a12 –3 a14 | t0≡1 t1 = E (| ẋ |) (ср. откл.) t2 =m2 t3=E(| ẋ |3) t4=m4 |