Аналитические методы шифрования
Для шифрования информации могут использоваться аналитические преобразования. Наибольшее распространение получили методы шифрования, основанные на использовании матричной алгебры. Зашифрование k-го блока исходной информации, представленного в виде вектора Bk = ||bj||, осуществляется путем перемножения матрицы-ключа А = ||aij|| и вектора Bk. В результате перемножения получается блок шифртекста в виде вектора Ck = ||ci||, где элементы вектора Ck определяются по формуле:
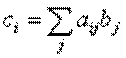
Расшифрование информации осуществляется путем последовательного перемножения векторов Ck и матрицы A-1, обратной матрице A.
Пример шифрования информации с использованием алгебры матриц.
Пусть необходимо зашифровать и расшифровать слово
Т0 = < ЗАБАВА> с помощью матрицы-ключа А:
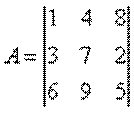
Для зашифрования исходного слова необходимо выполнить следующие шаги.
Шаг 1. Определяется числовой эквивалент исходного слова как последовательность соответствующих порядковых номеров букв слов Тэ:
Tэ = <8, 1, 2, 1, 3, 1>
Шаг 2. Умножение матрицы А на векторы В1 = {8, 1, 2} и В2 = {1, 3, 1}:
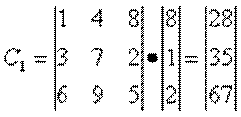 ;
;
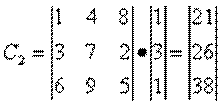 .
.
Шаг 3. Зашифрованное слово записывается в виде последовательности чисел Т1 = <28, 35, 67, 21, 26, 38>.
Расшифрование слова осуществляется следующим образом.
Шаг 1. Вычисляется определитель |А| = -115.
Шаг 2. Определяется присоединенная матрица А*, каждый элемент которой является алгебраическим дополнением элемента матрицы А
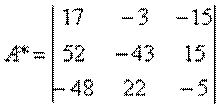 .
.
Шаг 3. Получается транспонированная матрица АT
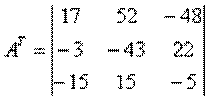 .
.
Шаг 4. Вычисляется обратная матрица А-1 по формуле:
А-1 = АТ/|А|.
В результате вычислений обратная матрица имеет вид:
 .
.
Шаг 5. Определяются векторы B1 и B2:
B1 = A-1*C1; B2 = A-1*C2.
 ,
,
 .
.
Шаг 6. Числовой эквивалент расшифрованного слова
|
|
Тэ = <8, 1, 2, 1, 3, 1> заменяется символами, в результате чего получается исходное слово Т0 = <ЗАБАВА>.
Методы аналитических преобразований
Шифрование методами аналитических преобразований основано на понятии односторонней функции. Будем говорить, что функция у=f(х) является односторонней, если она за сравнительно небольшое число операций преобразует элемент открытого текста х в элемент шифртекста у для всех значений х из области определения, а обратная операция (вычисление x=F**-1(y) при известном шифртексте) является вычислительно трудоемкой.
В качестве односторонней функции можно использовать следующие преобразования:
· умножение матриц;
· решение задачи об укладке ранца;
· вычисление значения полинома по модулю;
· экспоненциальные преобразования и другие.
Метод умножения матриц использует преобразование вида:
Y=C*X.
где Y=||y1,y2,...,yn||**Т, С=||Cij||, X=||x1,x2,...,xn||
Пример 1. Открытый текст: "ПРИКАЗ" ("16 17 09 11 01 08" согласно таблице 1).
Матрица С:
¦1 3 2¦
¦2 1 5¦
¦3 2 1¦
¦1 3 2¦ ¦16¦
¦2 1 5¦ X ¦17¦ =¦85 94 91¦
¦3 2 1¦ ¦09¦
¦1 3 2¦ ¦11¦
¦2 1 5¦ X ¦01¦ = ¦30 63 43¦
¦3 2 1¦ ¦08¦
Шифтекст: "85 94 91 30 63 43".
Задача об укладке ранца формулируется следующим образом. Задан вектор С=|c1,c2,...,cn|, который используется для шифрования сообщения, каждый символ si которого представлен последовательностью из n бит si=|x1,x2,...,xn|**t, Xk пp. {0,1}. Шифртекст получается как скалярное произведение С*si.
Пример 2. Открытый текст: "ПРИКАЗ" ("16 17 09 11 01 08" согласно таблице 1). Вектор С={1,3,5,7,11}.
Запишем код каждой буквы открытого текста в двоичном виде, используя пять разрядов.
П Р И К А З
100000 10001 01001 01011 00001 01000
Произведем соответствующие операции:
y1=1*1=1
y2=1*1+1*11=12
y3=1*3+1*11=14
y4=1*3+1*7+1*11=21
у5=1*11=11
y6=1*3=3.
Шифртекст: "01 12 14 21 11 03".
|
|
Метод полиномов основан на преобразовании
yi=xi**n+a1*xi**(n-1)+...+an(mod р).
где n, а1,а2...аn- целые неотрицательные числа, не превосходящие р, 1<=хi,уi<=р;
р - большое простое число.
Пример 3. Открытый текст: "ПРИКАЗ" ("16 17 09 11 01 08" согласно таблице 1).
Полином: уi=xi**3+2xi**2+3xi+4(mod 991).
y1=16**3+2*16**2+3*16+4(mod 991)=696
y2=17**3+2*17**2+3*16+4(mod 991)=591
у3=9**3+2*9**2+3*9+4(mod 991)=922
у4=11**3+2*11**2+З*11+4(mod 991)=619
y5=1**3+2*1**2+3*1+4(mod 991)=10
у6=8**3+2*8**2+З*8+4(mod 991)=668.
Шифртекст: "696 591 922 619 010 668".
Экспоненциальный шифр использует преобразование вида
уi =a**(xi) (mod р),
где хi- целое, 1<=хi<=р-1;
p - большое простое число;
a - целое, 1<=a<=p.
Пример 4. Открытый текст: "ПРИКАЗ"
("16 17 09 11 01 08" согласно таблице 1); a=3; p=991.
y1=3**16(mod 991)=43046721 (mod 991)=654
у2=З**17(mod 991)=129140163(mod 991)=971
у3=3**9(mod 991) = 19683 (mod 991) =854
y4=3**11(mod 991)=177147(mod 991)=749
у5=3**1 (mod 991)=3
y6=3**8 (mod 991)=6561 (mod 991)=615.
ШиФртекст: "654 971 854 749 003 615".
Особым случаем метода аналитических преобразований является метод, основанный на преобразовании
yi=xi ++ hi
где уi- i-й символ шифртекста;
хi- i-й символ открытого текста;
hi- i-й символ гаммы;
++ - выполняемая операция (наложение гаммы).
Различают два случая: метод конечной гаммы и метод бесконечной гаммы. В качестве конечной гаммы может использоваться фраза, а в качестве бесконечной - последовательность, вырабатываемая датчиком псевдослучайных чисел.
Пример 5. Открытый текст: "ПРИКАЗ" ("16 17 09 11 01 08" согласно таблице 1).
Гамма: "ГАММА" ("04 01 13 13 01").
Операция: сложение по mod 33.
y1= 16+4(mod 33)=20
y2= 17+1(mod 33)=18
y3= 9+13(mod 33)=22
y4= 11+13(mod 33)=24
y5= 1+1(mod 33)=2
y6= 8+4(mod 33)=12.
Шифртекст: "УСХЧБЛ" ("20 18 22 24 02 12").
|
|
Пример 6. Открытый текст: "ПРИКАЗ" ("16 17 09 11 01 08" согласно таблице 1).
Первые значения датчика: "21794567".
Операция: сложение по mod 2.
Запишем код каждой буквы открытого текста в двоичном виде, используя пять разрядов, а каждую цифру гаммы - используя четыре разряда:
16: 10000; 17: 10001; 09: 01001; 11: 01011; 01: 00001; 08: 01000
2: 0010; 1: 0001; 7: 0111; 9: 1001; 4: 0100; 5: 0101; 6: 0110; 7: 0111
Далее идет наложение до пятого разряда поочередно (для цифр гаммы):
10000 10001 01001 01011 00001 01000
++
00100 00101 11100 10100 01010 11001
=
10100 10100 10101 11111 01011 10001.
Шифртекст: "УУФЮКР".
УПРАЖНЕНИЯ.
1. Предложите свой шифр на основе аналитического преобразования. Укажите его достоинства и недостатки.
2. Зашифровать методом умножения матриц. Открытый текст: "Неделя", матрица С:
| 3 1 2 |
| 1 2 3 |
| 2 5 1 |
3. Открытый текст: "Неделя", вектор С={1,3,5,7,13}. Зашифровать, используя метод из примера 2.
4. Методом полиномов зашифровать. Открытый текст: "Монета"; полином: yi=xi**4+3*xi**3+2*xi**2+xi+3(mod991).
5. Используя экспоненциальный метод, зашифровать открытый текст: "Монета", а=2, p=991.
6. Используя метод конечной гаммы, зашифровать открытый текст: "Виноград", гамма: "дрова", операция: сложение по mod33.
7. Используя метод бесконечной гаммы, зашифровать открытый текст: "Виноград", первые показания датчика: 76549712321, операция: сложение по mod2.