Проекций
Сущность способа замены плоскостей проекций заключается в том, что одну из плоскостей проекций П 1 и П 2 (или последовательно обе) заменяют новой плоскостью, перпендикулярной к оставшейся. Положение заданных геометрических фигур в пространстве при этом не изменяется. Новую систему двух взаимно перпендикулярных плоскостей проекций выбирают так, чтобы заранее графические элементы (точки, линии, плоские фигуры) заняли положение, удобное для решения задачи.
Задача 4. Определить натуральную величину угла между гранями ACD и BCD (Рис. 4).
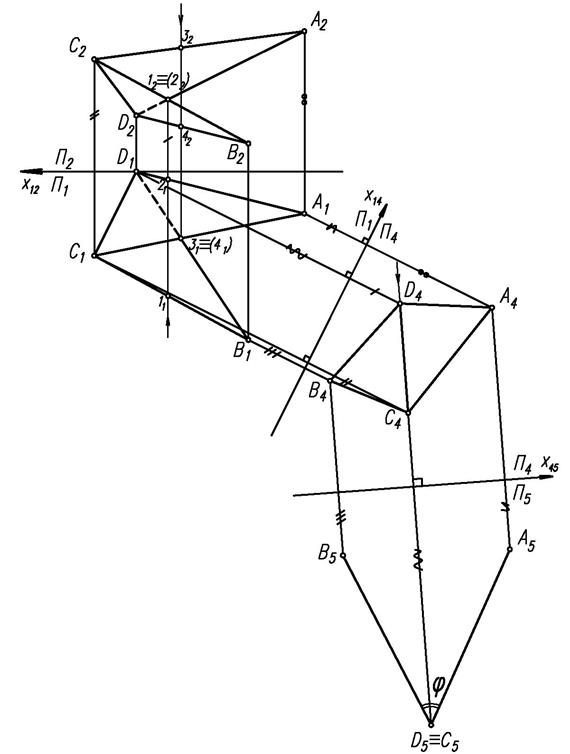
Рис. 4
Для определения натуральной величины двугранного угла чертеж необходимо преобразовать так, чтобы ребро СD спроецировалось в точку. Тогда двугранный угол спроецируется в линейный, величина которого и будет мерой двугранного угла.
Построение.
Рассматриваемую задачу можно решить двукратным преобразованием. Вначале заменой фронтальной плоскости проекций П 2 преобразуем чертеж так, чтобы ребро СD стало параллельным новой плоскости проекций П 4. Затем проводим еще одну замену плоскостей проекций, расположив новую плоскость проекций П 5 перпендикулярно ребру СD. На плоскость П 5 ребро СD спроецируется в точку, двугранный угол преобразуется в искомый линейный угол.
1. Заменяем плоскость проекций П 2 на новую плоскость проекций П 4, перпендикулярную плоскости П 1 и одновременно параллельную ребру СD. На чертеже ось х14 проводим параллельно горизонтальной проекции ребра СD – отрезку С 1 D 1.
2. Через точки А 1, В 1, С 1, D 1 проводим линии проекционной связи, перпендикулярные к новой оси х14 и откладываем на них отрезки, равные расстоянию от заменяемых проекций точек А 2, В 2, С 2, D 2 до предыдущей оси х12. Эти отрезки отмечены на чертеже символами – «/», «//», « ».
».
3. На новую плоскость проекций П 4 отрезок С 4 D 4 спроецируется в свою натуральную величину, так как он параллелен этой плоскости.
4. Заменим плоскость проекций П 1 на плоскость проекций П 5, перпендикулярную как плоскости П 4, так и ребру СD двугранного угла. На чертеже новую ось проекций х45 проведем перпендикулярно к проекции ребра СD – прямой С 4 D 4.
5. Строим новую проекцию А 5 С 5 D 5 В 5 всей фигуры двугранного угла. Для этого через точки А 4, В 4, С 4, D 4 проводим линии проекционной связи, перпендикулярные к новой оси х45. Откладываем на них отрезки, равные расстоянию от заменяемых проекций точек А 1, В 1, С 1, D 1 до предыдущей оси х14. Проекция ребра СD вырождается в точку, т.е.  .
.
6. Искомый угол φ между гранями АСD и ВСD определяется линейным углом между проекциями отрезков В 5 С 5(D 5) и А 5 С 5(D 5).
Задача 5. Определить расстояние от вершины А до грани BCD (Рис. 5).
Для решения этой задачи необходимо преобразовать чертеж так, чтобы грань, заданная треугольником ВСD, заняла проецирующее положение в новой системе плоскостей проекций.
Расстояние d от точки А до грани определяется величиной перпендикуляра, опущенного из точки А на плоскость треугольника ВСD. На новой плоскости проекций П 4 это расстояние спроецируется в свою натуральную величину (н.в. d).
Построение.
Заменой фронтальной плоскости проекций П 2 на новую плоскость проекций П 4 преобразуем чертеж так, чтобы грань ВСD заняла проецирующее положение по отношению к плоскости проекций П 4. Для этого необходимо выполнить следующие преобразования.
1. Через вершину D проведем горизонталь треугольника ВСD.
2. Заменим плоскость П2 на новую плоскость проекций П 4, перпендикулярную как плоскости П 1, так и плоскости треугольника ВСD. На чертеже новую ось проекций х14 проведем перпендикулярно к горизонтальной проекции горизонтали h 1.
3. Строим проекции точки А и вершин треугольника ВСD на плоскость проекций П 4. Для этого из точек А 1, В 1, С 1, D 1 проводим линии проекционной связи, перпендикулярные к новой оси х14 и откладываем от новой оси отрезки, равные расстоянию от заменяемых проекций точек А 2, В 2, С 2, D 2 до оси х12. Проекция треугольника ВСD вырождается на плоскости П 4 в отрезок прямой линии (В 4 D 4 С 4), так как треугольник  .
.

Рис. 5
4. Опустим перпендикуляр d из точки А на плоскость треугольника ВСD. Найдем точку К основания перпендикуляра. На чертеже проекция перпендикуляра А 4 К 4 перпендикулярна вырожденной проекции (В 4 D 4 С 4) треугольника ВСD.
5. Отрезок А 4 К 4 определяет расстояние от точки А до грани ВСD (А 4 К 4= н.в. d). На плоскость П 4 он спроецируется без искажения.
Задача 6. Определить натуральную величину грани ВСD (Рис. 6).
Для определения натуральной величины грани ВСD необходимо последовательно провести еще одну замену плоскостей проекций, расположив плоскость П 5 параллельно треугольнику ВСD. На плоскость П 5 треугольник спроецируется в свою натуральную величину.
Построение.
При решении предыдущей задачи чертеж был преобразован так, что плоскость треугольника ВСD стала проецирующей по отношению к новой плоскости проекций П 4. Для дальнейших построений необходимо выполнить следующие действия.
1. Заменим плоскость П 1 на новую плоскость проекций П 5, перпендикулярную плоскости П 4 и одновременно параллельную плоскости треугольника ВСD. На чертеже ось х45 проведем параллельно вырожденной проекции треугольника ВСD – отрезку (В 4 D 4 С 4).
2. Через точки В 4, С 4, D 4 проведем линии проекционной связи, перпендикулярные к новой оси х45 и отложим на них отрезки, равные расстоянию от заменяемых проекций точек В 1, С 1, D 1 до предыдущей оси х14. Эти отрезки отмечены на чертеже символами: «///», « » и др.
» и др.
3. На новую плоскость проекций П 5 треугольник ВСD спроецируется в натуральную величину, так как он параллелен этой плоскости.
Компоновка и выполнение листа 2 самостоятельной графической работы с задачами 4, 5, 6 приведены в приложении 3 (Рис. 8).

Рис. 6