Изменение проводимости между истоком и стоком при интерференции транзистора.

Интерференционные транзисторы

Электронные приборы, приведенные в данном подразделе, основаны на интерференции электронных волн и баллистическом транспорте носителей за­ряда. Для них значимой мерой протяженности активной области является дли­на фазовой когерентности. При этом в приборных структурах с размерами ак­тивных областей меньше длины фазовой когерентности электронных волн мо­гут присутствовать и эффекты, связанные с размерным квантованием. Однако эти сопутствующие эффекты в данном случае являются эффектами второго порядка.

Электроны в некоторых полупроводниках способны поддерживать фазо­вую когерентность на длине в несколько микрон. Перенос электронов через об­ласти меньше, чем длина фазовой когерентности, контролируется испытывае­мой ими интерференцией. Если управлять интерференцией с помощью какого- либо внешнего механизма, например, через управляющий электрод - затвор, получим квантовый интерференционный транзистор (quantum interference transistor). Предложено два принципиальных типа конструкций квантовых ин­терференционных транзисторов. Один из них является развитием идеи элек­тронного согласующего волновода, в другом же используется принцип кольце­вого интерферометра.

Квантовые интерференционные транзисторы, основанные на электронном согласующем волноводе, были проанализированы Солсом (1989) и Даттом (1989). Оба рассматривали трехвыводные приборы, в которых эффективная длина волновода может варьироваться с помощью внешнего затвора. Соответ­ствующая конструкция показана на рис. 1.9,а.

Рис.1.9. Численное моделирование, демонстрирующее геометрию прибора (а) и пропускание в случае одной заполненной подзоны (б) и множества заполненных подзон (в).

Ток может течь от истока к стоку либо непосредственно (по коротким траекториям), либо по более длинным пу­тям через волновод. Разность хода (расстояние) между двумя путями прохож­дения тока может регулироваться с помощью затвора. Электронные волны, ес­ли только они не испытывают никаких изменяющих их фазу столкновений, достигая стока по двум разным путям, будут конструктивно интерферировать (складываться) всякий раз, когда разность хода равна целому числу длины вол­ны Ферми, которая составляет порядка 50 нм в двухмерном электронном газе. Конструктивная интерференция локализует электроны на выходе согласующе­го волновода, и проводимость между истоком и стоком увеличивается.

Для прибора, в активной области которого электронами заполнен только один энергетический уровень (или одна подзона), проводимость между истоком и стоком может модулироваться между многократными состояниями «включе­но» - «выключено», изменением разности хода L только на несколько элек­тронных длин волн, как показано на рис.1.9,б.

Однако для прибора, в котором заполнено более чем одно энергетическое состояние (более чем одна подзона), однородной электронной длины волны не существует. Вместо этого каждая мода распространяется со своей собственной длиной волны и вообще не будет разности хода, для которой могут быть дос­тигнуты или аддитивная (усиливающая), или ослабляющая интерференция. В результате модуляция проводимости будет меньше 100% (рис.1.9,в) и быстро ухудшается с увеличением индекса моды. Ясно, что эффективно работать мо­жет лишь одномодовый прибор.

Кольцевой интерференционный транзистор был предложен Фаулером (1984). Он рассмотрел кольцевую конструкцию, в которой одну половину коль­ца пересекает затвор, имеющий короткую область, составляющую часть его полной длины, ΔL, как показано на рис. 1.10. Затвор может быть использован для изменения электронной плотности, в результате чего получается различная энергия Ферми и, следовательно, длина волны Ферми для электронов под затвором. Это приведет к разности хода между электронными волнами, которые распространяются через различные ветви конструкции.

Рис.1.10. Кольцевая конструкция электронного интерференционного транзистора.

Электроны из различных ветвей конструкции покидают кольцо в одной и той же точке, и, если разность фаз равна 2π, они будут аддитивно интерфериро­вать и проводимость кольца будет максимальной. Следовательно, проводи­мость кольца может быть сделана осциллирующей с периодом волнового век­тора Ферми, задаваемым уравнением

(kF – k’F)ΔL=2πn,

где kF - волновой вектор в области длины ΔL под затвором и n - целое число. Как в случае с согласую­щим волноводом, модуляция может в принципе достигать 100 % для одномодо­вых колец.

Форд и другие (1990) позаимствовали похожий подход, но в их геометрии плечи кольца имеют различную длину и вся структура целиком управляется за­твором. Условие интерференции становится таким: kFΔL =2πn, и kF изменяется посредством изменения напряжения затвора.

Интерес к квантовому интерференционному транзистору связан с тем, что он может быть быстродействующим прибором с большим коэффициентом усиления. Высокое быстродействие осуществляется главным образом благода­ря малым размерам. Скорость движения электронов в GaAs равна около 105 м/с, и поэтому, время переноса носителей зарядов (время пролета) через активную область протяженностью 100 нм составляет всего 10-12 с. Конечно, как и в обычных полевых транзисторах, максимальная рабочая частота будет огра­ничиваться паразитными параметрами, такими как время зарядки RC-цепочки затвора. На практике быстродействие квантового интерференционного транзи­стора почти такое же, как у короткоканальных полевых транзисторов, их пре­имущество связано с потенциально высокой крутизной характеристики прямой передачи.

Вместе с этим следует иметь в виду и факторы, ограничивающие практи­ческое применение интерференционных транзисторов. Это в первую очередь низкие рабочие температуры, что диктуется необходимостью отсутствия рас­сеяния носителей заряда в рабочей области прибора. Даже на чистых материа­лах при нанометровых размерах рабочих областей приемлемые условия по длине фазовой когерентности удается реализовать практически лишь при тем­пературах порядка 70 -100 К. Другим существенным ограничением является требование одномодовости проводящего канала. Это приводит к тому, что ра­бочие токи в интерференционных транзисторах должны быть очень маленьки­ми. Как следствие, такие приборы нуждаются в дополнительных усилителях и имеют очень низкую помехоустойчивость. Названные ограничения пока сдер­живают применение интерференционных транзисторов в современных инте­гральных схемах.

14 Туннульные эффекты. Взаимодействие квантовых частиц с потенциальными барьерами. Квантовые ограничения на туннелирование.

Туннельный эффект, туннелирование — преодоление микрочастицей потенциального барьера в случае, когда её полная энергия (остающаяся при туннелировании неизменной) меньше высоты барьера. Туннельный эффект — явление исключительно квантовой природы, невозможное в классической механике и даже полностью противоречащее ей. Аналогом туннельного эффекта в волновой оптике может служить проникновение световой волны внутрь отражающей среды (на расстояния порядка длины световой волны) в условиях, когда, с точки зрения геометрической оптики, происходит полное внутреннее отражение. Явление туннелирования лежит в основе многих важных процессов в атомной и молекулярной физике, в физике атомного ядра, твёрдого тела и т. д.

Потенциальный барьер – область пространства, где потенциальная энергия частицы (или тела) выше, чем в соседних областях. Рассмотрим простейший потенциальный барьер прямоугольной формы шириной а и высотой U0. Вне барьера потенциальная энергия частицы равна нулю. Полная энергия частицы Е равна сумме её кинетической энергии Т и потенциальной U. Вне барьера Е = Т. Если частица двигается на барьер слева и имеет Е = Т < U0, то с точки зрения классической физики она не может преодолеть его и отразится от него. Действительно, классическая физика требует безусловного сохранения энергии. Если представить, что частица с Е< U0, вошла внутрь барьера, то она неизбежно должна иметь там отрицательную кинетическую энергию (чтобы её полная энергия сохранилась), что невозможно по смыслу кинетической энергии.

С точки зрения квантовой физики частица с Е< U0 может с некоторой вероятностью пройти сквозь барьер. Это явление носит название туннельного эффекта.

Вероятность прохождения частицы массы m через барьер D определяется соотношением

где.

Основная зависимость коэффициента прохождения D от ширины a и высоты барьера U0 определяется экспоненциальным множителем e-χa.

В случае a ~ 10-13 см, m ~ 10-24 г для (U0 − E) ~ 10 МэВ D ~ 1/e.

То есть частица (протон, α-частица) с заметной вероятностью может пройти сквозь потенциальный барьер, превышающий её энергию на 5–10 МэВ.

15.Одноэлектронноетуннелирование носителей заряда в условиях кулоновской блокады.Одно Одноэлектронный транзистор.

Одноэлектронное туннелирование

В лекции 1 мы рассказывали о туннельном токе между наноразмерным острием металлического зонда и электропроводящим образцом. В общем случае речь идет о том, что в квантовой механике частица описывается как волна, "облако", распределенное по всей области пространства, где ее волновая функция отлична от нуля. И есть определенная вероятность найти микрочастицу в любой точке этого пространства, даже там, куда по классическим представлениям она никак не может попасть. Поэтому в ряде случаев частица может проникать сквозь потенциальные барьеры, проходя словно сквозь "туннели" в них. В силу этого случаи такого просачивания называют "туннельным эффектом". Многочисленные эксперименты и практические применения доказали правоту в этом вопросе именно квантовой, а не классической механики.

Кулоновская блокада

В наноэлектронике туннельный эффект чаще всего используют для прохождения электронов проводимости сквозь тонкий (порядка 1-10 нм) слой изолятора между двумя проводниками ("туннельный переход", рис. 3.6.а). Энергетическая диаграмма для этой системы такая же, как показано в лекции 1 на рис. 1.3 справа, лишь "Вакуум" надо заменить на диэлектрик, а "Зонд" и "Образец" – на электроды Эл1 и Эл2. Как и там, "прозрачность" вакуумного барьера и туннельный электрический ток описываются выражением (1.2), т.е. зависимость их от толщины барьера, а также от работы выхода () является приблизительно экспоненциальной.

Рис. 3.6.

а) Структура туннельного перехода. Справа – временные диаграммы: б) включения напряжения; в,г) электрического тока и напряжения на переходе, когда напряжение мало; д,е) напряжения на переходе и электрического тока, когда приложенное напряжение превышает UК. ж) Зависимость среднего тока сквозь туннельный переход от приложенного напряжения

Когда хотя бы один из электродов имеет площадь порядка единиц квадратного нанометра, тогда электрическая емкость между электродами оказывается очень малой, и наблюдаются особые явления. Ведь для перемещения электрона из электрода Эл1 на электрод Эл2 надо выполнить работу против сил кулоновского притяжения. Наибольшая работа, которую способен выполнить источник напряжения по перемещению электрического заряда , равна . Поэтому для того, чтобы электрон мог перейти из электрода Эл1 на электрод Эл2, должно быть выполнено условие

(3.19)

Потенциал

(3.20)

называют "кулоновским потенциалом" или "кулоновским зазором" (англ. Coulombgap).

На рис. 3.6.б показана временная диаграмма включения источника напряжения, на рис. 3.6.в – ток зарядки емкости после включения напряжения, на рис. 3.6.г – изменение напряжения на емкости в случае, когда условие (3.19) не выполняется. В результате протекания кратковременного тока емкость заряжается до потенциала , и дальнейшее протекание тока прекращается. Это состояние называют "кулоновской блокадой" (англ. Coulombblockade). Она становится заметной лишь в наноэлектронике. Ведь даже при емкости туннельного перехода в 1 пФ кулоновский потенциал составляет лишь 80 нВ. А вот при емкости 10-18 Ф имеем уже = 80 мВ, что легко заметить.

Важной является и температура окружающей среды. Ведь кулоновскую блокаду можно наблюдать и использовать лишь при условии, когда кулоновская энергия намного превышает энергию хаотического теплового движения электронов

(3.21)

Это условие выполняется притем более высоких температурах, чем меньше емкость туннельного перехода. А она зависит от размеров электродов.

Одноэлектронные колебания

На рис. 3.6.д показана временная диаграмма изменения напряжения UC2 на емкости после включения источника напряжения в случае, когда . Емкость начинает заряжаться, но как только напряжение на ней превышает , происходит туннелирование одного электрона, и напряжение на емкости прыжком падает до значения . Под действием источника напряжения емкость снова начинает заряжаться, но как только напряжение на ней превышает , снова происходит туннелирование одного электрона, и напряжение на емкости прыжком падает до . Этот процесс повторяется все время, пока включен источник напряжения. Соответствующие временные изменения тока через туннельный переход показаны на рис. 3.6.е. Туннельный переход периодически генерирует очень короткие импульсы тока. Длительность этих импульсов можно оценить из соотношения неопределенности

(3.22)

где – постоянная Планка (4,14*10-15 эВ*с), – высота туннельного барьера, в данном случае – работа выхода электрона. Если она составляет приблизительно 4 эВ, то с. Периодические импульсы тока, которые сопровождают перенос каждого отдельного электрона через наноразмерный туннельный барьер, называют "одноэлектронными колебаниями". Частота этих колебаний в принципе может достигать 100 ТГц и выше. Она ограничивается лишь паразитными емкостями, электрическим сопротивлением и индуктивностями схемы.

На рис. 3.6.ж показана вольтамперная характеристика наноразмерного туннельного барьера – зависимость среднего (по времени) электрического тока от приложенного напряжения. Если материал электродов Эл1 и Эл2 одинаков, то ВАХ является симметричной.

Кулоновская лестница

Интересным оказался случай двойного туннельного барьера (рис. 3.7.а), когда наноостровок НО из металла или полупроводника находится в диэлектрике Д между двумя электродами Эл1 и Эл2 и отделен от них тонкими туннельными барьерами. Если материалы электродов и ширина обоих барьеров приблизительно одинаковы, то ВАХ такой двойной туннельной структуры подобна ВАХ на рис. 3.6.ж, но, как правило, немного сдвинута в ту или другую сторону вдоль горизонтали (рис. 3.7.б). Это связано с начальным (при )

зарядовым состоянием наноостровка.

Рис. 3.7. а) Структура двойного туннельного барьера. б) ВАХ приблизительно одинаковых барьеров. в) ВАХ в случае существенно разных барьеров – "кулоновская лестница"

Если же туннельные барьеры с двух сторон наноостровка значительно отличаются (шириной или высотой), то наблюдается непривычная форма ВАХ, которую называют "кулоновской лестницей" (англ. Coulombstaircase). Она объясняется тем, что сквозь один из туннельных барьеров (например, левый) электроны туннелируют значительно легче. Поэтому на наноостровок из левого электрода может туннелировать второй электрон, когда первый еще не успел туннелировать из наноостровка на правый электрод.

Кулоновская потенциальная энергия наноостровка с двумя избыточными электронами равна , где – электрическая емкость островка. Поэтому для туннелирования на островок второго электрона надо выполнить работу

(3.23)

Это возможно, только если напряжение на туннельном барьере достигает значения, при котором

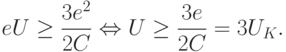
(3.24)

До выполнения этого условия имеет место кулоновская блокада. Поэтому после первой "ступеньки" ВАХ электрический ток через двойной туннельный барьер не увеличивается при росте напряжения до тех пор, пока не будет выполнено условие (3.24). После этого ток скачком возрастает, однако дальнейший рост тоже прекращается, пока не будет выполнено условие

(3.25)

Это объясняет вторую "ступеньку" на ВАХ. Когда выполняется условие (3.25), ток снова возрастает с повышением напряжения и т.д. Каждой "ступеньке" отвечает определенное число избыточных электронов на наноостровке: первой "ступеньке" – 1, второй – 2, третьей – 3 и т.д.

Одноэлектронный транзистор (— транзистор, в основе концепции которого лежит возможность получения заметных изменений напряжения при манипуляции с отдельными электронами. Такая возможность имеется, в частности, благодаря явлению кулоновской блокады.

Впервые о возможности создания одноэлектронных транзисторов на основе кулоновской блокады сообщили в 1986 г. советские учёные К. К. Лихарев и Д. В. Аверин. В 1996 г. российские физики С. П. Губин, В. В. Колесов, Е. С. Солдатов, А. С. Трифонов, В. В. Ханин, Г. Б. Хомутов, С. А. Яковенко впервые в мире создали одноэлектронный молекулярный нанокластерный транзистор, работающий при комнатной температуре.

Аналогично полевому полупроводниковому транзистору, одноэлектронный транзистор имеет три электрода: исток, сток и затвор. В области между электродами располагаются два туннельных перехода, разделённых дополнительным металлическим или полупроводниковым электродом с малой ёмкостью, который называется «островом». Остров представляет собой наночастицу или кластер нанометровых размеров, изолированный от электродов диэлектрическими прослойками, через которые и может при определённых условиях происходить движение электрона. Электрический потенциал острова может регулироваться изменением напряжения на затворе, с которым остров связан ёмкостной связью. Если приложить напряжение между истоком и стоком, то ток, вообще говоря, протекать не будет, поскольку электроны заблокированы на наночастице. Когда потенциал на затворе станет больше некоторого порогового значения, кулоновская блокада прорвётся, электрон пройдёт через барьер, и в цепи исток-сток начнёт протекать ток. При этом ток в цепи будет протекать порциями, что соответствует движению единичных электронов. Таким образом, управляя потенциалом на затворе, можно пропускать через кулоновские барьеры одиночные электроны. Количество электронов в наночастице должно быть не более 10 (а желательно и меньше). Это может быть достигнуто в квантовых структурах с размером порядка 10 нм.

Рассмотрим квантовые состояния электрона при разных потенциалах на затворе. В блокированном состоянии у электрона на истоке нет доступных энергетических уровней в пределах диапазона туннелирования (красная точка на рис. 2). Все уровни с меньшей энергией на острове заняты.

Когда к затвору прикладывается положительный потенциал, энергетические уровни на острове понижаются. Электрон (зелёный 1.) может туннелировать на остров (зелёный 2.), занимая свободный энергетический уровень. Отсюда он может туннелировать на сток (зелёный 3.), где он неупруго рассеивается и достигает на нём уровня Ферми (зелёный 4.).

Энергетические уровни на острове распределены равномерно; расстояние между ними () равно энергии, необходимой каждому последующему электрону для попадания на остров, обладающий ёмкостью . Чем ниже , тем больше . Для преодоления кулоновской блокады необходимо выполнение трёх условий:

напряжение смещения не может превышать энергии зарядки;

тепловая энергия 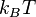должна быть ниже энергии зарядки , либо электрон должен пройти квантовую точку за счёт теплового возбуждения;

сопротивление туннелирования () должно быть больше, чем , которое вытекает из принципа неопределённости Гейзенберга.