| Группа сопротивлений | I-VIII | II-IX | X-XI | VIII-XII | |||||||||
| Участок сопротивлений | 1-2 | 2-3 | 3-4 | 4-5 | 5-6 | 6-7 | 7-а-8 | 8-9 | 3-11 | 10-11 | 11-12 | 9-13 | |
| Коэффициент сопротивления ζ | Колено α0, R/d Клапан запорный проходной Клапан невозвратно-запорный проходной Тройник Четверник Фильтр Кингстон приемный | ||||||||||||
| Σζ | |||||||||||||
| Расчетная скорость v, м/с | |||||||||||||
| Потеря напора hМ = Σζ · v2 / 2, Дж/кг | |||||||||||||
3.1.7. Вычисляется внутренний диаметр трубопровода на участке:
 . (5)
. (5)
3.1.8. Подбирается ближайший стандартный внутренний диаметр dгост1-2. Стандартом регламентируются следующие значения: Dу 10,15,20,32, 40, 50,65, 90,100,125,150,200,250,300,350,400 и др. – см. [1]. Расхождение не должно превышать 10%, в противном случае гидравлический расчет необходимо выполнять по фактическому внутреннему диаметру в соответствии с табл.5.
Таблица 5
| Наружный диаметр, мм | 50, 54, 57, 60; 63,5; 68, 70, 73, 76, 83, 89, 95, 102, 108, 114, 121, 127, 133, 140, 146, 152, 159, 168, 180, 194, 203, 219, 245, 273, 299, 325, 351, 377, 402, 426, 450, 480, 500, 530, 560, 600, 630, 720, 820 |
| Толщина стенки, мм | 2,5; 2,8; 3; 3,5; 4; 4,5; 5; 5,5; 6; 7; 8; 9; 10; 11; 12; 14; 16; 17; 18; 20; 22; 25; 28; 30; 32; 36; 40; 45; 50; 56; 60; 63; 70; 75 |
3.1.9. Уточняется скорость по выбранному диаметру:
 (6)
(6)
3.1.10. Рассчитывается критерий Рейнольдса:
 (7)
(7)
где ν (м2/с) – коэффициент кинематической вязкости перекачиваемой жидкости, взятый из [8, 13].
3.1.11. Определяется коэффициент гидравлического трения λ1-2 по одной из следующих формул для турбулентного режима:
– для гидравлически гладких труб при 2300 < Re < 105 – формула Блазиуса:

– то же при 105 < Re < 3 · 106 – формула Кольбрука
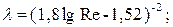
– для гидравлически шероховатых труб в области доквадратичного сопротивления при 10d / Δэ < Re < 500d / Δэ – формула Альтшуля
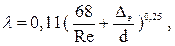
где Δэ – эквивалентная шероховатость, определяемая по справочнику [8].
– то же в области квадратичного сопротивления при Re > 500d / Δэ – формула Прандтля – Никурадзе:

3.1.12. Вычисляются потери напора от трения на участке:
 (8)
(8)
3.1.13. Подсчитывается потерянный напор на участке:
 (9)
(9)
3.1.14. Решается уравнение Бернулли для этого участка:

относительно напора Н2 = р2 / ρ; при этом учитывается, что v1 = v2 = v1-2; α1 = α2 = 1:
 (10)
(10)
Таким образом, напор в точке 2 определен, т.е. для участка 1-2 задача решена полностью и в конечном виде.
3.1.15. Дальнейшее заполнение основного бланка производится аналогично, последовательно по каждому участку и группе, в результате чего определяются узловые напоры. Узловой напор НУЗi находится как сумма узлового напора в предшествующей точке и потери напора между предшествующей и данной узловыми точками.
3.1.16. Узловые напоры в одной и той же точке, подсчитанные по основной магистрали НУЗМАГ и ответвлению НУЗОТВ , обычно не равны между собой. Если они различаются менее чем на 5%, то расчетный узловой напор принимается равным среднему арифметическому из двух значений НУЗСР. Если же различие более 5%, то напоры следует уравнять.
3.1.17. Для этого наиболее целесообразно изменить диаметр одного из ответвлений (в пределах обеспечения допустимых скоростей). При невозможности такого изменения в ответвление с меньшим сопротивлением устанавливается дроссельное устройство (диафрагма), расчет которого на бескавитационный режим течения см. [11].
3.1.18. В основной расчетный бланк заносится ΔН = Н УЗМАГ – Н УЗОТВ.
3.1.19. Подсчитывается напор в нагнетательном патрубке насоса, который равен сумме узлового напора последней точки основной магистрали и потерь напора между этой точкой и насосом:
Н9наг = Н8 + h8-9.
3.1.20. Рассчитывается сопротивление всасывающей магистрали от приемного отверстия до насоса аналогично напорному патрубку.
3.1.21. Определяется напор, развиваемый насосом, как алгебраическая разность полных напоров в нагнетательном и всасывающем патрубках:
НН = Н9НАГ – Н9ВС .
3.1.22.Подбирается насос по общей производительности QН и напору НН, которые определены расчетом. Характеристики и обозначение насоса записываются в отдельную форму основного бланка (см. табл.6).
Таблица 6
| Насос | ||
| Требуется | Принят | |
| QН , м3 / ч | НН, Дж / кг | Обозначение |
| … | … | … |
3.2. Решение обратной задачи аналитическим методом (рис.4, б)
3.2.1. Заданными являются: вид транспортируемой жидкости, характеристики насоса (производительность QН, напор НН) и параметры трубопровода (длины участков, тип и количество арматуры и фасонных частей). Требуется определить расходы по ответвлениям Qi и напоры Нi у потребителей.
3.2.2. Трубопровод на расчетной схеме разбивается на основную магистраль и ответвления от насоса к самой удаленной точке системы с указанием узлов и участков.
Основной и вспомогательный расчетные бланки аналогичны принятым при решении прямой задачи, но потери напора в дроссельных устройствах (если таковые имеются) рассчитываются на вспомогательном бланке наряду с потерями в других местных сопротивлениях.
3.2.3. Расчет начинают с основной магистрали I – IX, а затем рассчитывают отдельные ответвления. Приняв скорость движения жидкости в магистрали v1-2 в пределах 2÷4 м / с, определяют ее диаметр по формуле:
 (11)
(11)
3.2.4. Участки магистрали рассчитывают последовательно один за другим. Для участка 1-2 аналогично пунктам 3.1.8 ÷ 3.1.13 вычисляются потери напора h1-2.
3.2.5. Из уравнения Бернулли

находят:
Н2 = НН – h1-2 – (z2 – z1), Дж / кг. (12)
3.2.6. Аналогично рассчитывают участки 2–а–3, 3–4, 4–5, 5-6, 6–7, 7–8 и 8–9, определяя напоры в узловых точках III ÷ IX.
3.2.7. По известным напорам Н7 и Н8 выполняют расчеты ответвлений 7–11 и 8–10.
3.2.8. Для простого трубопровода (например, участок 8–10) задаются в первом приближении напором Н10 = Н ׳10 (Дж / кг) и вычисляют следующие величины:
– расход жидкости на участке:
Q'8-10 = μ S10  (13)
(13)
– скорость жидкости в трубопроводе:
v'8-10 = 4 Q'8-10 / π d 2 8-10, м / с, (14)
где диаметр ответвления d 8-10 предварительно назначается;
– число Рейнольдса:
Re'8-10 = v'8-10 d 8-10 / ν; (15)
– суммарный коэффициент сопротивления трубопровода:
ζ'8-10 = Σ ζ' + λ 8-10 l 8-10 / d 8-10; (16)
– потери напора на участке:
h'8-10 = ζ'8-10 v'28-10 / 2, Дж / кг; (17)
3.2.9. Решают задачу во втором приближении. Напор у потребителя будет равен:
Н"10 = Н 8 – h'8-10 – g (z 10 – z 8), Дж / кг (18)
3.2.10. Повторяют расчет по формулам (13) ÷ (17) в той же последовательности, как и в первом приближении. В результате получают Q"8-10, v"8-10, Re"8-10, ζ"8-10 и h"8-10. И так выполняют ряд последовательных приближений, пока не получат значения напора Н10 для всех двух последовательных приближений, близкие между собой.
3.2.11. Производят уравнивание узловых напоров (в случае необходимости) изменением расходов по ответвлениям [11].
3.2.12. Обратная задача может быть решена также графоаналитическим методом. Для этого задаются тремя произвольными значениями напоров у потребителя, например Н I 11, H II 11, H III 11 (Дж / кг), с таким расчетом, чтобы в принятый диапазон попадал действительный напор у потребителя.
3.2.13. Решают для каждого напора прямую задачу и находят соответствующий ему расход жидкости QI 7-11, QII 7-11, QIII 7-11. Полученные результаты обобщаются в виде графика Н11 = f (Q7-11) – cм. рис.5.
3.2.14. Зная истинный напор в узловой точке VII, по графику определяют расход на данном участке Q 7-11.
3.2.15. Далее следует аналитический расчет:
Q 7-11 → v 7-11 → Re 7-11 → λ 7-11; Σ ζ 7-11 → h 7-11 → H11.

Рис. 5. Характеристика участка (простого трубопровода)
Примечание. При выполнении гидравлических расчетов необходимо учитывать, что для параллельных участков разветвленного трубопровода (рис.6, а) справедливы следующие зависимости:
QΣ = Q1 + Q2 + Q3; НΣ = Н1 = Н2 = Н3.
Для последовательных участков (рис.6, б) имеем:
QΣ = Q1 = Q2 = Q3; НΣ = Н1 + Н2 + Н3.

Рис.6. Суммарные характеристики разветвленных трубопроводов
3.3. Решение прямой задачи методом потерянного напора на единицу длины трубопровода
3.3.1. Данный метод, называемый иначе методом эквивалентных длин, широко используется, например, при расчетах вентиляционных трубопроводов. Он основан на замене потерь напора в местных сопротивлениях равными потерями на трение воображаемого эквивалентного прямого трубопровода.
hМ = hТ или 
Отсюда эквивалентная длина: 
3.3.2. Суммарные потери напора составят
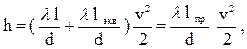 (19)
(19)
где:
l ПР = l + l ЭКВ (20)
называется приведенной длиной трубопровода.
3.3.3. Учитывая, что отношение потерь напора в трубопроводе к его длине представляет собой гидравлический уклон, окончательная расчетная формула будет иметь вид:
h = i l ПР. (21)
3.3.4. Расчет потерь напора по участкам выполняется в табличной форме (см. табл.7). Заданными считаются расход и допустимая скорость по потребителям, а также расчетная схема трубопровода системы (рис.4, а).
3.3.5. В таблицу вносят коэффициенты местных сопротивлений ζ по каждому участку и подсчитывают их сумму.
3.3.6. Определяют число Re, по которому вычисляют гидравлический уклон i на участке.
3.3.7. Находят полную эквивалентную и приведенную длины участка l ЭКВ и l ПР.
3.3.8. Определяют потери напора от трения и местных сопротивлений, а затем узловой напор в конце участка как сумму среднего узлового напора в предшествующей точке и потери напора между предшествующей и данной узловыми точками.
3.3.9. Подсчитывают необходимый напор в нагнетательном патрубке насоса, который равен сумме напоров последней узловой точки основной магистрали и потери напора от нее до насоса.
3.3.10. Аналогично вычисляют потери напора во всасывающем патрубке насоса.
3.3.11. Находят полный напор, развиваемый насосом, как разность напоров в патрубках.
Таблица 7