Очевидно, что основной предпосылкой является наличие окружности (ей). Подчёркиваю, что это лишь предпосылка, а не обязательное правило! То есть, область интегрирования может быть ограничена окружностью (ями), но переход к полярным координатам только усложнит решение, а то и вообще заведёт его в тупик. И такие примеры встречаются реально.
Итак, площадь фигуры вычислим с помощью двойного интеграла, используя полярную систему координат:
По формулам перехода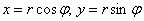 
найдём полярные уравнения окружностей:
Теперь выясним порядок обхода области. Луч радара входит в область через окружность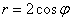 
и выходит из неё через окружность 
(красная стрелка), при этом он осуществляет поворот от полярной оси 
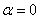до угла 
(зелёная стрелка).
Напомню также, что «альфа» и «бета» – это не просто формальные значения углов: полярное уравнение 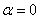непосредственно задаёт полярную ось (положительное направление оси абсцисс), а уравнение 
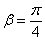– луч, исходящий из полюса и совпадающий с верхней частью прямой 
.
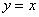Примечание: если рассматривать обобщенные полярные координаты, то уравнение 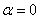определяет полярную ось и её продолжение (всю ось абсцисс), а уравнение 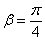– всю прямую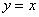
В рассматриваемой задаче дана «хорошая» прямая 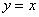и значение угла 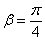понятно «с ходу». Как найти угол в общем случае? Из материалов статьи Прямая на плоскости вспоминаем, что угловой коэффициент прямой 
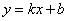равен тангенсу угла наклона данной прямой к положительному направлению оси абсцисс: 
. В данном случае 
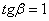, откуда следует, что 
(если тяжко с числами – тригонометрические таблицы в помощь).
Возвращаемся к решению. По результатам «сканирования» области мы выяснили, что на промежутке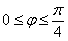 
полярный радиус изменяется в пределах 
.
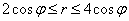Перейдём к повторным интегралам:
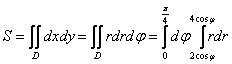
Остальное – дело техники:
1)
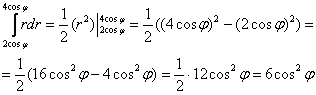
2)
Ответ: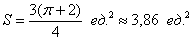 
Прикинув по чертежу количество клеточек, приходим к выводу, что полученный результат вполне и вполне правдоподобен.
Следующие два примера для самостоятельного решения:
Пример 3
С помощью двойного интеграла вычислить площадь фигуры, ограниченной линиями 
Пример 4
Вычислить двойной интеграл, используя полярные координаты
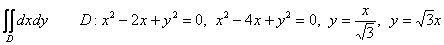
В примере №4 мы встретили ещё одну распространённую формулировку условия, в которой предложено непосредственно вычислить двойной интеграл. Да, он численно равен площади области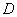 
, но, коль скоро, о площади изначально молчок, то и в решении об этом не нужно упоминать;-) Подумайте, как грамотно записать ответ задания.
Примерные образцы решений и чертежи в конце урока. Я их оформил в разном стиле, выбирайте, что больше нравится.
То были заезженные типовики, а сейчас на очереди более редкий, но очень интересный и поучительный экземпляр:
Пример 5
Вычислить двойной интеграл 
Решение: определённый интеграл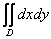 
задаёт площадь области интегрирования, но о площади нас никто не спрашивал, поэтому никого не будем загружать своей эрудицией =) К тому же она сейчас ой как потребуется для других целей.
В чём заключается особенность этого задания? Прежде всего, бросается в глаза, что область «дэ» ограничена единственной кривой, и по характерным признакам – это какая-то алгебраическая линия 4-го порядка. Основная проблема у нас с чертежом. Конечно, можно погрузиться в справочники, но на это нет ни времени, ни особого желания. Поэтому мы попытаемся ограничиться общим анализом и обойтись совсем без чертежа.