Об этом я уже говорил на 1-м уроке: если условие задачи его не требует – то можно. Правда, область интегрирования всё равно придётся представить мысленно. Но даже если у вас есть такие способности, то демонстрировать их совсем не обязательно – потому что тяжелА жизнь вундеркинда =) И житейская мудрость заключается в том, что чертёжи, по возможности лучше выполнять. Однако у нас другой случай, когда наоборот – будет подозрительно смотреться построенный график линии 4-го порядка. Знаниями убивать тоже никого не надо, и в этой связи мы постараемся отделаться чисто аналитическим решением.
Поскольку область интегрирования, как правило, ограничена, то уравнение 
задаёт либо единственную замкнутую кривую, либо несколько ограниченных областей – что-то наподобие лепестков полярной розы. Ситуацию помогла бы прояснить область определения функции, но её нахождение тоже затруднено ввиду навороченности уравнения.
Что делать? Подумать о возможности использования полярной системы координат. Причём подумать самостоятельно – условие нам совершенно не намекает на способ решения. Поскольку в уравнении присутствуют знакомые «икс квадрат» и «игрек квадрат», то применение полярных координат действительно выглядит перспективно. По формулам перехода 
:
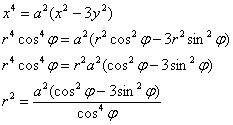
Вот и первое достижение – удалось понизить степень. С извлечением корня никаких шероховатостей, полярный радиус неотрицателен, параметр 
, косинус в знаменателе – в чётной степени:
Теперь займёмся областью определения. Поскольку тригонометрические функции периодичны, то нас интересует промежуток 
, или, что то же самое 
.
Знаменатель не может равняться нулю, поэтому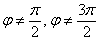 
.
Кроме того, подкоренное выражение должно быть неотрицательным: 
. Сведём данное условие к простейшему тригонометрическому неравенству, применив формулы понижения степени:
Таким образом:
Я неоднократно ратовал за графическое решение подобных неравенств, но раз уж решили обойтись без чертежей, давайте вытащим из школьного учебника известную формулу. Решением неравенства 
, где 
, является следующее множество промежутков:
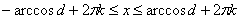, где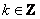 
(любое целое число).
В нашем случае:
Разделим все части неравенства на 2:
В «сферу наших интересов» входят следующие значения «ка»:
В результате, область определения полярной функции 
:
Два нижних значения не вошли в найденные выше промежутки, что избавляет нас от дополнительных хлопот. На отрезках 
расположены две одинаковые (в силу периодичности 
и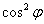 
) кривые, и график функции 
, судя по всему, представляет собой что-то вроде двух одинаковых лепестков, как, собственно, и предполагалось.
Таким образом, достаточно рассмотреть промежуток 
, а результат удвоить. Луч радара, исходя из полюса 
, сразу попадает в область интегрирования и выходит из неё через границу «лепестка»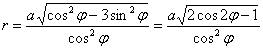 
; при этом он осуществляет поворот от значения 
до 
.
Переход к повторным интегралам, думаю, всем понятен:
1) Понеслась нелёгкая:
2) Подставляем результат предыдущего пункта во внешний интеграл, не забывая про «двойку» перед ним (удвоение «лепестка»):
На первом шаге удвоили интеграл от чётной функции по симметричному относительно нуля отрезку. Чтобы «не таскать всё за собой», подынтегральную функцию удобно преобразовать отдельно. Приведём её к пригодному (и выгодному!) для интегрирования виду:
Если где-то возникли непонятки, посмотрите тригонометрические формулы. А если появились вопросы по самим принципам решения подобных интегралов, пожалуйста, посетите уроки Интегралы от тригонометрических функций и Сложные интегралы.
Завершаем вычисления:
Ответ: 
Именно так. Не забываем, что в условии не спрашивалось о площадях и квадратных единицах. Однако после того как я нашёл в своих закромах этот трудный пример и включил его в содержание статьи, мне стало жутко интересно, так как же всё-таки выглядит график функции , и не допущена ли ошибка в вычислениях. Придав параметру значение 
, я изобразил график функции 
с помощью своего графопостроителя (см. Математические формулы и таблицы ), и полученное значение площади 
оказалось очень похоже на правду. Желающие могут проделать то же самое. А если условие подобной задачи требует чертежа – то придётся =)
Получился такой увлекательный разбор решения, что на этом фоне как-то затерялся тот момент, что в двойном интеграле 
может оказаться «настоящая» функция 
с «живым» «иксом» и/или «игреком»:
Пример 6
Вычислить двойной интеграл, используя полярные координаты
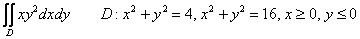
Решение: область интегрирования здесь очень простая – это часть кольца между концентрическими окружностями 
, которая располагается в четвёртой координатной четверти (о чём нам сообщают неравенства 
). И коль скоро так всё просто, можно сразу заняться переходом к полярной системе координат по формулам .
Найдём уравнения окружностей:
И выполним чертёж:
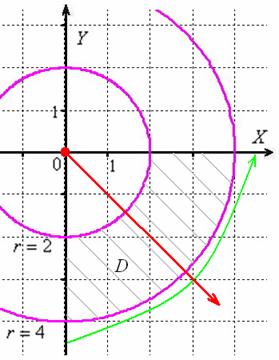
Порядок обхода области предельно понятен:
Можно было взять промежуток 
, но работать с табличным значением 
гораздо привычнее.
Отличие от предыдущих примеров состоит в дополнительном шаге – преобразовании подынтегральной функции 
. Используем те же стандартные формулы перехода . Если совсем просто, то в функцию двух переменных вместо «икс» подставляем 
и вместо «игрек» 
:
После подстановки максимально упрощаем выражение, но здесь этого особо не потребовалось.
Таким образом:
Фишка последнего шага должна быть вам хорошо знакома: когда проводится интегрирование по переменной «эр», то переменная «фи» считается константой (и наоборот). Поэтому константу 
целесообразно сразу вынести из внутреннего интеграла, чтобы она не мешалась под ногами.
Считаем:
1)
2)
Ответ: 
После того, как занавес опущен, повторим геометрический смысл полученного результата. По условию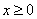 
, следовательно, 
, то есть поверхность, которую задаёт эта функция двух переменных, в 1-й и 4-й четвертях расположена над плоскостью 
. Полученный в задаче результат – это в точности объём цилиндрического бруса, который ограничен плоскостью снизу, поверхностью – сверху и множеством перпендикулярных плоскости прямых, проходящих через каждую точку границы области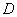 
(«четвертинки» кольца) – сбоку. Примерно 66 «кубиков»: 
С задачей нахождения объёма тела мы вплотную столкнёмся при изучении тройных интегралов.
Завершим занятие несложным примером для самостоятельного решения:
Пример 7
Вычислить двойной интеграл, используя полярные координаты
