Вариант №1
1) Прямые a и b лежат в параллельных плоскостях  и b. Могут ли эти прямые быть параллельными; скрещивающимися? Сделайте рисунок для каждого возможного случая.
и b. Могут ли эти прямые быть параллельными; скрещивающимися? Сделайте рисунок для каждого возможного случая.
2) Через точку О, лежащую между параллельными плоскостями  и
и  , проведены прямые l и m. Прямая l пересекает плоскости
, проведены прямые l и m. Прямая l пересекает плоскости  и b в точках A1 и A2 соответственно, прямая m – в точках В1 и В2. Найдите длину отрезка A2В2, если
и b в точках A1 и A2 соответственно, прямая m – в точках В1 и В2. Найдите длину отрезка A2В2, если 
3)* Дан параллелепипед АВСDA1B1C1D1. Постройте сечение параллелепипеда плоскостью, проходящей через точки М, N и К, являющиеся серединами рёбер АВ, ВС и DD1.
Вариант №2
1) Прямые a и b лежат в пересекающихся плоскостях  и b. Могут ли эти прямые быть параллельными; скрещивающимися? Сделайте рисунок для каждого возможного случая.
и b. Могут ли эти прямые быть параллельными; скрещивающимися? Сделайте рисунок для каждого возможного случая.
2) Через точку О, не лежащую между параллельными плоскостями  и
и  , проведены прямые l и m. Прямая l пересекает плоскости
, проведены прямые l и m. Прямая l пересекает плоскости  и b в точках A1 и A2 соответственно, прямая m – в точках В1 и В2. Найдите длину отрезка A1В1, если
и b в точках A1 и A2 соответственно, прямая m – в точках В1 и В2. Найдите длину отрезка A1В1, если 
3) *Дан тетраэдр DABC. Постройте сечение тетраэдра плоскостью, проходящей через точки М и N, являющиеся серединами рёбер DС и ВС, и точку К, такую, что 
КОНТРОЛЬНАЯ РАБОТА № 3 по теме «Перпендикулярность прямых и плоскостей» – 10 кл.
Вариант №1.
1) Диагональ куба равна 6см. Найдите:
а) ребро куба.
б) косинус угла между диагональю куба и плоскостью одной из его граней.
2) Сторона АВ ромба АВСD равна р, а один из углов ромба равен  . Через
. Через
сторону АВ проведена плоскость  на расстоянии р/2 от точки D.
на расстоянии р/2 от точки D.
а) Найдите расстояние от точки С до плоскости  .
.
б) Покажите на рисунке линейный угол двугранного угла DАВМ,  .
.
в)* Найдите синус угла между плоскостью ромба и плоскостью  .
.
Вариант №2.
1) Основанием прямоугольного параллелепипеда служит квадрат, диагональ параллелепипеда равна  , а его измерения относятся как 1:1:2. Найдите:
, а его измерения относятся как 1:1:2. Найдите:
а) измерения параллелепипеда.
б) синус угла между диагональю параллелепипеда и плоскостью его основания.
2) Сторона квадрата АВСD равна р. Через сторону АD проведена плоскость
 на расстоянии р/2 от точки В.
на расстоянии р/2 от точки В.
а) Найдите расстояние от точки С до плоскости  .
.
б) Покажите на рисунке линейный угол двугранного угла ВАDМ,  .
.
в)* Найдите угол между плоскостью квадрата и плоскостью  .
.
КОНТРОЛЬНАЯ РАБОТА № 4 по теме «Многогранники» – 10 кл.
Вариант №1.
1) Основанием пирамиды DАВС является правильный треугольник АВС, сторона которого равна р. Ребро DА перпендикулярно к плоскости АВС, а плоскость DВС составляет с плоскостью АВС угол  . Найдите площадь боковой и площадь полной поверхности пирамиды.
. Найдите площадь боковой и площадь полной поверхности пирамиды.
2) Основанием прямого параллелепипеда АВСDА1В1С1D1 является ромб АВСD сторона которого равна р и угол равен  . Плоскость АD1С1 составляет с плоскостью основания угол
. Плоскость АD1С1 составляет с плоскостью основания угол  . Найдите:
. Найдите:
а) высоту ромба.
б) высоту параллелепипеда.
в) площадь боковой поверхности параллелепипеда.
г)* площадь поверхности параллелепипеда.
Вариант №2.
1) Основанием пирамиды МАВСD является квадрат АВСD. Ребро МD перпендикулярно к плоскости основания, АD = DМ = р. Найдите площадь боковой и площадь полной поверхности пирамиды.
2) Основанием прямого параллелепипеда АВСDА1В1С1D1 является параллелограмм АВСD, стороны которого равна р  и 2р, острый угол равен
и 2р, острый угол равен  . Высота параллелепипеда равна меньшей высоте параллелограмма. Найдите:
. Высота параллелепипеда равна меньшей высоте параллелограмма. Найдите:
а) меньшую высоту параллелограмма.
б) угол между плоскостью АВС1 и плоскостью основания.
в) площадь боковой поверхности параллелепипеда.
г)* площадь поверхности параллелепипеда.
КОНТРОЛЬНАЯ РАБОТА № 5 по теме «Простейшие задачи в координатах» (20мин)– 11 класс
Вариант №1.
1) Найдите координаты вектора  , если А(5; -1; 3), В(2; -2; 4).
, если А(5; -1; 3), В(2; -2; 4).
2) Даны векторы  {3; 1; -2},
{3; 1; -2},  {1; 4; -3}. Найдите |
{1; 4; -3}. Найдите |  -
-  .
.
3) Изобразите систему координат Оxyz и постройте точку А(1; -2; -4). Найдите расстояние от этой точки до координатных плоскостей.
Вариант №2
1) Найдите координаты вектора  ,, если А(6; 3; -2), В(2; 4; -5).
,, если А(6; 3; -2), В(2; 4; -5).
2) Даны векторы  {5; -1; 2},
{5; -1; 2},  {3; 2; -4}. Найдите |
{3; 2; -4}. Найдите |  -
-  .
.
3) Изобразите систему координат Оxyz и постройте точку В(-2; -3; 4).
Найдите расстояние от этой точки до координатных плоскостей.
КОНТРОЛЬНАЯ РАБОТА № 6 по теме «Метод координат в пространстве» – 11 класс
Вариант №1.
1) Дан куб АВСDА1В1С1D1. Найдите угол между прямыми АD1 и ВМ, где М – середина ребра DD1.
2) Вычислите скалярное произведение векторов  и
и  , если
, если
 ,
,  =
=  , |
, |  | =2,
| =2, 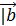 | =3, (
| =3, ( ,
,  ^
^  ^
^ 
3) При движении прямая а отображается на прямую 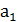 , а плоскость a - на плоскость
, а плоскость a - на плоскость 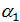 . Докажите, что если а || a, то
. Докажите, что если а || a, то 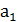 ||
|| 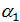 .
.
Вариант №2
1) Дан куб АВСDА1В1С1D1. Найдите угол между прямыми АС и DС1.
2) Вычислите скалярное произведение векторов  и
и 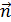 , если
, если
 ,
,  =
=  , |
, |  | =3,
| =3, 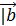 | =2, (
| =2, ( ,
,  ^
^  ^
^ 
3) При движении прямая а отображается на прямую 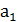 , а плоскость a - на плоскость
, а плоскость a - на плоскость 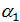 . Докажите, что если а ^ a, то
. Докажите, что если а ^ a, то 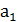 ^
^ 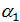 .
.
КОНТРОЛЬНАЯ РАБОТА № 7 по теме «Тела вращения» – 11кл
Вариант №1.
1) Осевое сечение цилиндра – квадрат. Площадь основания цилиндра равна  . Найдите площадь полной поверхности цилиндра.
. Найдите площадь полной поверхности цилиндра.
2) Высота конуса равна 6см. Угол при вершине осевого сечения равен  .
.
а) Найти площадь сечения конуса плоскостью, проходящей через две образующие, угол между которыми равен  .
.
б) Найти площадь боковой поверхности конуса.
3) Диаметр шара равен 2р. Через конец диаметра проведена плоскость под углом  к нему. Найдите длину линии пересечения сферы этой плоскостью.
к нему. Найдите длину линии пересечения сферы этой плоскостью.
Вариант №2
1) Осевое сечение цилиндра – квадрат, диагональ которого равна 4см. Найдите площадь полной поверхности цилиндра.
2) Радиус основания конуса равен 6см, а образующая наклонена к плоскости основания под углом  .
.
а) Найти площадь сечения конуса плоскостью, проходящей через две образующие, угол между которыми равен  .
.
б) Найти площадь боковой поверхности конуса.
3) Диаметр шара равен 4р. Через конец диаметра проведена плоскость под углом  к нему. Найдите площадь сечения шара этой плоскостью.
к нему. Найдите площадь сечения шара этой плоскостью.
КОНТРОЛЬНАЯ РАБОТА №8 по теме «Объёмы тел» – 11 класс
Вариант №1.
1) Диаметр шара равен высоте конуса, образующая которого составляет с плоскостью основания угол  . Найдите отношение объёмов конуса и шара.
. Найдите отношение объёмов конуса и шара.
2) Объём цилиндра равен  , площадь его осевого сечения
, площадь его осевого сечения  . Найдите площадь сферы, описанной около цилиндра.
. Найдите площадь сферы, описанной около цилиндра.
Вариант №2.
1) В конус, осевое сечение которого есть правильный треугольник, вписан шар. Найдите отношение площади сферы к площади боковой поверхности конуса.
2) Диаметр шара равен высоте цилиндра, осевое сечение которого есть квадрат. Найдите отношение объёмов шара и цилиндра.