Задание 2. Вычислить определённые интегралы:
2.1.  .
.
Решение.  .
.
2.2. 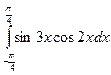 .
.
Решение. 
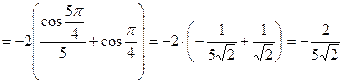 .
.
2.3.  .
.
Решение.  .
.
Задание 3. Вычислить несобственный интеграл или доказать, что он расходится:
 .
.
Решение. Точка  является особой точкой, поскольку подынтегральная функция имеет в ней бесконечный разрыв. Поэтому:
является особой точкой, поскольку подынтегральная функция имеет в ней бесконечный разрыв. Поэтому:
 - получили бесконечный предел.
- получили бесконечный предел.
Таким образом, данный интеграл расходится.
Задание 4. Найти площадь фигуры, ограниченной линиями:
 .
.
Решение. Площадь данной фигуры равна разности площадей криволинейных трапеций, образованных прямой  и гиперболой
и гиперболой  на отрезке
на отрезке  .
.
 .
.
Задание 5. Вычислить объём тела, полученного при вращении вокруг оси абсцисс фигуры, ограниченной линиями:
 .
.
Решение. Используем формулу для нахождения объёма тел вращения:  .
.
 .
.
Вариант № 1.
Задание 1. Найти неопределённые интегралы:
1.1.  ; 1.2.
; 1.2.  ; 1.3.
; 1.3.  ; 1.4.
; 1.4.  ; 1.5.
; 1.5.  ;
;
1.6.  ; 1.7.
; 1.7.  ; 1.8.
; 1.8. 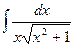 ; 1.9.
; 1.9.  ; 1.10.
; 1.10.  .
.
Задание 2. Вычислить определённые интегралы:
2.1.  ; 2.2.
; 2.2. 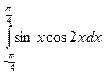 ; 2.3.
; 2.3.  .
.
Задание 3. Вычислить несобственный интеграл или доказать, что он расходится:
 .
.
Задание 4. Найти площадь фигуры, ограниченной линиями:
 .
.
Задание 5. Вычислить объём тела, полученного при вращении вокруг оси абсцисс фигуры, ограниченной линиями:
 .
.
Вариант № 2.
Задание 1. Найти неопределённые интегралы:
1.1.  ; 1.2.
; 1.2.  ; 1.3.
; 1.3.  ; 1.4.
; 1.4. 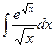 ; 1.5.
; 1.5.  ;
;
1.6.  ; 1.7.
; 1.7.  ; 1.8.
; 1.8.  ; 1.9.
; 1.9.  ; 1.10.
; 1.10.  .
.
Задание 2. Вычислить определённые интегралы:
2.1.  ; 2.2.
; 2.2. 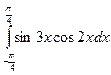 ; 2.3.
; 2.3. 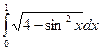 .
.
Задание 3. Вычислить несобственный интеграл или доказать, что он расходится:
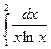 .
.
Задание 4. Найти площадь фигуры, ограниченной линиями:
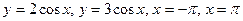 .
.
Задание 5. Вычислить объём тела, полученного при вращении вокруг оси абсцисс фигуры, ограниченной линиями:
 .
.
Вариант № 3.
Задание 1. Найти неопределённые интегралы:
1.1.  ; 1.2.
; 1.2. 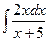 ; 1.3.
; 1.3.  ; 1.4.
; 1.4.  ; 1.5.
; 1.5.  ;
;
1.6.  ; 1.7.
; 1.7.  ; 1.8.
; 1.8. 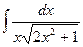 ; 1.9.
; 1.9.  ; 1.10.
; 1.10.  .
.
Задание 2. Вычислить определённые интегралы:
2.1.  ; 2.2.
; 2.2.  ; 2.3.
; 2.3.  .
.
Задание 3. Вычислить несобственный интеграл или доказать, что он расходится:
 .
.
Задание 4. Найти площадь фигуры, ограниченной линиями:
 .
.
Задание 5. Вычислить объём тела, полученного при вращении вокруг оси абсцисс фигуры, ограниченной линиями:
 .
.
Вариант № 4.
Задание 1. Найти неопределённые интегралы:
1.1.  ; 1.2.
; 1.2.  ; 1.3.
; 1.3.  ; 1.4.
; 1.4. 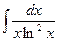 ; 1.5.
; 1.5. 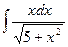 ;
;
1.6.  ; 1.7.
; 1.7.  ; 1.8.
; 1.8.  ; 1.9.
; 1.9.  ; 1.10.
; 1.10.  .
.
Задание 2. Вычислить определённые интегралы:
2.1.  ; 2.2.
; 2.2.  ; 2.3.
; 2.3.  .
.
Задание 3. Вычислить несобственный интеграл или доказать, что он расходится:
 .
.
Задание 4. Найти площадь фигуры, ограниченной линиями:
 .
.
Задание 5. Вычислить объём тела, полученного при вращении вокруг оси абсцисс фигуры, ограниченной линиями:
 .
.
Вариант № 5.
Задание 1. Найти неопределённые интегралы:
1.1.  ; 1.2.
; 1.2.  ; 1.3.
; 1.3.  ; 1.4.
; 1.4.  ; 1.5.
; 1.5.  ;
;
1.6.  ; 1.7.
; 1.7.  ; 1.8.
; 1.8.  ; 1.9.
; 1.9. 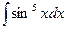 ; 1.10.
; 1.10.  .
.
Задание 2. Вычислить определённые интегралы:
2.1.  ; 2.2.
; 2.2. 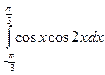 ; 2.3.
; 2.3.  .
.
Задание 3. Вычислить несобственный интеграл или доказать, что он расходится:
 .
.
Задание 4. Найти площадь фигуры, ограниченной линиями:
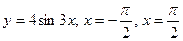 .
.
Задание 5. Вычислить объём тела, полученного при вращении вокруг оси абсцисс фигуры, ограниченной линиями:
 .
.
Вариант № 6.
Задание 1. Найти неопределённые интегралы:
1.1.  ; 1.2.
; 1.2. 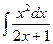 ; 1.3.
; 1.3. 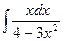 ; 1.4.
; 1.4. 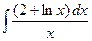 ; 1.5.
; 1.5.  ;
;
1.6.  ; 1.7.
; 1.7.  ; 1.8.
; 1.8.  ; 1.9.
; 1.9.  ; 1.10.
; 1.10.  .
.
Задание 2. Вычислить определённые интегралы:
2.1.  ; 2.2.
; 2.2.  ; 2.3.
; 2.3.  .
.
Задание 3. Вычислить несобственный интеграл или доказать, что он расходится:
 .
.
Задание 4. Найти площадь фигуры, ограниченной линиями:
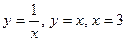 .
.
Задание 5. Вычислить объём тела, полученного при вращении вокруг оси абсцисс фигуры, ограниченной линиями:
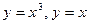 .
.
Вариант № 7.
Задание 1. Найти неопределённые интегралы:
1.1.  ; 1.2.
; 1.2.  ; 1.3.
; 1.3.  ; 1.4.
; 1.4.  ; 1.5.
; 1.5.  ;
;
1.6.  ; 1.7.
; 1.7.  ; 1.8.
; 1.8.  ; 1.9.
; 1.9.  ; 1.10.
; 1.10.  .
.
Задание 2. Вычислить определённые интегралы:
2.1.  ; 2.2.
; 2.2.  ; 2.3.
; 2.3.  .
.
Задание 3. Вычислить несобственный интеграл или доказать, что он расходится:
 .
.
Задание 4. Найти площадь фигуры, ограниченной линиями:
 .
.
Задание 5. Вычислить объём тела, полученного при вращении вокруг оси абсцисс фигуры, ограниченной линиями:
 .
.
Вариант № 8.
Задание 1. Найти неопределённые интегралы:
1.1.  ; 1.2.
; 1.2.  ; 1.3.
; 1.3.  ; 1.4.
; 1.4.  ; 1.5.
; 1.5.  ;
;
1.6.  ; 1.7.
; 1.7.  ; 1.8.
; 1.8.  ; 1.9.
; 1.9.  ; 1.10.
; 1.10.  .
.
Задание 2. Вычислить определённые интегралы:
2.1.  ; 2.2.
; 2.2.  ; 2.3.
; 2.3.  .
.
Задание 3. Вычислить несобственный интеграл или доказать, что он расходится:
 .
.
Задание 4. Найти площадь фигуры, ограниченной линиями:
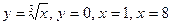 .
.
Задание 5. Вычислить объём тела, полученного при вращении вокруг оси ординат фигуры, ограниченной линиями:
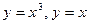 .
.
Вариант № 9.
Задание 1. Найти неопределённые интегралы:
1.1.  ; 1.2.
; 1.2.  ; 1.3.
; 1.3.  ; 1.4.
; 1.4.  ; 1.5.
; 1.5.  ;
;
1.6.  ; 1.7.
; 1.7.  ; 1.8.
; 1.8.  ; 1.9.
; 1.9.  ; 1.10.
; 1.10.  .
.
Задание 2. Вычислить определённые интегралы:
2.1.  ; 2.2.
; 2.2.  ; 2.3.
; 2.3. 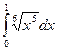 .
.
Задание 3. Вычислить несобственный интеграл или доказать, что он расходится:
 .
.
Задание 4. Найти площадь фигуры, ограниченной линиями:
 .
.
Задание 5. Вычислить объём тела, полученного при вращении вокруг оси ординат фигуры, ограниченной линиями:
 .
.
Вариант № 10.
Задание 1. Найти неопределённые интегралы:
1.1.  ; 1.2.
; 1.2.  ; 1.3.
; 1.3.  ; 1.4.
; 1.4.  ; 1.5.
; 1.5. 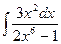 ;
;
1.6.  ; 1.7.
; 1.7.  ; 1.8.
; 1.8.  ; 1.9.
; 1.9. 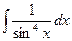 ; 1.10.
; 1.10.  .
.
Задание 2. Вычислить определённые интегралы:
2.1.  ; 2.2.
; 2.2.  ; 2.3.
; 2.3.  .
.
Задание 3. Вычислить несобственный интеграл или доказать, что он расходится:
 .
.
Задание 4. Найти площадь фигуры, ограниченной линиями:
 .
.
Задание 5. Вычислить объём тела, полученного при вращении вокруг оси ординат фигуры, ограниченной линиями:
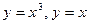 .
.
Вариант № 11.
Задание 1. Найти неопределённые интегралы:
1.1.  ; 1.2.
; 1.2.  ; 1.3.
; 1.3.  ; 1.4.
; 1.4.  ; 1.5.
; 1.5.  ;
;
1.6.  ; 1.7.
; 1.7. 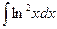 ; 1.8.
; 1.8.  ; 1.9.
; 1.9. 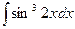 ; 1.10.
; 1.10.  .
.
Задание 2. Вычислить определённые интегралы:
2.1.  ; 2.2.
; 2.2.  ; 2.3.
; 2.3.  .
.
Задание 3. Вычислить несобственный интеграл или доказать, что он расходится:
 .
.
Задание 4. Найти площадь фигуры, ограниченной линиями:
 .
.
Задание 5. Вычислить объём тела, полученного при вращении вокруг оси абсцисс фигуры, ограниченной линиями:
 .
.
Вариант № 12.
Задание 1. Найти неопределённые интегралы:
1.1.  ; 1.2.
; 1.2.  ; 1.3.
; 1.3.  ; 1.4.
; 1.4.  ; 1.5.
; 1.5.  ;
;
1.6.  ; 1.7.
; 1.7.  ; 1.8.
; 1.8. 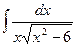 ; 1.9.
; 1.9.  ; 1.10.
; 1.10. 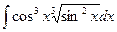 .
.
Задание 2. Вычислить определённые интегралы:
2.1.  ; 2.2.
; 2.2.  ; 2.3.
; 2.3.  .
.
Задание 3. Вычислить несобственный интеграл или доказать, что он расходится:
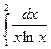 .
.
Задание 4. Найти площадь фигуры, ограниченной линиями:
 .
.
Задание 5. Вычислить объём тела, полученного при вращении вокруг оси абсцисс фигуры, ограниченной линиями:
 .
.