ПРОГРАММА
по учебной дисциплине «Математика»
на 2 семестр 2012/2013 учебный год
для курсантов 1 курса очной формы обучения
(специальность: 090915 – безопасность информационных технологий в правоохранительной деятельности)
Факультет: ФПСОИБ
Раздел 2. Элементы линейной алгебры и аналитической геометрии
Тема 9. Матрицы и определители
1. Матрицы: понятие, обозначения, отдельные частные виды матриц.
2. Основные операции над матрицами и их свойства.
3. Элементарные преобразования матриц, эквивалентные матрицы.
4. Ступенчатый вид матрицы. Приведение матрицы к ступенчатому виду.
5. Подстановки: понятие, обозначения, степень и четность подстановки, мощность 
.
6. Понятие определителя матрицы.
7. Свойства определителей матриц.
8. Подматрица, минор, дополнительный минор, алгебраическое дополнение: понятия и обозначения.
9. Теорема Лапласа (общая формулировка).
10. Следствие из теоремы Лапласа для случая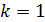 
(разложение определителя по строке или столбцу).
11. Изменение определителя матрицы при элементарных преобразованиях.
12. Обратная матрица: понятие, обозначение, теорема об обратной матрице.
13. Нахождение обратной матрицы с помощью элементарных преобразований.
Тема 10. Векторные (линейные) пространства
14. Понятие бинарной операции на произвольном множестве.
15. Понятие векторного (линейного) пространства над произвольным полем. Примеры векторных пространств.
16. Линейная зависимость и независимость векторов, основная лемма о линейной зависимости.
17. База системы векторов и ее свойства.
18. Ранг матрицы, теорема о ранге матрицы, вычисления ранга матрицы с помощью элементарных преобразований.
19. Критерий равенства определителя нулю.
20. Базис и размерность векторного пространства.
21. Размерность арифметического векторного пространства 
.
22. Подпространство векторного пространства. Линейная оболочка системы векторов.
23. Координаты вектора в конечномерном пространстве. Изменение координат вектора при переходе между базисами.
24. Определение линейной зависимости или независимости векторов в произвольном конечномерном пространстве с помощью понятия ранга матрицы.
25. Линейный оператор, матричное задание линейного оператора, понятие изоморфизма линейных пространств, изоморфизм линейных пространств одинаковой размерности.
26. Образ и ядро линейного оператора, размерность образа и ядра, критерий инъективности линейного оператора.
Тема 11. Системы линейных уравнений
27. Понятие и виды систем линейных уравнение, понятие решения системы линейных уравнений, матричная форма записи системы линейных уравнений и её решения.
28. Совместность, несовместность, определенность, неопределенность систем линейных уравнений, теорема Кронеккера-Капелли.
29. Методы решения совместных определенных систем линейных уравнений, их суть и ограничения в применении.
30. Решение совместных неопределенных систем линейных уравнений: структура решения и нахождение его составляющих элементов.
31. Определение несовместности системы линейных уравнений.
Тема 12. Векторная алгебра
32. Геометрическое понятие вектора, равные векторы, операции над векторами.
33. Векторные пространства 
и их размерности.
34. Системы координат на плоскости: аффинная (декартова), полярная.
35. Системы координат в пространстве: аффинная (декартова), цилиндрическая, сферическая.
36. Координатная запись операций над векторами.
37. Понятие скалярного произведения, его свойства и выражение через координаты.
38. Понятие векторного произведения, его свойства и выражение через координаты.
39. Смешанное произведение, его свойства и выражение через координаты.
Тема 13. Прямая и плоскость
40. Уравнения прямой, взаимное расположение прямых, угол между прямыми, расстояние от точки до прямой на плоскости.
41. Уравнения прямой, взаимное расположение прямых, угол между прямыми, расстояние от точки до прямой в пространстве, расстояние между скрещивающимися прямыми.
42. Уравнения плоскости, взаимное расположение плоскостей, угол между плоскостями, расстояние между параллельными плоскостями.
Тема 14. Кривые второго порядка
43. Понятие кривой второго порядка, теорема о каноническом виде уравнения кривой второго порядка.
44. Преобразование координат, приведение к каноническому виду общего уравнения кривой второго порядка.
45. Задача, приводящая к понятиям параболы, эллипса, гиперболы. Понятие директрисы, фокуса, эксцентриситета.
46. Уравнение, график, малая и большая полуоси, фокусы, директрисы, эксцентриситет, прямоугольник, фокальное свойство эллипса. Случай окружности.
47. Уравнение, график, фокусы, директрисы, эксцентриситет, прямоугольник, фокальное свойство гиперболы.
48. Уравнение, график, фокус, параметр, директриса, эксцентриситет параболы.