Алгоритм выполнения заданий

Задание

1. Изучить использование критерия j^* – угловое преобразование Фишера

2. Следуя алгоритму решить 2 задания, используя критерий j^* – угловое преобразование Фишера, сформулируйте гипотезы и напишите выводы.

3. Задание 1 представлено как ПРИМЕР РЕШЕНИЯ!

4. На стр 8 данного документа представлено «Домашнее занятие». Решить представленные 4 задания по указанному в Практическом занятии алгоритму используя критерия j^* – угловое преобразование Фишера.

5. Предварительно оцените возможность использование j^* – угловое преобразование Фишера в решении 4х заданий. Ответ обоснуйте.

Практическое занятие

Цель задания. Оценка достоверности различия в значениях исследуемых признаков

Аппаратура. Персональный компьютер.

Математическое обеспечение. Операционная система WINDOWS-95 и пакет EXCEL 7.0.

Теоретическое обеспечение.

1. Статистические гипотезы

2. Критерий j^* – угловое преобразование Фишера.

3. Интерпретация результатов

Алгоритм выполнения заданий

1. Сформулировать гипотезы ( в тетради )

2. Решить задание ( в таблице EXCEL )

3. Написать вывод (заключение) ( в тетради )

Критерий j^* – угловое преобразование Фишера оценивает достоверность различий между процентными долями двух выборок, в которых зарегистрирован интересующий исследователя эффект. Сущность его состоит в переводе процентных долей в величины центрального угла, измеряемого в радианах: j = arcsin Р, где P – процентная доля, выраженная в долях единицы. При увеличении расхождения между углами j₁ и j₂ и увеличении объема выборок значение критерия возрастает, и чем больше величина j^*, тем более вероятно, что различия достоверны.

Гипотезы:

Н₀: Доля лиц, у которых проявляется исследуемый эффект, в выборке 1, не больше, чем в выборке 2.

Н₁: Доля лиц, у которых проявляется исследуемый эффект, в выборке 1, больше, чем в выборке 2.

АЛГОРИТМ Расчета критерия j^*.

1. Определить те значения признака, которые будут разделять испытуемых на тех, у кого «есть эффект» и тех, у кого «нет эффекта». Если признак измерен количественно, можно использовать критерий l для поиска оптимальной точки разделения.

2. Начертить четырехклеточную таблицу из двух столбцов и двух строк. Первый столбец – «есть эффект», второй – «нет эффекта», первая строка сверху – 1 группа (выборка), вторая строка – 2 группа (выборка).

3. Подсчитать количество испытуемых в первой группе, у которых «есть эффект», и занести это число в левую верхнюю ячейку таблицы.

4. Подсчитать количество испытуемых в первой группе, у которых «нет эффекта», и занести это число в правую верхнюю ячейку таблицы. Сумма по двум верхним ячейкам должна совпадать с числом испытуемых в первой группе.

5. Подсчитать количество испытуемых во второй группе, у которых «есть эффект», и занести это число в левую нижнюю ячейку таблицы.

6. Подсчитать количество испытуемых во второй выборке, у которых «нет эффекта», и занести это число в правую нижнюю ячейку таблицы. Сумма по двум нижним ячейкам должна совпадать с числом испытуемых во второй группе.

7. Определить процентные доли испытуемых, у которых «есть эффект», деля их количество на общее число испытуемых в данной группе и умножая на 100%. Записать их в скобках на соответствующих полях таблицы.

8. Проверить, не равняется ли одна из долей нулю. Если так, попробовать изменить это, сдвинув точку разделения групп в какую-либо сторону. Если это невозможно, использовать для решения критерий c².

9. Определить по таблице величины углов j ₁ и j ₂. Вычислить эмпирическое значение критерия j^* по формуле:

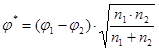где: j₁– угол, соответствующий большей процентной доле,

j₂ – угол, соответствующий меньшей процентной доле,

n ₁ – объем выборки 1, n ₂ – объем выборки 2.

10. Сравнить полученное значение j^* с критическими значениями: j^*_кр= 1,64 для a = 0,05 и j^*_кр= 2,31 для a = 0,01.Если j^*_эмп>j^*_кр, то Н₀ отвергается.

При необходимости определить точный уровень значимости полученного j^*_эмп по соответствующей таблице.

Задание 1. ПРИМЕР РЕШЕНИЯ Сопоставление выборок по качественно определяемому признаку. Две группыстудентов решали новую экспериментальную задачу. В первой группе из 20 человек с задачей справились 12 человек, а во второй группе из 25 человек – 10. Различаются ли группы по успешности решения задачи?

В первой выборке процентная доля решивших задачу студентов составила 12/20×100% = 60%, а во второй – 10/25×100% = 40%. Достоверны ли эти различия при данных n₁и n₂?

Поскольку нас интересует факт решения задачи, будем считать, что «эффект есть», если задача решена. Сформулируем гипотезы.

Н₀: Доля лиц, решивших задачу, в первой группе не больше, чем во второй группе.

Н₁: Доля лиц, решивших задачу, в первой группе больше, чем во второй группе.

В соответствии с алгоритмом 14 построим четырехклеточную (четырехпольную) таблицу 5.1.

Таблица 5.1

Расчет критерия при сопоставлении двух групп испытуемых по процентной доле решивших задачу.

Группы	«Есть эффект»	«Нет эффекта»	Суммы
Количество испытуемых	% доля	Количество испытуемых	% доля
1 группа		(60%)		(40%)
2 группа		(40%)		(60%)
Суммы

По таблице определяем величины j₁ и j₂: j₁(60%) = 1,772; j₂(40%) = 1,369. Вычислим эмпирическое значение критерия:

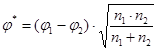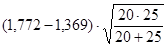= =0,403× 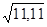= 1,34.

По таблице определяем, что это значение соответствует уровню значимости a = 0,09.

Вывод. Гипотеза Н₀ принимается. Доля студентов, решивших задачу, в первой группе не больше, чем во второй.

Задание 2. Сопоставление выборок по количественно определяемому признаку. Из 70 юношей – учащихся ПТУ по опроснику были отобраны 10 испытуемых с высоким показателем по шкале «агрессивность» и 11 – с низким показателем по этой шкале. Надо определить, различаются ли группы агрессивных и неагрессивных юношей по показателю расстояния, которое они спонтанно выбирают в разговоре с сокурсником (исследование Г.А. Тлегеновой, [3]). Данные представлены в таблице.

Таблица

Показатели расстояния, выбираемого агрессивными и неагрессивными юношами в разговоре с сокурсником.

Группа 1 – высокая агрессивность	Группа 2 – низкая агрессивность
№ испытуемого	Расстояние d (см)	№ испытуемого	Расстояние d (см)

Задание 3. Сопоставление выборок и по уровню, и по распределению признака. В исследовании Р. Т. Чиркиной (1995) впервые использовался опросник, направленный на выявление тенденции к вытеснению из памяти фактов, имен, намерений и способов действия, обусловленному личными, семейными и профессиональными комплексами [3]. Выборка из 50 студентов была обследована с помощью этого опросника, а также методики Менестера – Корзини для выявления интенсивности ощущения собственной недостаточности, или «комплекса неполноценности». Результаты представлены в таблице.

Таблица

Показатели интенсивности ощущения собственной недостаточности в группах студентов с высокой (n₁=18) и низкой (n₂=24) энергией вытеснения.

Группа 1: энергия вытеснения от 19 до 31 балла (n₁=18)	Группа 2: энергия вытеснения от 7 до 13 баллов (n₁=18)
0; 0; 0; 0; 0 20; 20 30; 30; 30; 30; 30; 30 50; 50 60; 60	0;0 5; 5; 5; 5 10; 10; 10; 10;10;10 15; 15 20; 20; 20; 20 30; 30; 30; 30; 30; 30
Суммы
Средние	26,11	15,42

Вопрос Можно ли утверждать, что между показателем энергии вытеснения, диагностируемым с помощью опросника, и показателем интенсивности ощущения собственной недостаточности существуют какие-либо значимые соотношения?

Приложение 1

Величины угла φ (в радианах) для разных процентных долей: φ=2arcsin√P (по Урбаху В.Ю., 1964)

%доля				%, последний десятичный знак
			з
			Значения φ=2 arcsin√P
0,0	0,000	0,020	0,028	0,035	0,040	0,045	0,049	0,053	0,057	0,060
0,1	0,063	0,066	0,069	0,072	0,075	0,077	0,080	0,082	0,085	0,087
0,2	0,089	0,092	0,094	0 096	0.098	0,100	0,102	0,104	0,106	0,108
0.3	0,110	0,111	0,113	0,115	0,117	0,118	0,120	0,122	0,123	0,125
0,4	0,127	0,128	0,130	0,131	0,133	0,134	0,136	0,137	0,139	0,140
0,5	0,142	0,143	0.144	0,146	0,147	0,148	0,150	0,151	0,153	0,154
0,6	0,155	0,156	0,158	0,159	0,160	0,161	0,163	0,164	0,165	0,166
0,7	0,168	0,169	0,170	0,171	0,172	0,173	0,175	0,176	0,177	0,178
0,8	0,179	0,180	0,182	0,183	0,184	0,185	0,186	0,187	0,188	0,189
0,9	0,190	0,191	0,192	0,193	0,194	0,195	0,196	0,197	0,198	0,199
	0,200	0,210	0,220	0,229	0,237	0,246	0,254	0,262	0,269	0,277
	0,284	0,291	0,298	0,304	0,311	0,318	0,324	0,330	0.336	0,342
	0,348	0,354	0,360	0,365	0,371	0,376	0,382	0,387	0,392	0,398
	0,403	0,408	0,413	0,418	0,423	0,428	0,432	0,437	0,442	0,446
	0,451	0,456	0,460	0,465	0,469	0,473	0,478	0,482	0.486	0,491
	0,495	0,499	0,503	0,507	0,512	0,516	0,520	0,524	0,528	0,532
	0,536	0,539	0,543	0,547	0,551	0,555	0,559	0,562	0,566	0,570
	0,574	0,577	0,581	0,584	0,588	0,592	0,595	0,599	0,602	0,606
	0,609	0,613	0,616	0,620	0,623	0,627	0,630	0.633	0,637	0,640
	0,644	0,647	0,650	0,653	0,657	0,660	0,663	0,666	0,670	0,673
	0,676	0,679	0,682	0,686	0,689	0,692	0,695	0,698	0,701	0,704
	0,707	0,711	0,714	0,717	0,720	0,723	0,726	0,729	0,732	0,735
	0,738	0,741	0,744	0,747	0,750	0,752	0,755	0,758	0,761	0,764
	0,767	0,770	0,773	0,776	0,778	0,781	0,784	0.787	0,790	0.793
	0,795	0,798	0,801	0,804	0,807	0,809	0,812	0,815	0,818	0,820
	0,823	0,826	0,828	0,831	0,834	0,837	0,839	0,842	0,845	.0,847
	0,850	0,853	0,855	0,858	0.861	0.863	0,866	0,868	0,871	0,874
	0,876	0,879	0,881	0,884	0.887	0,889	0,892	0,894	0,897	0,900
	0,902	0,905	0,907	0,910	0,912	0.915	0,917	0,920	0,922	0,925
	0,927	0,930	0,932	0,935	0,937	0,940	0,942	0,945	0,947	0,950
	0,952	0,955	0,957	0,959	0,962	0,964	0,967	0,969	0,972	0,974
	0.976	0,979	0,981	0,984	0,986	0,988	0,991	0,993	0,996	0,998
	1,000	1.003	1,005	1,007	1,010	1,012	1,015	1.017	1,019	1,022
	1.024	1,026	1,029	1.031	1,033	1.036	1,038	1,040	1,043	1,045
	1,047	1,050	1.052	1,054	1,056	1,059	1,061	1,063	1,066	1,068
		1,072	1,075	1,077	1,079	1,082	1,084	1,086	1,088	1,091
	1,093		1,097	1,100	1,102	1,104	1,106	1.109	1,111	1,113
	1,115	1,117	1,120	1,122	1,124	1,126	1,129	1,131	1,133	1,135
	1,137	1,140	1,142	1,144	1,146	1,148	1,151	1,153	1,155	1,157
	1,159	1.161	1,164	1,166	1,168	1,170	1,172	1,174	1,177	1,179
	1,182	1,183	1,185	1,187	1,190	1,192	1,194	1,196	1,198	1,200
	1,203	1,205	1.207	1,209	1,211	1,213	1,215	1,217	1,220	1,222
	1,224	1,226	1,228	1,230	1,232	1,234	1,237	1,239	1,241	1,243
	1,245	1,247	1,249	1,251	1,254	1,256	1,258	1,260	1,262	1,264
	1,266	1.268	1,270	1,272	1.274	1,277	1,279	1,281	1,283	1,285
	1,287	1,289	1,291	1,293	1,295	1,297	1,299	1,302	1,304	1,306
	1,308	1,310	1,312	1,314	1,316	1,318	1,320	1,322	1,324	1,326
	1,328	1,330	1,333	1,335	1,337	1,339	1,341	1,343	1,345	1,347
	1,349	1,351	1,353	1,355	1,357	1,359	1,361	1,363	1,365	1,367
	1,369	1,371	1,374	1,376	1,378	1,380	1,382	1,384	1,386	1,388
	1,390	1,392	1,394	1,396	1,398	1,400	1,402	1,404	1,406	1,408
	1,410	1,412	1,414	1,416	1.418	1,420	1,422	1,424	1,426	1,428
	1,430	1,432	1,434	1,436	1,438	1,440	1,442	1,444	1,446	1,448
	1,451	1,453	1,455	1,457	1,459	1,461	1,463	1,465	1,467	1,469
	1,471	1,473	1,475	1,477	1,479	1,481	1,483	1,485	1,487	1,489
	1,491	1.493	1,495	1,497	1,499	1,501	1,503	1,505	1,507	1,509
	1,511	1,513	1,515	1,517	1,519	1,521	1,523	1,525	1,527	1,529
	1,531	1,533	1.535	1,537	1,539	1,541	1,543	1,545	1.547	1,549
	1,551	1,553	1,555	1,557	1,559	1,561	1,563	1,565	1.567	1,569
	1,571	1,573	1,575	1,577	1,579	1,581	1,583	1,585	1,587	1,589
	1,591	1,593	1,595	1,597	1,599	1,601	1,603	1,605	1,607	1,609
	1,611	1,613	1,615	1,617	1,619	1,621	1,623	1,625	1,627	1,629
	1,631	1,633	1,635	1,637	1,639	1,641	1,643	1,645	1,647	1,649
	1,651	1,653	1,655	1,657	1,659	1,661	1,663	1,665	1,667	1,669
	1.671	1,673	1,675	1,677	1,679	1,681	1,683	1,685	1,687	1,689
	1,691	1,693	1,695	1,697	1,699	1,701	1,703	1,705	1,707	1,709
	1,711	1,713	1,715	1,717	1,719	1,721	1,723	1,725	1.727	1,729
	1,731	1.734	1,736	1,738	1,740	1,742	1,744	1,746	1.748	1,750
	1,752	1,754	1,756	1,758	1,760	1,762	1,764	1,766	1.768	1,770
	1,772	1,774	1,776	1,778	1,780	1,782	1,784	1,786	1,789	1,791
	1,793	1,795	1,797	1,799	1,801	1,803	1,805	1,807	1,809	1,811
	1,813	1,815	1,817	1,819	1,821	1,823	1,826	1,828	1,830	1,832
	1,834	1,836	1,838	1,840	1,842	1,844	1,846	1,848	1,850	1,853
	1,855	1,857	1,859	1,861	1.863	1,865	1,867	1,869	1.871	1,873
	1.875	1,878	1,880	1,882	1,884	1,886	1,888	1,890	1.892	1,894
	1,897	1,899	1,901	1,903	1,905	1,907	1,909	1,911	1.913	1,916
	1,918	1,920	1,922	1,924	1,926	1,928	1,930	1,933	1.935	1,937
	1,939	1.941	1,943	1,946	1,948	1,950	1,952	1,954	1,956	1,958
	1,961	1,963	1,965	1,967	1.969	1,971	1,974	1,976	1,978	1,980
	1,982	1,984	1,987	1,989	1,991	1,993	1,995	1,998	2,000	2,002
	2.004	2,006	2,009	2,011	2.013	2,015	2,018	2,020	2,022	2.024
	2,026	2,029	2,031	2,033	2,035	2,038	2,040	2,042	2,044	2,047
	2,049	2,051	2,053	2,056	2,058	2,060	2,062	2,065	2,067	2,069
	2,071	2,074	2,076	2,078	2,081	2,083	2,085	2,087	2,090	2,092
	2,094	2,097	2,099	2,101	2,104	2,106	2,108	2,111	2,113	2.115
	2,118	2,120	2,122	2,125	2,127	2,129	2,132	2.134	2,136	2,139
	2,141	2,144	2,146	2.148	2,151	2,153	2,156	2,158	2,160	2,163
	2,165	2,168	2,170	2,172	2,175	2,177	2.180	2.182	2,185	2,187
	2,190	2,192	2,194	2.197	2,199	2,202	2,204	2,207	2,209	2,212
	2,214	2,217	2,219	2,222	2,224	2,227	2,229	2,231	2,234	2,237
84. 88	2,240 2,265 2,292 2319 2.346 2375 2.404 2,434 2.465 2.498	2.242 2.268 2.294 2321 2,349 2,377 2,407 2,437 2.469 2.501	2.245 2.271 2,297 2.324 2,352 2,380 2.410 2.440 2.472 2.505	2.247 2.273 2.300 2.327 2.355 2,383 2.413 2,443 2.475 2.508	2.250 2.276 2.302 2.330 2357 2,386 2,416 2.447 2.478 2.512	2.252 2,278 2,305 2,332 2,360 2.389 2,419 2,450 2,482 2.515	2,255 2.281 2,308 2.335 2,363 2.392 2.422 2.453 2.485 2,518	2,258 2.284 2.3 Ю 2.338 2.366 2.395 2,425 2,456 2.488 2.522	2,260 2.286 2,313 2.341 2,369 2.398 2.428 2,459 2,491 2.525	2.263 2,289 2,316 2,343 2372 2,401 2,431 2.462 2.495 2.529
91 92 93 94 95 96 97 98 99.0	2.532 2.568 2.606 2.647 2.691 2.739 2.793 2.858 2.941	2.536 2.572 2.610 2.651 2.295 2.744 2.799 2.865 2.942	2.539 2.575 2.614 2.655 2.700 2.749 2.805 2.872 2.943	2.543 2.579 2.618 2.659 2.705 2.754 2.811 2.880 2.944	2.546 2.583 2.622 2.664 2.709 2.760 2.818 2.888 2.945	2.550 2.587 2 626 2.668 2.714 2.765 2.824 2.8% 2.946	2.554 2.591 2.630 2.673 2.719 2.771 2.830 2.904 2.948	2.557 2.594 2.634 2.677 2.724 2.776 2.837 2.913 2.949	2.561 2.598 2.638 2.681 2.729 2.782 2.844 2.922 2.950	2 564 2.602 2.642 2.686 2.734 2.788 2.851 2.931 2.951
99.1 99.2 99.3 99.4 99.5 99.6 99.7 99.8 99,9	2.952 2.963 2.974 2.987 3.000 3.015 3.032 3.052 3.078 3.142	2.953 2.964 2.975 2.988 3.002 3.017 3.034 3.054 3.082	2.954 2.965 2.976 2.989 3.003 3.018 3,036 3.057 3.085	2.955 2.966 2.978 2.990 3.004 3.020 3.038 3.059 3.089	2.956 2.967 2.979 2.992 3.006 3.022 3.040 3.062 3.093	2.957 2.968 2,980 2.993 3.007 3.023 3.041 3.064 3.097	2.958 2.969 2.981 2.995 3.009 3.025 3.044 3.067 3.101	2.959 2.971 2.983 2.996 3.010 3.027 3.046 3.069 3.107	2.960 2.972 2.984 2.997 3.012 3.028 3.048 3.072 3.113	2.961 2.973 2.985 2.999 3.013 3.030 3.050 3,075 3.122

Домашнее занятие