Система Maple имеет неограниченные графические возможности – от построения графиков простых функций – в декартовой и полярной системах координат – до создания пересекающихся пространственных объектов.
Maple содержит функцию plot, для построения двумерных графиков (2D типа) и функцию plot3d ( 2D типа) для построения трехмерных графиков. Для обеспечения построения типовых графиков необходимо указать функцию, график которой строится и пределы изменения независимых переменных.
Построение двумерных графиков.
Для построения двумерных графиков служит функция plot(f, h, v) или plot(f, h, v, o),
где f – функция или функции для построения графика, h - переменная с указанием области ее изменения по горизонтали, v - заданная опционально переменная с указанием области изменения по вертикали, o - опция или набор опций, задающих стиль построения графика (толщину и цвет кривых, тип кривых, метки на них и т.д.).
Самыми простыми формами задания этой функции служат:
plot(f, xmin..xmax) – построение графика функции f, заданной только именем;
plot(f(x), x=xmin.. xmax) – построение графика функции f(x).
Диапазон изменения независимой переменной задается как xmin..xmax, где xmin и xmax – минимальное и максимальное значения x,.. (две точки) – составной символ, указывающий на изменение независимой переменной. Имя переменной x – условно. Возможны различные обозначения имени переменных.
Для двумерной графики возможны следующие опции:
axes – вывод различного типа координат (axes=NORMAL – обычные оси, выводятся по умолчанию, axex=BOXES – график заключается в рамку с оцифрованными осями, axes=FRAME – оси в виде перекрещенных линий, axes=NONE – оси не выводятся;
color – задает цвет кривых: red -красный, green - зеленый, blue - синий, black - черный, white - белый, gold - золотистый, yellow -желтый, khaki - хаки и т.д.;
coords – задание типа координатных систем. В частности, задание полярной системы координат производится при помощи опции coords=polar;
numpoints – задает минимальное количество точек графика (по умолчанию numpoints=49);
scaling - задает масштаб графикаCONSTRAINED (сжатый) или UNCONSTRAINED (несжатый) по умолчанию;
size – задает размер шрифта в пунктах;
style - задает стиль построения графика (POINT - точечный, LINE – линиями);
symbol – задает вид символа для точек графика: BOX - mпрямоугольник, CROSS _ крест, CIRCLE - окружность, POINT - точка, DIAMOND - ромб;
title - задает построение заголовка графика (title=”string”, где string – строка);
trickness – определяет толщину линий графиков (0,1,2,3, по умолчанию 0);
view -=[A, B] – определяет мимнимальные и максимальные координаты, в пределах которых график будет отображаться на экране,
A =[xmin..xmax], B=[ymin..ymax] (по умолчанию отображается вся кривая);
xtickmarks - задает минимальное число отметок по оси X;
ytickmarks - задает минимальное число отметок по оси Y.
Пример 1. Построить графики функций, заданных в декартовойсистеме координат  .
.
1) Построение параболы.
Ø plot((x-2)^2,x=-10..10,y=-10..10,title=парабола);

Pис. 1 Парабола
2) Построение графиков двух функций в одной системе координат.
Ø plot([2+(x-2)^3,-(x-4)^2],x=-10..10,y=-10..10);

Рис. 2. Графики двух функций 
Пример 2. Построить график функции, заданной параметрически 
Указание. Используйте функцию plot в следующей форме:
plot([f1(t),f2(t),t=tmin..tmax],h,v,o), где где f – функция или функции для построения графика, h - переменная с указанием области ее изменения по горизонтали, v - заданная опционально переменная с указанием области изменения по вертикали, o - опция или набор опций, задающих стиль построения графика. Если функции f1(t),f2(t) содержат периодические функции, например, тригонометрические, то для получения замкнутых линий, дипазон изменения t задается обычно 0..2*Pi или –Pi..Pi.
Задание указателей масштаба h и v необязательно, но их целенаправленное использование позволяет получить вид графика, удовлетворяющий всем требованиям пользователя.
Построение графика циклоиды, заданной параметрически.
Ø plot([t-sin(t),1-cos(t),t=0..2*Pi],title=циклоида,color=black);

Рис. 3. Циклоида 
Пример 3. Построить линии, заданные уравнениями в полярных координатах 
1) Построение параболы.
Ø plot([4/(1-cos(t)),t,t=0..2*Pi],x=-10..10,y=-10..10,coords=polar);
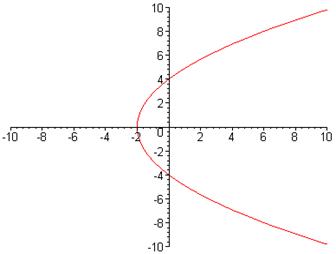
Рис. 4. Парабола  , заданная в полярных координатах
, заданная в полярных координатах
2) Построение кардиоиды.
> plot([3*(1-cos(t)),t,t=0..2*Pi],coords=polar);

Рис.5. Кардиоида 
3) Построение трехлепестковой розы.
> plot([2*sin(3*t),t,t=0..2*Pi],coords=polar);

>
Рис.6. Трехлепестковая роза 
Пример 3. Построить графики функций, заданных неявно 
Указание. Для построения графиков неявных функций используется пакет plots, содержащий около 50 различных функций, среди которых находится функция implicitplot, служащая для построения графиков неявных функций.
1) Построение эллипса.
> with(plots):implicitplot(2*x^2+5*y^2+8*x-10*y-17,x=-10..4,y=-4..4);

Рис.7. Эллипс 
2) Построение гиперболы.
> with(plots):implicitplot(x^2-6*y^2-12*x+36*y-48,x=-20..30,y=-20..20);

Рис.8. Гипербола 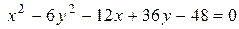
3) Построение линии 
> with(plots):implicitplot(x-1-sqrt(9-y^2),x=-4..10,y=-4..4,color=black,scaling=CONSTRAINED);

Рис.9. Часть окружности 
Построение графиков поверхностей.
Для построения графиков трехмерной поверхности Maple имеет встроенную в ядро функцию plot3d или при помощи пакета plots, содержащего функцию implicitplot3d, предназначенную для построения графиков неявных функций.
plot3d(expr1,x=a..b,y=c..b,p);
plot3d(f,x=a..b,y=c..b,p);
plot3d([exprf, exprh, exprg], s=a..b,t=c..b,p);
plot3d([f,g,h], a..b,c..b,p)
В первых двух формах plot3d применяется для построения обычного графика одной поверхности, в других формах – для построения графика с параметрической формой задания поверхности. В приведенных формах:
f, g, h – функции, выражение, отражающее зависимость от x и y, exprf, exprh, exprg - выражения, задающие поверхность параметрически, s, t, a, b - числовые константы действительного типа, c, d -числовые константы или выражения действительного типа, x, y, s, t - имена независимых переменных, p - параметры-опции, которые задаются аналогично их заданию для функции plot.
Параметры функции plot3d.
axes = - задает вид координатных осей (NORMAL, BOXED, FRAIM, NONE. По умолчанию NONE, без осей.);
lables=[x,y,z] – задает надписи по осям. По умолчанию строки пустые;
view=[xmin..xmax, ymin..ymax, zmin..zmax] или view=zmin..zmax – задает минимальные и максимальные координаты поверхности для ее видимых участков;
tickmarks=[1,n,m] – задает характер маркировки по осям x, y, z. Числа 1, n, m имеют значения не менее 1.
Пример 1. Построить поверхность  , заданную неявно.
, заданную неявно.
> with(plots):implicitplot3d({4*x^2+9*y^2-72*y},x=-10..10,y=-10..10,z=-10..10,axes=NORMAL,tickmarks=[1,5,5]);
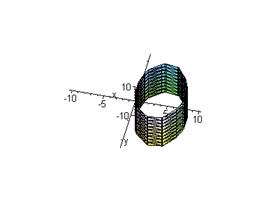
Рис.10 Эллиптический параболоид
Пример 2. Построить поверхность 
Ø with(plots):implicitplot3d({-2*x^2+3*y^2+4*z^2},x=-20..20,y=-20..20,z=-20..20,axes=BOXED,tickmarks=[1,5,5]);
Ø
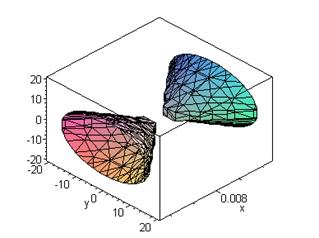
Рис.11 Конусы второго порядка