Построить при помощи Maple:
а) линии, заданные параметрически;
б) линии, заданные в полярной системе координат;
в) график функции, заданной неявно;
г) график функции, изображающий часть кривой второго порядка;
д) построить поверхность, определив ее вид.
Указание. При выполнении заданий в) и д) перед построением графиков заданных функций, необходимо уравнения привести к каноническому виду. При выполнении задания г) перед построением данной кривой необходимо установить, какая линия определяется заданным уравнением, найти область определения этой функции.
Вариант 1
а) 
б) 
в) 
г)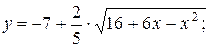 
д) 
Вариант 2
а) 
б) 
в) 
г) 
;
д) 
Вариант 3
а) 
б)
в) 
г) 
д) 
Вариант 4
а) 
б) 
в) 
г) 
д) 
Вариант 5
а) 
б) 
в) 
г) 
д) 
Вариант 6
а) 
б) 
в) 
г) 
д) 
Вариант 7
а)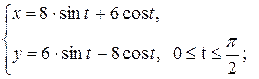 
б) 
в) 
г) 
д) 
Вариант 8
а) 
б) 
в) 
г) 
д) 
Вариант 9
а)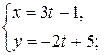 
б)
в) 
г) 
д) 
Вариант 10
а) 
б) 
в) 
г) 
д) 
Вариант 11
а) 
б) 
в) 
г) 
д) 
Вариант 12
а) 
б) 
в) 
г) 
д) 
Вариант 13
а) 
б) 
в) 
г) 
д) 
Вариант 14
а) 
б)
в) 
г) 
;
д)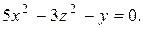 
Вариант 15
а) б) 
в) 
г) 
д)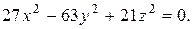 
Пример выполнения задания.
а) Построить кривую, заданную параметрически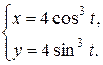 
б) Построить кривую, заданную в полярной системе координат
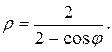
в) Построить кривую 
г) Построить график функции 
д) Определить вид поверхности 
и построить ее.
a) Построение кривой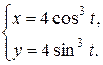
> plot([4*(cos(t))^3,4*(sin(t))^3,t=0..2*Pi],color=black,axes=NORMAL);
Рис.11 Астроида
Получили график астроиды.
б) Построение кривой 
Ø plot([4*(2+cos(2*t)),t,t=0..2*Pi],coords=polar);
Рис.12
в) Перед построением линии 
приведем уравнение к каноническому виду. Для этого выделим полный квадрат в представленном выражении.
Получим далее 
.
Получили каноническое уравнение параболы. Вершина параболы С 
. Ветви направлены вниз, т.к. k=- 2. Построим эту параболу при помощи Maple.
Ø with(plots):implicitplot(8*x^2+24*x+4*y-4,x=-4..4,y=-6..6,scaling=CONSTRAINED,color=black);
>
Рис.13
г) Область определения функции 
Возведем обе части уравнения в квадрат: 
Получили параболу с вершиной в точке с координатами(1/2;0). Строим параболу при помощи Maple. Для этого используем пакет plots, содержащий функцию implicitplot, служащую для построения графиков неявно заданных функций.
Задание в Maple
Ø with(plots):implicitplot(x-sqrt((x-1)^2+y^2),x=0.0..2.0,y=-1.0..1,color=black);
Рис. 14
На рисунке 14 представлена копия экрана с графиком полученной параболы.
д) Определить вид поверхности 
и построить ее.
Выделив полные квадраты при входящих в уравнение переменных (т.е. сгруппировав члены уравнения указанным ниже образом), имеем:
Данная поверхность – двухполостной гиперболоид, который имеет a= 
, b= 
, c= 
, а центр его находится в точке с координатами (-1,-3, 1).
На рисунке 15 представлена копия экрана, изображающего построение этой поверхности в Maple.
 |
Рис. 15
Метод параллельных сечений.
Форма и свойства поверхностей второго порядка устанавливается с помощью метода параллельных сечений. Суть меиода состоит в том, что поверхности пересекаются плоскостями, параллельными координатным плоскостям, а затем по виду и свойствам получаемых в сечениях линий делается вывод о форме и свойствах самой поверхности.
Пример. Установить форму и свойства однополостного гиперболоида 
.
Указание. Для построения сечений этой поверхности и самой поверхности используйте Maple.
Решение. Будем пересекать поверхность z=h горизонтальными плоскостями z=h. Из системы уравнений 
видно, что в любом таком сечении получается эллипс с полуосями 
. Пусть h =1. Построим эллипс при помощи Maple.
> with(plots):implicitplot(x^2/16+y^2/4-1-1/9,x=-5..5,y=-5..5);
Рис. 16
Сечение плоскостями x=h дает гиперболу: 
, а сечение плоскостями y=h дает такую гиперболу: 
. Построение этих гипербол в Maple при значении h =1 представлено на рис.17.
Рис.17
При h=0 получим сечения поверхности (однополостного гиперболоида) координатными плоскостями z= 0, x= 0, y= 0. Эти сечения называются главными. Размеры главных сечений очевидны: в плоскости z= 0эллипс имеет полуоси a=4, b=2; в плоскости x= 0гипербола имеет действительную полуось b =2, мнимую c=3; в плоскости y =0 гипербола имеет действительную полуось a =4 мнимую c =3. Координатные плоскости являются плоскостями симметрии поверхности.
Построим поверхность при помощи Maple.
Ø with(plots):implicitplot3d({x^2/16+y^2/4-z^2/9-1},x=-9..9,y=-9..9,z=-9..9,axes=BOXED)
Рис.18
Построение тел, ограниченных различными поверхностями.
Пример 1. Определить вид поверхностей и построить при помощи Maple тело, ограниченное данными поверхностями 
Решение.
Z =0 – уравнение координатной плоскости 0xy, z=x или x - z=0 – уравнение плоскости, проходящей через начало координат, параллельно оси 0y.
> with(plots):implicitplot3d({z-x},x=-9..9,y=-9..9,z=-9..9,axes=BOXED);
Рис.19
Проекция этой плоскости на на плоскость z0x - прямая линия. Приведем уравнение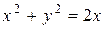 
к каноническому виду. Получим 
Это уравнение цилиндра.
> with(plots):implicitplot3d({x^2+y^2-2*x},x=-2.0..2.0,y=-2.0..2.0,z=0.0..3.0,axes=BOXED);
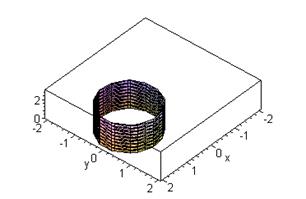
Рис. 20
Строим при помощи Maple тело, ограниченное данными поверхностями.
> with(plots):implicitplot3d({x^2+y^2-2*x,z,z-x},x=-2.0..2.0,y=-2.0..2.0,z=0.0..3.0,axes=BOXED);
Рис. 21