Вычисление объема призмы, параллелепипеда и куба
Внимательно изучите учебную информацию по ссылкам и текст
(Переписывать не нужно!!!
Даже формулы!!! Файл можно открыть в любой момент, не тратим время зря)
https://www.youtube.com/watch?v=PtGiuOrpAX4
https://www.youtube.com/watch?v=kMIrJpF01DM
Расчет объема куба
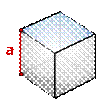
| a- сторона куба
Формула объема куба, (V):
|
Объем прямоугольного параллелепипеда
| a,b,c-стороны параллелепипеда
Формула объема параллелепипеда, (V):
|
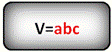
Расчет объема пирамиды
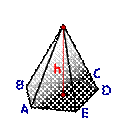
| h- высота пирамиды
S- площадь основания ABCDE
Объем пирамиды, (V):
|
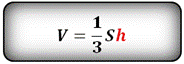
Расчёт объёма усечённой пирамиды
| h- высота пирамиды
Sниж - площадь нижнего основания, ABCDE
Sверх - площадь верхнего основания, abcde
Объем усеченной пирамиды, (V):
|
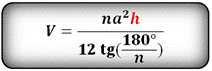
Найти объем правильной пирамиды
| Пирамида в основании, которой лежит правильный многоугольник и грани равные треугольники, называется правильной.
h- высота пирамиды
a- сторона основания пирамиды
n- количество сторон многоугольника в основании
Объем правильной пирамиды, (V):
|
Объем правильной треугольной пирамиды
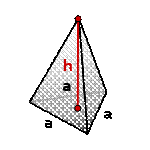
| Пирамида, у которой основание равносторонний треугольник и грани равные, равнобедренные треугольники, называется правильной треугольной пирамидой.
h- высота пирамиды
a- сторона основания
Объем правильной треугольной пирамиды, (V):
|
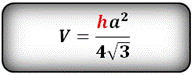
Объем правильной четырехугольной пирамиды
| Пирамида, у которой основание квадрат и грани равные, равнобедренные треугольники, называется правильной четырехугольной пирамидой.
h- высота пирамиды
a- сторона основания
Объем правильной четырехугольной пирамиды, (V):
|
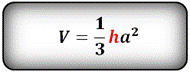
Объем тетраэдра
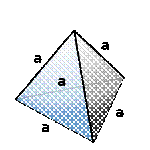
| тетраэдр- пирамида у которой все грани, равносторонние треугольники.
а -ребро тетраэдра
Объем тетраэдра (V):
|
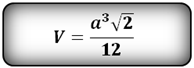
| Прямой параллелепипед, в основании которого лежит параллелограмм со сторонами a, b и углом φ |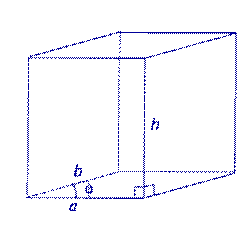 
| Sосн = ab sin φ, V = Sосн h = abh sin φ, где a, b – длины ребер основания параллелепипеда, φ – угол между ребрами основания параллелепипеда, h - высота параллелепипеда. |
| Произвольный параллелепипед |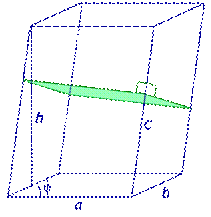 
| Sосн = ab sin φ, V = Sосн h = abh sin φ, V = Sперп с, где a, b – длины ребер основания параллелепипеда, φ – угол между ребрами основания параллелепипеда, c – длина бокового ребра параллелепипеда, h - высота параллелепипеда. |
| Прямая призма |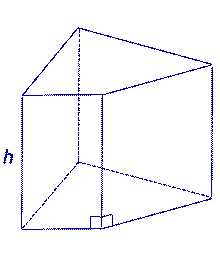 
| V = Sосн h, где h - высота прямой призмы. |
| Правильная n – угольная призма |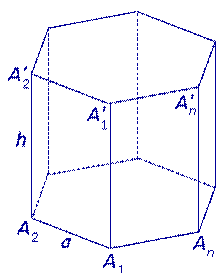 
| 
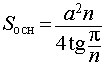V = Sосн h,
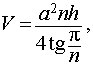где a – длина ребра основания правильной призмы, h - высота правильной призмы.
|
| Произвольная призма |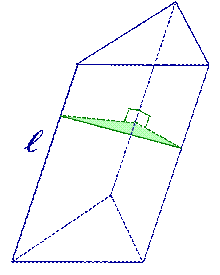 
| V = Sосн h, V = Sперп l, где l – длина бокового ребра призмы, h - высота призмы. |
2. Письменно выполните следующие задания: (Только теперь пишем в тетрадях)
Закончите предложения(Тема: Свойства объемов).
1.Обьем – это_____________________________
2. равные тела имеют ___________________________________________________
3. если тело разбито на части, то его объём равен ___________________________
4. Объём прямоугольного параллелепипеда равен ___________________________
5. Объём любой призмы равен_____________________________________________
6. Два тела называются равновеликими, если они имеют _______________________
2. Ответьте на вопросы и выполните задания.
1. Чему равен объём правильной четырёхугольной призмы, если сторона основания равна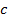 
, а высота призмы –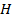 
2. Запишите формулу объёма прямой треугольной призмы, каждое ребро которой равно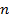 
3. Вычислите объем пирамиды, в основании которой лежит квадрат со стороной 4см, а высота пирамиды – 5 см.