Кратные и криволинейные интегралы
Вариант 1
1. Поменять порядок интегрирования:
Решение:
Пределы интегрирования нам известны, поэтому можем найти границы области интегрирования D, состоящей из двух частей.
Итак, область интегрирования D:
1 часть:
2 часть:
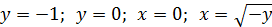
Построим эти области на координатной плоскости.
Область D располагается между прямыми 
и ограничена слева осью ординат, а справа ветвью параболы 
(1 часть); а также между прямыми 
и ограничена слева осью ординат, а справа ветвью параболы 
(2 часть). На рисунке эта область 
заштрихована.
Новые пределы интегрирования должны быть изменены так, чтобы внешний интеграл был от x, а внутренний – от y.
Рассмотрим область интегрирования D на рисунке.
Если ее спроецировать на ось Ox, то ее границами будут точки 0 и 1. Эти точки – пределы внешнего интегрирования.
Снизу область D ограничена параболой , но эту функцию нужно выразить относительно переменной y.
Получим 
.
Сверху область D ограничена параболой или 
.
Запишем двойной интеграл с измененным порядком интегрирования:
2. Вычислить двойной интеграл:
Решение:
Изобразим область интегрирования D на чертеже.
Выберем следующий порядок обхода:
Таким образом, перейдем к повторным интегралам:
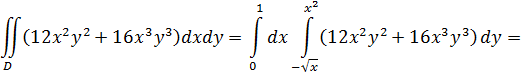
Ответ: 1
3. Вычислить двойной интеграл:
Решение:
Изобразим область интегрирования D на чертеже.
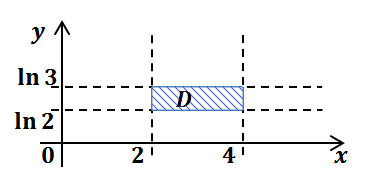
Выберем следующий порядок обхода:
Таким образом, перейдем к повторным интегралам:
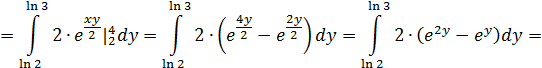
Ответ: 3
4. Найти площадь фигуры, ограниченной линиями:
Решение:
Первые две линии представляют собой окружности. Поэтому для удобства перейдем к полярной системе координат: 
. Тогда все эти линии в полярной системе будут иметь вид:
1) 
2) 
Получается аналогично, то есть 
3) 
4) 
Получается аналогично, то есть 
.
Изобразим фигуру, ограниченную данными линиями, в полярной системе координат.
Площадь фигуры стандартно вычисляется по формуле
Но так как мы перешли к полярной системе координат, то площадь заштрихованной фигуры будем вычислять так:
Выберем следующий порядок обхода:
Таким образом, перейдем к повторным интегралам:
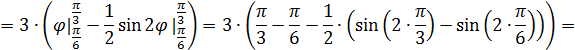
Ответ:
5. Пластинка D задана ограничивающими ее кривыми, 
поверхностная плотность. Найти массу пластинки.
Решение:
Так как пластинка ограничена окружностями, то для удобства перейдем к полярной системе координат: . Тогда все эти линии в полярной системе будут иметь вид:
1) 
2) 
Получается аналогично, то есть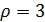 
3) 
4) 
Изобразим фигуру (пластинку), ограниченную данными линиями, в полярной системе координат:
Масса пластинки стандартно вычисляется по формуле
где
Но так как мы перешли к полярной системе координат, то массу пластинки будем вычислять так:
Выберем следующий порядок обхода:
Таким образом, перейдем к повторным интегралам:
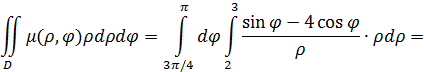
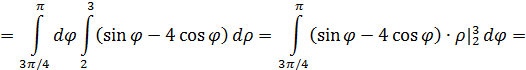
Ответ:
Вычислить криволинейный интеграл
вдоль линии L: отрезок MN от точки 
до точки 
.
Решение:
Сделаем схематический чертеж.
Найдем уравнение прямой, которая содержит отрезок MN. Составим его по двум точкам M и N:
Сведем криволинейный интеграл второго рода к определенному интегралу. Интегрировать будем по переменной x от 2 до 4 по заданному направлению.
Найдем дифференциал уравнения прямой 
.
Подставляя 
в подынтегральное выражение, получим:
Ответ: 8.5