РАСЧЕТ МАСС И МОМЕНТОВ ИНЕРЦИИ ЗВЕНЬЕВ.

ОПИСАНИЕ СТРУКТУРЫПОРШНЕВОГО КОМПРЕССОРА.

Одноцилиндровый поршневой компрессор простого действия предназначен для получения сжатого воздуха. Движение от электродвигателя 7 передается кривошипу 1 через планетарный редуктор 6 и зубчатую передачу z5-z6(рис. а). Преобразование вращательного движения кривошипа в возвратно-поступательное движение поршня осуществляется 6-звенным кулисным механизмом, состоящим из кривошипа 1, кулисного камня 2, вращающейся кулисы 3, шатуна 4 и ползуна (поршня) 5. Изменение давления в цилиндре при движении поршня характеризуется индикаторной диаграммой (рис. б). Всасывание воздуха в цилиндре 8 происходит через впускной клапан 9 во время хода поршня справа налево при давлении ниже атмосферного. Нагнетание сжатого воздуха осуществляется через выпускной клапан 10 при ходе поршня слева направо.

Смазываются механизмы ком-ра плунжерным масляным насосом кулачкового типа. Кулачок 11, закрепленный на одном валу с зубчатым колесом z4, приводит в движения толкателя (плунжерный насос) 12. Для получения требуемой равномерности движения на кривошипном валу закреплен маховик 13. Циклограмма механизмов показана на рис. в.

 

Изм.

Лист

№ докум.

Подпись

Дата

Лист

Описание структуры поршневого компрессора

 

Изм.

Лист

№ докум.

Подпись

Дата

Лист

Описание структуры поршневого компрессора

Предварительная блок-схема.

 

Изм.

Лист

№ докум.

Подпись

Дата

Лист

Расчёт привода

2. РАСЧЕТ ПРИВОДА.

 

2.1. Расчет энергопотребления и определение мощности двигателя:

Привод служит источником механических движений звеньев механизма, причём эти движения должны находиться в полном соответствии с заданной производительностью.

 

Диаграмма нагрузок:

 

 

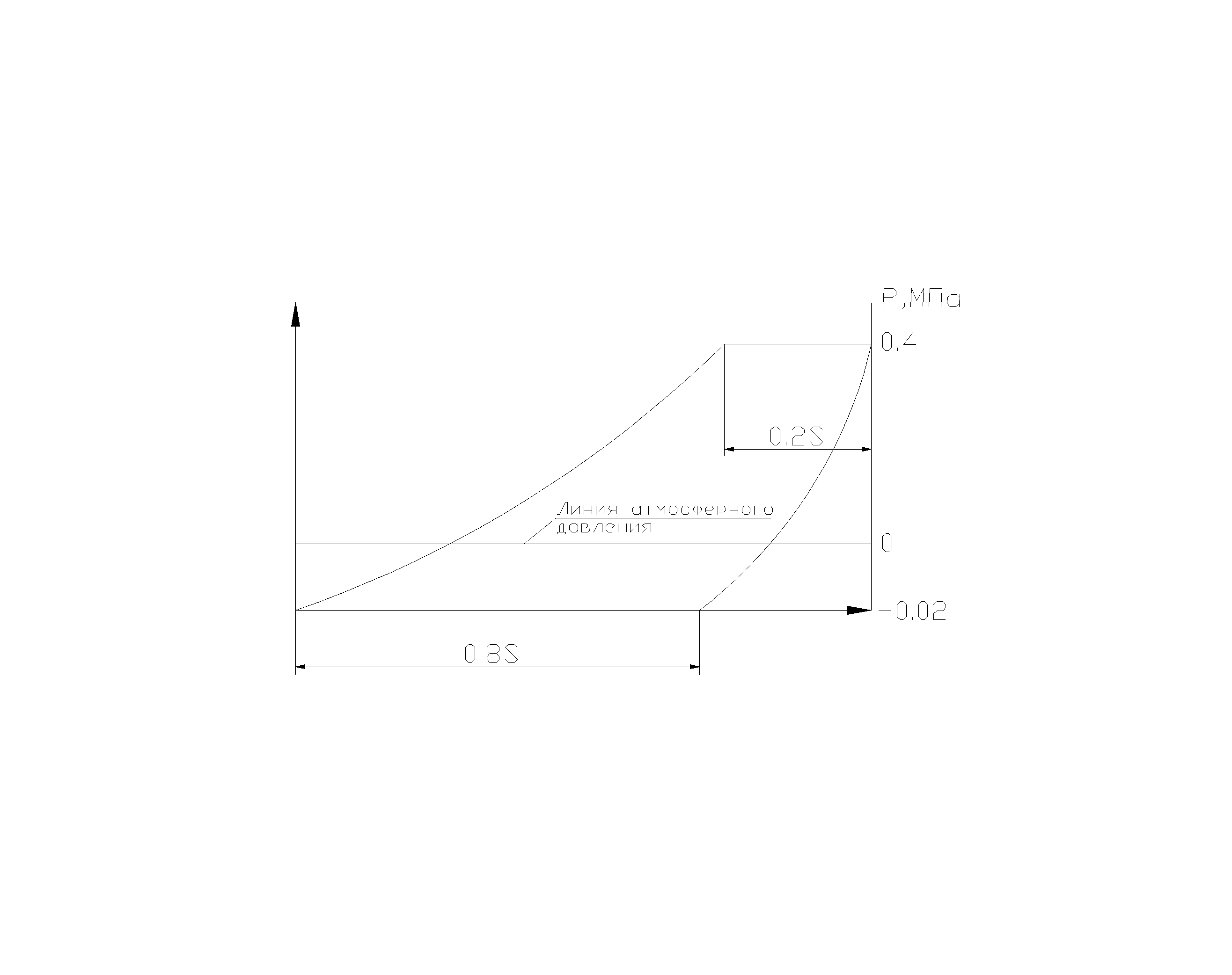
Определяем работу полезной силы:

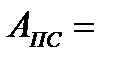
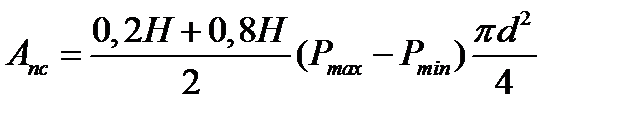
= Дж

Принимаем КПД для компрессора , а КПД электродвигателя

Определяем работу движущих сил:

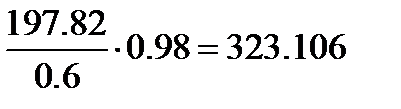Дж

Определяем наполнение цилиндра жидкостью по формуле:

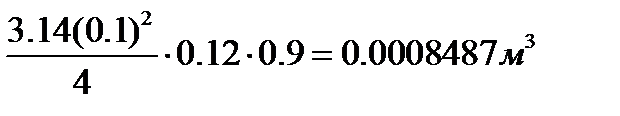
коэффициент наполнения

 

Определяем число циклов компрессора для выпуска 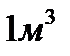воды:

n₁=

Изм.

Лист

№ докум.

Подпись

Дата

Лист

Расчёт привода

Определяем работу, производимую двигателем компрессора за этот период:

 

 

Определяем энергию, потребляемую двигателем из питающей среды:

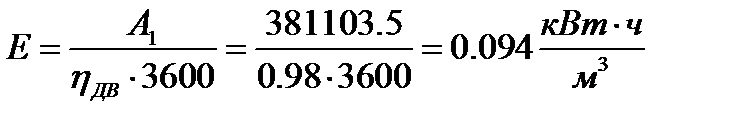
Определяем число циклов компрессора, необходимое для обеспечения требуемой производительности:

n_k=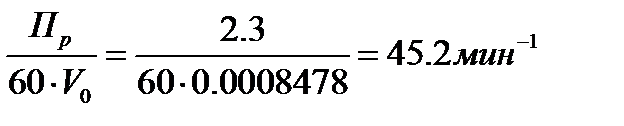

Определяем продолжительность цикла:

Т_ц=

Определяем мощность приводного электродвигателя:

N_дв.=

 

ВЫБОР ЭЛЕКТРОДВИГАТЕЛЯ И ВИДА

ПОНИЖАЮЩЕЙ ПЕРЕДАЧИ.

Из каталога электродвигателей серии 4А выписываем в таблицу параметры электродвигателей с ближайшей мощностью по сравнению с N_дв.=3820 Вт. Для серии 4А:

Изм.

Лист

№ докум.

Подпись

Дата

Лист

Выбор электродвигателя

ТАБЛИЦА 1

Марка эл. двигателя	Ном. Мощ­ность кВт Nном	Частота вращения вала мин-1	Отношение к номинальному моменту	Момент роторакгм2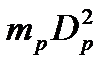
Синхронная nс	Номинальная nном	Пус-ково-го Mп	Критичес-кого Mк
4A56B2Y3	0.25			2.0	2.2	0,00186
100L4У3	0,25			2.1	2.2	0.0049
4A63B6Y3	0,25			2.2	2.2	0,0086

 

Чтобы получить частоту вращения мин^-1, в каждом из случаев привод должен содержать понижающую передачу с передаточным отношением .

Подбираем лучший электродвигатель из трех:

1.

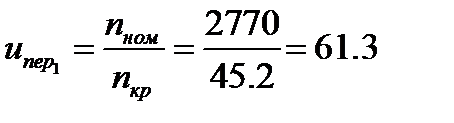
2.

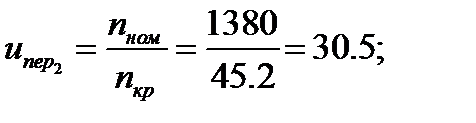
3. .

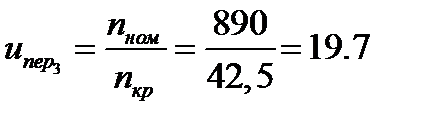Для дальнейших расчетов выбираем двигатель марки 4A63B6Y3 (m=36 кг)

Данные передаточные отношения мы сможем получить, используя одновременно планетарный механизм и простую одноступенчатую открытую передачу. Произведем разбивку общего передаточного отношения следующим образом:

 

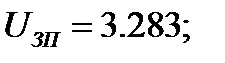
Изм.

Лист

№ докум.

Подпись

Дата

Лист

Синтез зубчатых механизмов

3.1. Синтез зубчатых механизмов.

 

Схема зубчатой передачи представлена на рисунке 1. Основу передачи составляет планетарный механизм с передаточным отношением

Открытая зубчатая передача Z₅-Z₆ имеет передаточное отношение

Синтез планетарного механизма проводим на основе следующих условий:

3.1.1. Планетарный механизм

Условие выполнения требуемого передаточного отношения:

, , , .

 

 

, , , ,

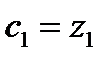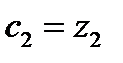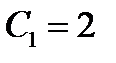1) Условие соосности:

 

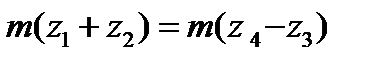
Принимаем q=3

 

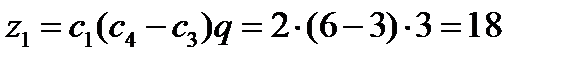
2) Условие соседства:

Число саттелитов может быть k=1,2,3

Условие сборки:

 

При к=3 условие сборки выполняется при любом П, что требует минимального времени на сборку.

 

3) Проверим выполнение условия соседства:

 

Принимаем число саттелитов k=3.

Изм.

Лист

№ докум.

Подпись

Дата

Лист

Синтез зубчатых механизмов

3.1.2 Открытая зубчатая передача

 

Для открытой зубчатой передачи, принимаем Z₅=18, получаем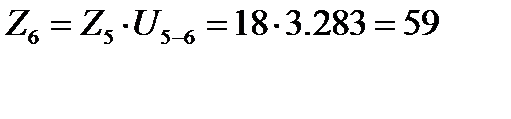

Окончательно принимаем для открытой зубчатой передачи Z₅=18, Z₆=59 зубьев.

Модуль зубчатых колес планетарного редуктора определим по максимальному моменту в зубчатом механизме, который имеет место на выходном его валу. Момент на этом валу ,

где 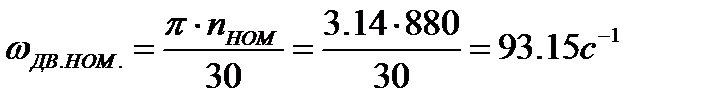-номинальная угловая скорость двигателя.

Модуль зубьев находится по формуле мм берем ближайший больший модуль первого ряда m=1.5 мм.

Модуль зубчатых колес открытой передачи рассчитаем по моменту на валу кривошипа . Учитывая повышенный износ открытой передачи, принимаем мм.

 

 

Определение размеров зубчатых колес.

 

 

Определим делительные диаметры зубчатых колес:

мм

мм

мм

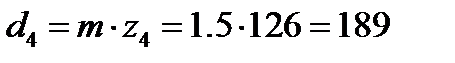мм

мм

мм

Определим диаметр водила принимаем .

Изм.

Лист

№ докум.

Подпись

Дата

Лист

Синтез зубчатых механизмов

Изм.

Лист

№ докум.

Подпись

Дата

Лист

Синтез несущего механизма

3.2 Синтез несущего механизма

Несущий механизм связан с рабочим органом и должен обеспечивать ему возвратно поступательное движение с высоким показателем коэффициента производительности:

=

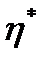Дано: k=1,38; ν_max=24⁰; а=0,015м; υ_ср=3.07м/с

1.Определим угол перекрытия :

Вычислим угол -соответствующий холостому ходу:

, тогда =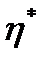

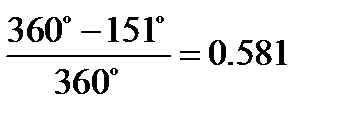
Теперь определим -угол поворота главного вала,соответствующий рабочему ходу рабочего органа:

2.Находим размеры звеньев по следующим формулам:

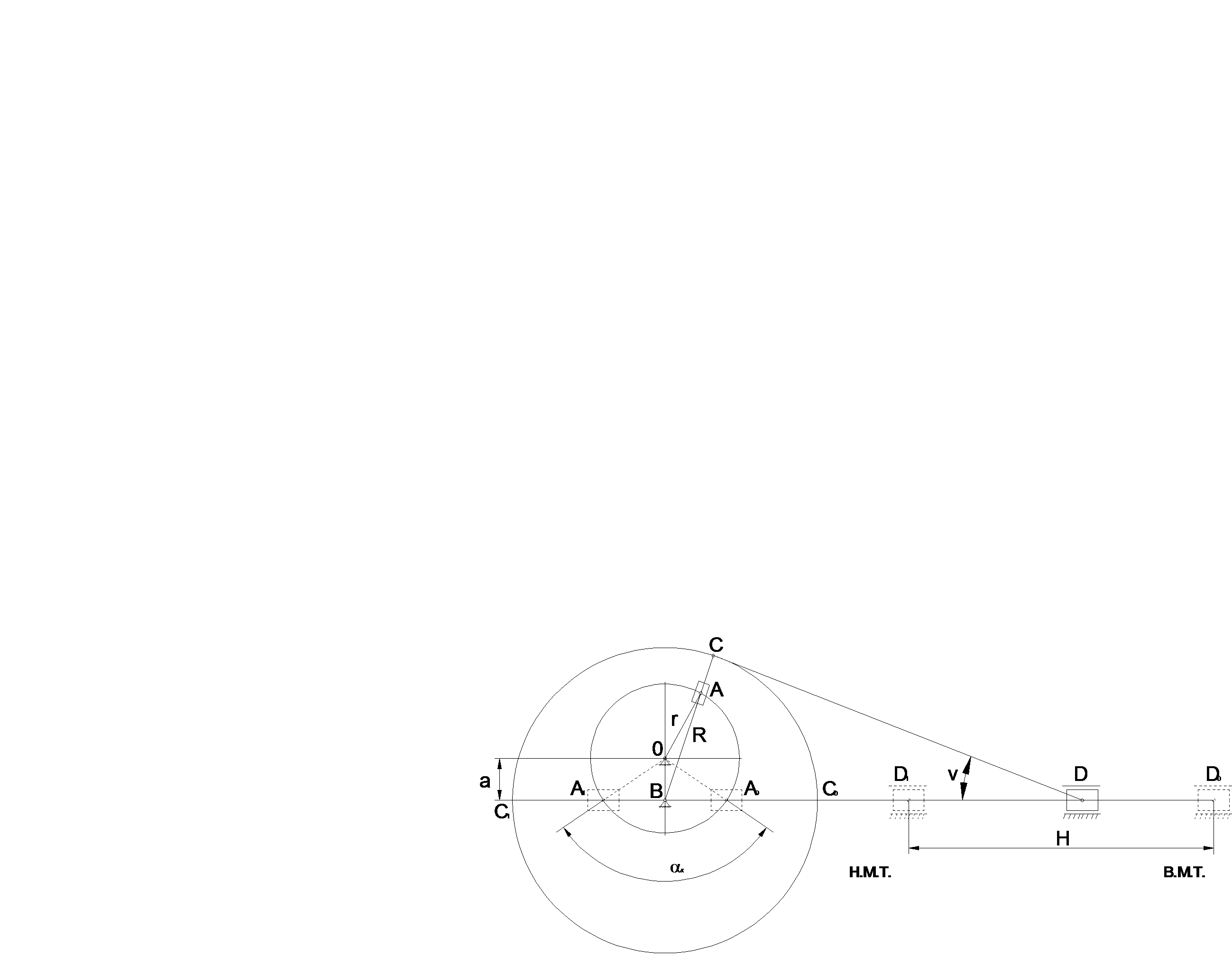Из прямоугольного треугольника OBA: r= м

Длина кулисы ВС: м; Диаметр поршня: d_П=1.5r=0.09м;

Из треугольника СВD найдём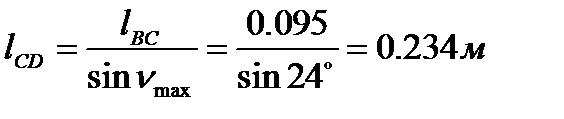

Изм.

Лист

№ докум.

Подпись

Дата

Лист

Синтез кулачкового механизма

3.3Синтез кулачкового механизма

 

Кулачковым называется механизм с высшей кинематической парой, входное звено которого (обычно) называется кулачком, а выходное – толкателем. Он предназначен для преобразования вращательного или поступательного движения кулачка в возвратно-поступательное или во возвратно- вращательное движение толкателя.

Кулачковые механизмы подразделяются по следующим признакам:

1. По расположению звеньев в пространстве (пространственные и плоские).

2. По виду движения кулачка (вращательное, поступательное, винтовое).

3. По виду движения выходного звена (возвратно-поступательное (толкатель); возвратно-вращательное (коромысло))

4. По виду кулачка (дисковый, цилиндрический, коноид (сложный пространственный)).

5. По форме рабочей поверхности выходного звена (плоское, цилиндрическое, сферическое, заострённое, эвольвентное).

6. По способу замыкания ВКП (силовое, геометрическое).

Задача синтеза кулачковых механизмов заключается в определении основных размеров и профиля кулачка по заданным кинематическим и динамическим параметрам.

В нашем случае угол возвращения φ_возв=72⁰; угол удаления φ_уд=90⁰. Эти углы разделены между собой фазовым углом дальнего стояния φ_д.с.=18.⁰

Угол дальнего стояния – угол поворота кулачка, при котором толкатель в крайнем верхнем положении совершает выстой.

Угол возвращения – угол поворота кулачка, при котором толкатель движется из крайнего верхнего положения в крайнее нижнее.

Угол ближнего стояния – угол, при котором толкатель в крайнем нижнем положении совершает выстой.

Выбираем закон движения толкателя кулачкового механизма на фазах удаления и возвращения.

 

 

Изм.

Лист

№ докум.

Подпись

Дата

Лист

Синтез кулачкового механизма

На фазе удаления закон движения Параболический:

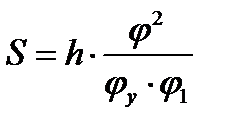при 0≤φ≤ φ_{1; 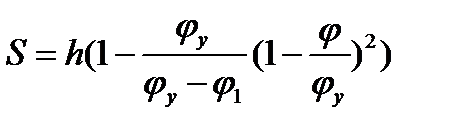при φ1} ≤φ≤ φ_у

График изменения перемещения толкателя

при 0≤φ≤φ_1; 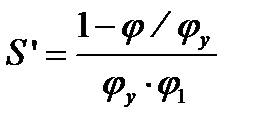при φ₁ ≤φ≤φ_уд

График аналога скорости толкателя

при 0≤φ≤φ_1; при φ₁≤φ≤φ_уд

График изменения аналога ускорения толкателя

 

 

На фазе возвращения модифицированный линейный закон движения:

при 0≤φ≤φ_1; при φ₁≤φ≤ (φ_возв-φ₁₎

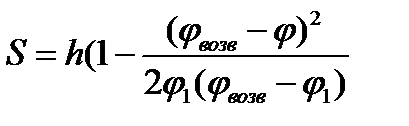при (φ_возв-φ₁₎ ≤φ≤ φ_возв

График изменения перемещения толкателя

при 0≤φ≤φ_1; при φ₁≤φ≤(φ_возв-φ_1);

(φ_возв-φ₁₎≤φ≤φ_возв;

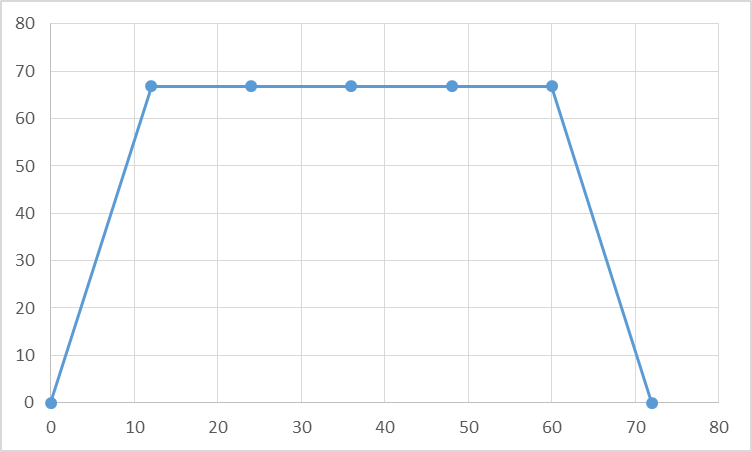
График аналога скорости толкателя

Изм.

Лист

№ докум.

Подпись

Дата

Лист

Синтез кулачкового механизма

при 0≤φ≤φ_1; 0 при φ₁≤φ≤(φ_возв-φ_1); при(φ_возв-φ₁₎ ≤φ≤ φ_возв

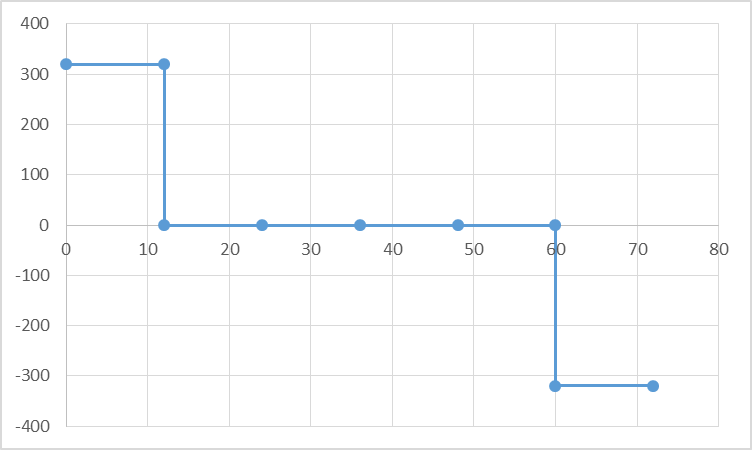
График изменения аналога ускорения толкателя

Результаты расчётов заносим в таблицу 2:

Фаза	i	k	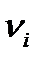,0		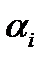		,0	,0	Ri,мм
Удаление							-30
			0.3876	7.295	89.807	-23.331	8.997	59.336
			2.9181	26.394	145.31	-3.291	17.976	61.545
			8.9181	50.001	145.31	18.86	26.933	66.873
			18.387	69.099	89.807	29.679	35.878	75.486
				76.394			44.825	86.295
			41.613	69.099	-89.807	23.129	53.784	97.289
			51.082	50.001	-145.31	11.345	62.757	106.351
			57.082	26.394	-145.31	-1.645	71.743	112.128
			59.613	7.295	-89.807	-11.341	80.737	114.572
						-14.871	89.736	114.946
Возвращение						227.97	---------	107.736	114.946
			55.556	39.789	151.98	---------	119.746	110.657
			44.444	63.662	75.991	---------	131.776	99.991
				71.62		---------	143.728	86.295
			15.556	63.662	-75.991	---------	155.893	72.889
			4.444	39.789	-151.98	---------	167.965	62.888
					-227.97	---------

Определим основные размеры и е кулачкового механизма по условию ограничения угла давления только на фазе удаления, так как высшая пара имеет силовое замыкание и кулачок вращается против часовой стрелки. В этом случае воспользуемся следующими формулами:

Для равноубывающего удаления толкателя угол, при котором имеет наибольшее значение, 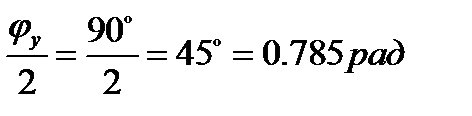, а аналог скорости и перемещение , соответствующие этому углу,

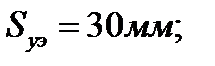
Подставив эти значения в формулы, получаем:

Изм.

Лист

№ докум.

Подпись

Дата

Лист

Синтез кулачкового механизма

Принимаем ; При вращении кулачка против часовой стрелки положительному значению смещения е соответствует расположение линии движения справа от центра вращения кулачка.

Определяем по формуле угол давления только на фазе удаления

Изм.

Лист

№ докум.

Подпись

Дата

Лист

Синтез кулачкового механизма

, так как высшая пара имеет силовое замыкание и заклинивание механизма может произойти только на фазе удаления (на фазе возвращения толкатель движется под действием пружины).

Так как 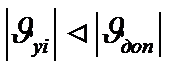,то значения и е удовлетворяют условию синтеза.

Определяем полярные координаты центрового профиля кулачка по формулам:

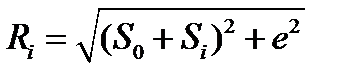
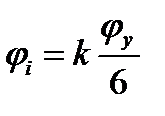где на фазе удаления , а на фазе удаления , к изменяется от 0 до10.

Результаты расчетов заносим в таблицу 2. По полученным значениям и строим центровой профиль кулачка. Для этого в масштабе проводим ок-

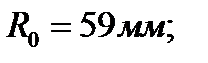
ружности радиусами: ; 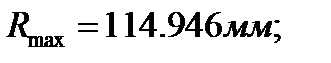Касательно к окружности радиусом е слева проводим линию движения толкателя уу. Соединив точку пересечения направляющей уу с окружностью радиусом 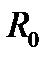(точку 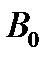) с центром вращения кулачка (точка ), получим радиус-вектор , соответствующий началу удаления. От этого радиуса в направлении, противоположном вращения кулачка, отложим полярные углы , на сторонах, которых строим в масштабе 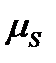радиусы-векторы .

Соединив плавной кривой концы радиус-векторов, получим центровой профиль кулачка.

На фазе дальнего стояния кулачек очерчивается дугой радиусом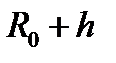

На фазе возвращения построение аналогично построению на фазе удаления.

На фазе ближнего стояния профиль очерчивается радиусом

Определим минимальный радиус кривизны центрового профиля кулачка как радиус вписанной окружности выпуклого участка профиля кулачка, где кривизна его окажется наибольшей. На этом участке произвольно выбираем три точки , и и соединяем их двумя хордами. В середине хорд восстанавливаем к ним перпендикуляры, точку пересечения которых М принимаем за центр вписанной окружности.

Действительный профиль кулачка найдем как эквидистантную кривую, отстоящую от центрового профиля на расстоянии, равном радиусу ролика.

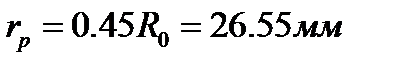
Окончательно выбираем

Для получения действительного профиля кулачка на его центровом профиле выбирается ряд точек, из которых проводим полуокружности (в сторону уменьшения радиуса-вектора кулачка) радиусом ролика . Огибающая этих полуокружностей и является действительным профилем кулачка.

Рассчитаем характеристики замыкающей пружины. Для определения силы пружины и ее жесткости построим график сил инерции толкателя 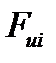в функции перемещения 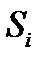(Рис.9).

Для расчета выбираем фазу удаления, так как на этой фазе аналог ускорения толкателя имеет наибольшее значение , чем на фазе возвращения. Для закона с равноубывающим удалением толкателя:

Сила инерции толкателя: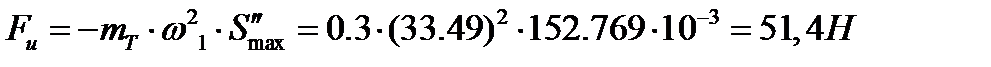

где = 5h=300г,

а угловая скорость кулачка: ,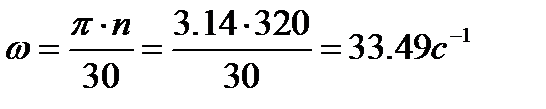

где

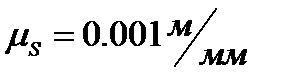Принимаем минимальную реакцию а предварительное напряжения пружины . Выбрав масштабные коэффициенты и , производим построение рис. Соединив точки a и b, получим зависимость . Максимальная сила пружины 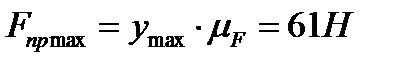. Жесткость пружины:

Изм.

Лист

№ докум.

Подпись

Дата

Лист

Синтез кулачкового механизма

 

 

Изм.

Лист

№ докум.

Подпись

Дата

Лист

РАСЧЕТ МАСС И МОМЕНТОВ ИНЕРЦИИ ЗВЕНЬЕВ

4. ДИНАМИЧЕСКИЙ СИНТЕЗ

Динамический синтез компрессора проводят с целью повышения его общего к.п.д. путём снижения теплового излучения обмоток приводного электродвигателя при неравномерном вращении ротора внутри цикла.

Задачу решают путем подбора и перераспределения масс звеньев, введением, при необходимости, дополнительной маховой массы с постоянным моментом инерции в виде маховика. Предварительно анализируют инертные свойства имеющихся механизмов.

 

РАСЧЕТ МАСС И МОМЕНТОВ ИНЕРЦИИ ЗВЕНЬЕВ.

Инертные свойства звеньев характеризуют показатели массы (при поступательном движении) и момента инерции (при вращательном).

В первом приближении можно принять, что по длине рычагов массы распределены равномерно, что интенсивность распределения q = 30 кг/м и что зубчатые колёса – сплошные диски с шириной b_k, зависящей от межосевого расстояния a_w, как:

, где - коэффициент ширины зуба.

Центры масс рычагов располагаются по их серединам, массы определяются как: m_i = q×l_i

Моменты инерции звеньев относительно их центров масс находим как:

а относительно оси вращения (для вращательных звеньев): .

Массы зубчатых колёс определяются через делительные диаметры и межосевые расстояния a_w по формуле: , где

Моменты инерции зубчатых колёс относительно оси вращения определим через их массу и делительные диаметры как для однородных дисков по формуле: .

Оценку динамических характеристик прочих деталей компрессора производим следующим образом:

1. Массу ползуна:

2. Массу водила планетарной ступени редуктора: ,

где ширину водила принимаем равной:

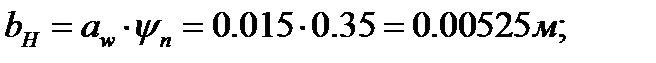
C учётом этого: 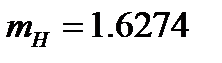кг

Момент инерции определяем как для сплошного диска:

Массу кулачка m_k и момент инерции I_к оцениваем по среднему его радиусу:

и ширине b_k, которую мы задаём как:

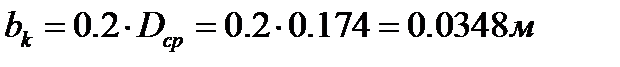
В этом случае:

а момент инерции

I_k = m_k×D²_ср/8=0.0244кг×м²

Момент инерции ротора определяем по маховому моменту

m_p·D²_p=2.37·10^-2кг×м³.

Получаем:

I_p = m_pD²_p/8=0.00296кг×м².

 

 

Изм.

Лист

№ докум.

Подпись

Дата

Лист

РАСЧЕТ МАСС И МОМЕНТОВ ИНЕРЦИИ ЗВЕНЬЕВ

Динамические характеристики остальных движущихся звеньев из-за малых их масс, либо скоростей точек, считаем пренебрежимо малыми и далее не учитываем. Полученные результаты расчётов заносим в таблицу 4.1.

 

Наименование звена	Обозначение звена	Наименование параметра и его обозначение
Длина рычага, диаметр колеса, м	Масса, кг	Момент инерции относительно оси вращения, кг×м2.	Момент инерции относительно центра масс, кг×м2.
Рычаг	ОА ВС СD	кривошип, 0.06 вращ. кулиса, 0.095 шатун, 0.234	1.8 (m1) 2.85 (m3) 7.02 (m4)	0.00216(I01) ______ ______	_______ 0.0021(Is3) 0.032(Is4)
Зубчатые колёса	Z1 Z2 Z3 Z4 Z5 Z6	d1 =0.045 d2 =0.18 d3 =0.225 d4 =0.45 d5 =0.08 d6 =0.096	0.651 (mz1) 1.0415 (mz2) 1.6274 (mz3) 6.5095 (mz4) 0.2057 (mz5) 0.2963 (mz6)	0.000165 0.00422 0.0103 0.1648 0.000165 0.000341
Ползун	D	___	7.02 (m5)	___	___
Водило	H	___	1.6274 (mH)	0.0103(IH)	___
Кулачок	K	___	6.45 (mk)	0.0244(Ik)	___
Ротор		___		0.00296(Ip)	___

Таблица 4.1.

Изм.

Лист

№ докум.

Подпись

Дата

Лист

РАСЧЕТ МАСС И МОМЕНТОВ ИНЕРЦИИ ЗВЕНЬЕВ