Содержание
Введение. 2
Основная часть. 4
Историческая справка о розах Гвидо Гранди. 4
Полярная система координат. 6
Связь между полярной и декартовой системами координат. 6
Переход от полярной системы координат к декартовой. 7
Розы Гвидо Гранди. 7
Понятие кривой. 7
Связь с другими кривыми. 9
Исследование кривой в зависимости от изменения параметров. 10
Разнообразие роз Гвидо Гранди. 11
Заключение. 16
Список использованной литературы.. 17
Введение
Математика-это наука, которая изучает величины, количественные отношения и пространственные формы, описывает процессы, происходящие в окружающем нас мире. Законы математики и решения математических задач приложены ко всем областям человеческой деятельности. Линии занимают особое положение в математике. Используя линии, можно создать наглядные модели многих процессов и проследить их течение во времени. Линии позволяют установить и исследовать функциональную зависимость между различными величинами. С помощью линий удается решать многие научные, инженерные задачи в различных отраслях жизни. Нас заинтересовали кривые, заданные в полярных координатах. Среди них можно назвать спираль Архимеда, кардиоиду, астроиду, розы Гвидо Гранди. Больше других наше внимание привлекла математическая кривая, похожая на цветок- полярная роза или роза Гвидо Гранди, и мы в своей работе хотим исследовать многообразие форм «роз» Гвидо Гранди.
Данная работа является актуальной, так как позволяет расширить знания о свойствах таких замечательных кривых, как розы.
Объектом исследования является кривая роза Гвидо Гранди.
Предмет исследования – зависимости кривых Гвидо Гранди от различных значений параметров.
|
|
Цель работы: исследовать, как изменяются кривые Гвидо Гранди, заданные в полярной системе координат в зависимости от различных значений параметров.
Задачи:
1. Исследовать связь между количеством липестков, их формул и симметричности получившегося рисунка;
2. Показать с помощью компьютерной среды Microsoft Excel, как изменяются кривые в зависимости от различных значений параметров;
3. Получить большое разнообразие форм «роз» Гвидо Гранди;
4. Провести анализ полученных данных и сделать выводы.
Основная часть
Историческая справка о розах Гвидо Гранди
В 18 веке итальянский геометр Гвидо Гранди (1671-1742) создал кривые линии с правильными плавными очертаниями. Они были похожи на цветок. Семейство этих кривых было названо семейством роз Гвидо Гранди. Их правильное очертание-это не каприз природы- они предопределены математическими зависимостями. Эти зависимости были подсказаны самой природой, ведь в большинстве случаев абрис листа или цветка представляет собой кривую, симметричную относительно оси. Свои прекрасные цветы Гвидо Гранди собрал в одну книгу и назвал ее «Цветник роз». Гранди известен своей работой Flores geometrici (1728), изучавшей розы - кривые, которые имеют форму лепестков цветка. Он назвал розы кривой rhodonea и назвал кривую Clelia в честь графини Клелии Борромео.
Уравнение розы Гвидо Гранди в полярных координатах имеет вид: 
.
Задавая параметр 
отношением натуральных чисел можно получить замкнутые кривые, при определенных условиях превращающиеся в лепестковые цветы или в ажурные розетки, которые могут служить элементами декора или орнамента.
|
|
Очарованный результатами Гранди, немецкий геометр, математик-натуралист XIX в. Б. Хабенихт также решил заняться математическим «растениеводством». И он путем многочисленных экспериментов «вырастил» замечательные экспонаты. Полагая, что абрис (очертание) листа или цветочного лепестка в полярных координатах описывается выражением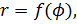 
где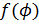 
для каждого отдельного растения представляет определённую комбинацию тригонометрических функций, Хабенихт в своих работах приводит ряд полученных им уравнений, которые с хорошим приближением аналитически выражают очертания различных листьев и плодов. Он также рассматривает контур листа как замкнутую кривую, которая в полярной системе координат имеет уравнение.
Если предположить, что кривая, изображающая контур листа, симметрична относительно полярной оси, а функция является конечной суммой, то эта сумма должна состоять из косинусов или синусов. Исходя из этого общего уравнения, Хабенихт исследует его частные случаи. Постепенно усложняя уравнение он получает большое количество уравнений контуров листьев: плюща, крапивы, листьев кислицы и др.