В полярной системе координат положение точки определяется полярным радиусом R и углом j, образуемым полярным радиусом с полярной осью. Следовательно, полярная система координат — система координат, ставящая в соответствие каждой точке на плоскости пару чисел (R;j). Основными понятиями этой системы являются точка отсчёта (полюс) и луч, начинающийся в этой точке (полярная ось).
Если в декартовой системе координат предельно простое выражение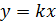 
определяет прямую линию, то это же выражение, переписанное в форме 
, уже превращается в спираль. Фигуры в полярных координатах образуются как след конца бегающего по кругу полярного радиуса переменной длины. Длина полярного радиуса определяется величиной угла, который в данный момент времени он образует с полярной осью. Координата j берётся со знаком «+», если угол от оси до отрезка вычисляется против часовой стрелки, и со знаком «-» в противоположном случае. Любая точка в этой системе имеет бесконечное число координат вида 
, которым соответствует одна и та же точка при любых натуральных n. Для полюса r = 0, угол j произвольный.
Связь между полярной и декартовой системами координат.
Точка О - полярный полюс, луч ОЕ будем называть полярной осью, отрезок ОМ - называют длиной полярного радиуса R, положительный угол от луча ОЕ до луча F - полярный угол.
Если известны полярные координаты R и j, точки М, то можно уставить связь с её декартовыми координатами. Построим прямоугольный D ОМЕ. В этом треугольнике гипотенуза ОМ=R, ÐЕОМ = j, катет ЕМ = у, катет ОЕ = х координаты точки М. Для того, чтобы перейти от полярных координат к декартовой системе, используют формулы: 
, 
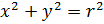. Обратно, чтобы, имея прямоугольные координаты, получить расстояние нужное для задания полярных координат, надо воспользоваться теоремой Пифагора: 
, затем 
, 
. Построение кривых, заданных полярными уравнениями, имеет некоторые специфические особенности, которые мы проиллюстрируем на примерах.
|
|
Переход от полярной системы координат к декартовой
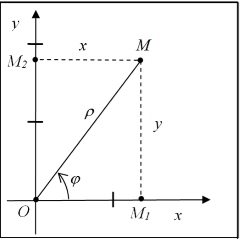
Если полюс полярной системы координат совместить с началом прямоугольной системы координат, а полярную ось с положительной полуосью Ox, то по известным полярным координатам точки 
её прямоугольные координаты вычисляются по формулам:
, 
.
Розы Гвидо Гранди
Понятие кривой
Для начала вспомним понятие кривой.
Кривая линия – это множество точек пространства, координаты которых являются функциями одной переменной. Каждая кривая включает в себя геометрические элементы, которые составляют её определитель, т.е. совокупность независимых условий, однозначно определяющих эту кривую. Мы знакомы с некоторыми алгебраическими плоскими кривыми, с такими как парабола, гипербола, эллипс и т.д. Плоские кривые - это кривые линии, все точки которых принадлежат одной плоскости. Плоская кривая линия называется алгебраической, если её уравнение 
.
Парабола Гипербола Эллипс
Роза Гвидо Гранди — плоская кривая, заданная в полярной системе координат, напоминающее символическое изображение цветка.
Впервые исследованием роз занимался итальянский геометр Гвидо Гранди. Полная теория этих кривых была изложена им в сочинении «Flores geometrici ex rhodanearum et claelarum deskriptione resultants», изданном в 1728 году.
Задача.
Отрезок длины 
движется так, что его концы все время находятся на координатных осях. Составить уравнение траектории основания М перпендикуляра, опущенного из начала координат на отрезок. Решением данной задачи будет уравнение так называемой четырехлепестковой розы 
или 
.
|
|
В полярных координатах общее уравнение для роз записывается в виде: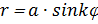 
или в виде 
, где a и k – положительные числа.
Связь с другими кривыми.
Замечательные кривые
Кардиоида
Кардиоида (от греческих слов сердце и вид) – получила свое название из-за схожести своих очертаний со стилизованным изображением сердца.
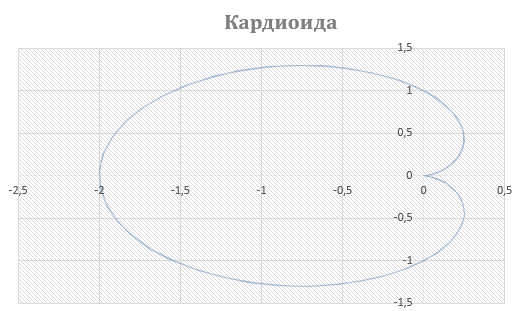Кардиоиду можно построить и другим способом. Она описывается фиксированной точкой окружности, катящейся по неподвижной окружности с таким же радиусом.
Определяется уравнением в полярных координатах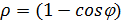 
.
(a - радиус окружности)
Полярная роза – известная математическая кривая, похожая на цветок.
Определяется уравнением в полярных координатах 
.
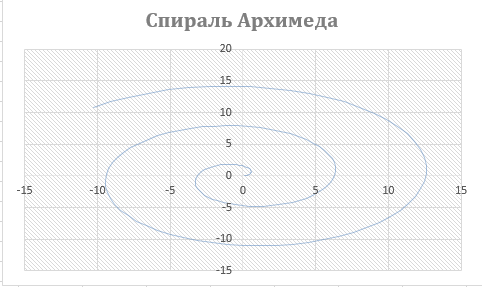Спираль Архимеда – названа в честь ее изобретателя, древнегреческого математика Архимеда. Определяется уравнением в полярных координатах
.