Рассмотрим уравнение кривой 
Возьмём для начала любое 
-чётное число, тогда получим «розу» с количеством лепестков 
, и длина от начала координат до вершины лепестков будет равна радиусу описанной окружности 
. Кривые симметричны относительно оси ординат, оси абсцисс и начала координат.
Если мы возьмём любое и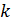 
-нечётное число, то получим цветок из 
лепестков. Мы замечаем, что в одном случаи есть лепесток, направленный по оси ординат вверх, а в другом вниз. Это зависит от значения k. Вниз лепесток будет направлен при 
и при всех последующих нечётных через одно число, вверх – при 
и при всех следующих нечетных числах через одно. Кривые симметричны относительно оси ординат.
Рассмотрим уравнение кривой 
Мы замечаем, что количество лепестков стало зависеть от c и b. Если 
, а 
получаем кривую, напоминающую 2 кардиоиды, "наползшие" друг на друга. Если 
, то мы получим кардиоиду с петлей "внутри себя". Если 
мы получим закольцованную спираль, в центре которой будет кардиоида(1 или 2). Если 
, c-любое нечётное число, b-любое нечётное число и получившаяся дробь не сокращается до целого числа, тогда мы получаем «розу» с c-лепестков, у которого они находят друг на друга. При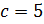 
и всех последующих нечётных чисел через одни, один лепесток «розы» будет направлении вниз по оси ординат. По аналогии при 
и при всех последующих нечётных числах один лепесток направлен вверх по оси ординат. Кривая симметрична относительно оси ординат.
Если , c-любое чётное число, b-любое нечетное и получившаяся дробь не сокращается до целого числа, то мы имеем «розу» из лепестков количеством 
. Они ложатся друг на друга. Кривые симметричны относительно начала координат, оси ординат и абсцисс.
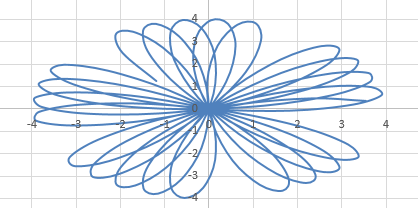
Если мы зададим значения , c-любое нечётное число, b-любое чётное и получившаяся дробь не сокращается до целого числа, тогда увидим цветы с количеством лепестков . Они будут накладываться друг на друга. Кривые симметричны относительно начала координат, оси ординат и абсцисс.
Рассмотрим уравнение кривой 
Если k-чётное число, и мы будем прибавлять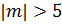 
, то наша «роза» из лепестков будет переходить в кривую, стремящуюся к форме окружности. Чем больше m и чем меньше n, тем более округленный цветок мы получим:
Если k-нечётное число, и если будем прибавлять числа |m|>5, то наша кривая в форме цветка будет переходить в окружность. Чем больше m и чем меньше n, тем более округленный цветок мы получим.
Также в полярных координатах можно описать при помощи косинусов кратных дуг линии, которые обрисовывают контуры листьев некоторых растений:
· Кувшинки: 
· Кислицы: 
.
· Настурции: 
.
· 
Стрелолиста: 
.
Заключение
В данной работе мы приведена классификацию кривых Гвидо Гранди и описаны их основные свойства.
Исследовав, как изменяются кривые Гвидо Гранди, заданные в полярной системе координат в зависимости различных значений параметров 
, мы установили связь между количеством лепестков, их формул и симметричности получившегося рисунка. Когда мы получали «розы» из четного количества лепестков, рисунок был симметричен относительно начала координат и осей координат. Если мы получали цветы из нечётного количества лепестков, то рисунок был симметричен только оси ординат.
Список использованной литературы
1. Савелов А.А. Плоские кривые. Систематика, свойства, применение
2. https://matematikaiskusstvo.ru/rosesgrandy.html
3. https://sibac.info/11124
4. https://gvidograndi.jimdo.com/ Как строить графики в полярных координатах.