Вопрос 1.
События и вероятность.
Событие – всякий факт, который в результате опыта (испытания, эксперимента) может произойти или не произойти.
Таким образом, событие – это исход опыта.
Например: опыт – бросание монеты, событие – выпадение орла или решки.
Вероятность события – численная мера степени объективной возможности этого события. U (достоверное событие) – которое в результате опыта непременно произойдет. V (невозможное событие) – которое не может произойти в результате опыта.
3 подхода к определению понятия вероятности:
1. классический (подсчет вероятности)
2. статистический (частотный)
3. аксиоматический (теоретико-множественный)
Классический.
Несовместное событие – если появление 1 из них исключает появление других событий в одном и том же опыте.
Полная группа событий: события в опыте образуют полную группу, если в результате опыта произойдет хотя бы 1 из них (например, попадание или промах, орел или решка).
А1 = {1 или 2 или 3}, А2 = {3 или 4 или 5}, А3 = {4 или 5 или 6} – полная группа совместных событий.
Равновозможные события: события в опыте называются равновозможными, если по условиям симметрии есть основания считать, что ни 1 из этих событий не является объективно более возможным, чем другие.
События, обладающие всеми тремя свойствами, называются случаями.
Для каждого опыта можно указать некоторую совокупность взамноисключающих друг друга элементарных исходов. Причем в результате 1 опыта должен осуществится какой-нибудь 1 из них. Эту совокупность и называют совокупностью всех элементарных исходов опыта.
А={1 или 2 или 3}-составное
Если элементарные исходы равновозможные, то это случаи. Тогда опыт сводится к схеме случая. И для таких опытов возможен непосредственный подсчет вероятностей. Он основан на подсчете благоприятных случаев.
Случай является благоприятным событию, если его появление влечет появление данного события.
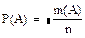 (1.1)
(1.1)
m(А)-число благоприятных случаев
n-общее число случаев
Р(А)-вероятность события А
Р(А)=3/6 – для игр в кости(четный случай)
(1.1) – только для схемы случая
(1.2)  , следовательно
, следовательно 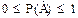
Р(V)=0
P(U)=1
Пример: в мешке 2 белых и 3 черных шара. Найти вероятность достать белый шара?
А – белый шар
Так как извлекаем наугад, то опыт сводится к схеме случая.
n=5
m(A)=2
P(A)=2/5
Частотный подход основан на понятии частоты. Это опытный подход. Частотой события А в данной серии опытов называем отношением числа опытов, в которых произошло данное событие к общему числу опытов.
(1.3) Р* (А)=m(А)/n
Р* - частота А
m(А) – опыты, в которых произошло А
n – число опытов
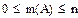 , следовательно 0≤Р*≤1
, следовательно 0≤Р*≤1
Р*(V)=0
Р*(U)=1
Частота имеет свойство устойчивости.
Величина, около которой стремится стабилизироваться частота А при увеличении n называется вероятностью события.
Рассмотрим 2 несовместных события А1 и А2. m(А1 или А2)=m(А1)+m(А2)
Р*(А1 или А2)= m(А1 или А2)/n=m(А1)/ n+m(А2)/ n= Р*(А1)+ Р*(А2) (1.6)
Вопрос 2.
Аксиоматическое строение теории вероятности.
В основе лежит построение математической модели случайного эксперимента. При введении аксиом используется частотный подход.
Случайный эксперимент->модель случайного эксперимента
Множество элементарных исходов->пространство элементарных событий 
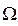 ={
={  }
}
 1={ЦЦ}
1={ЦЦ}
 2={ГЦ}
2={ГЦ}
 3={ЦГ}
3={ЦГ}
 4={ГГ}
4={ГГ}
Множества 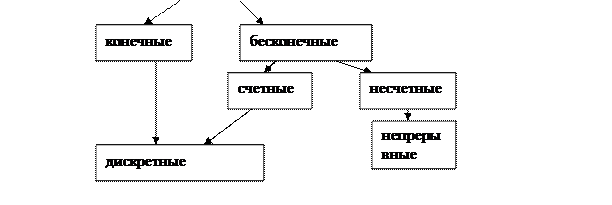
Счетные – можно поставить в соответствии натуральных чисел, то есть пронумеровать.
Например, бросание монеты до появления герба
 1={Г}
1={Г}  2={ЦГ}
2={ЦГ}  3={ЦЦГ} …
3={ЦЦГ} …
Непрерывные – когда заполняется полностью интервал.
Подмножества пространства  называются событиями. Таким образом любое событие
называются событиями. Таким образом любое событие  в точке
в точке  i, составляющие событие А называются благоприятствующими события А или входящими в событие А.
i, составляющие событие А называются благоприятствующими события А или входящими в событие А.
А – выпадение герба.
А={ω2+ ω 3}
UóΩ А=А1∙А2
Vó0
Построение алгебры событий позволяет изображать случайные события через простые.


 Если всякий раз, когда происходит событие А происходит и событие В, то говорят, что А входит в В.
Если всякий раз, когда происходит событие А происходит и событие В, то говорят, что А входит в В.
А и В – несовместные, так как
не имеют общих точек. Ω
Диаграмма Венна


 Ω
Ω
А входит в В =>
Если каждый раз, когда происходит событие А, происходит событие В и,когда происходит В, происходит и А, то говорят, что события А и В равносильны или эквивалентны.
Ω

 А=В
А=В
Суммой событий А и В называют событие С, наступающее тогда, когда наступает хотя бы 1 из событий А или В.
С=А+В→(теоретико-множественный подход)→С=АUВ (объединение)
 |
Ω
 Произведением А и В называется событие С, наступающее тогда, когда наступает событие А и В.
Произведением А и В называется событие С, наступающее тогда, когда наступает событие А и В.
 С=АВ→(ТМП)→А∩В
С=АВ→(ТМП)→А∩В
 Ω
Ω
А+А=А А∙А=А А+U=U А∙ U= А А+V=А А∙ V= V
АUА=А А∩А=А А+Ω=Ω А∩Ω=А АU V=А А∩0=0
Законы:
1. переместительный (коммутативный)
А+В=В+А
АВ=ВА
2. сочетательный (ассоциативный)
(А+В)+С=АВ+ВС
(АВ)С=А(ВС)
3. распределительный (дистрибутивный)
А(В+С)=АВ+АС
А+(ВС)=(А+В)(А+С)
События, наступающие, когда не наступает событиеА, называется противоположным событию А(или  ).
).

|
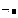 U=v
U=v 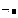 V=U
V=U 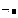
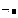 А=А А+
А=А А+ 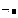 А=U
А=U
↓ТМП ↓ТМП ↓ТМП
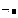 Ω=0
Ω=0 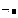 0=Ω А+
0=Ω А+ 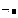 А=Ω
А=Ω
А 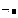 А=V
А=V
A∩ 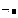 A=0
A=0
Правило де Моргана 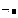 (А+В)=
(А+В)= 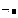 А+
А+ 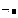 В
В
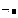 (АВ)=
(АВ)= 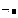 А+
А+ 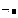 В
В
А и В – несовместные, если пересечение А и В=0 (А∩В=0)
Событие А1,А2,…,Аn образуют полную группу, если Uni=1Ai=Ω
Р(А) – вероятность события А
Событию А ставится в соответствие числу Р(А)
Аксиомы:
· вероятность А заключена между 0 и 1(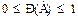 ) (1.7)
) (1.7)
· Р(V)=0, Р(U)=1 (1.8)
· Если А и В несовместные события(А∩В=0), то Р(А+В)=Р(А)+Р(В) (1.9)
Р(А)=  ωi?AР(ωi) (1.10)
ωi?AР(ωi) (1.10)

 На основании (1.8) получим Р(Uni=1ωi)=P(Ω)=1
На основании (1.8) получим Р(Uni=1ωi)=P(Ω)=1

 На основании (1.9) получим Р(Uni=1ωi)=
На основании (1.9) получим Р(Uni=1ωi)=  ni=1P(ωi)
ni=1P(ωi)
 ni=1P(ωi)=1
ni=1P(ωi)=1
Тогда все элементы события равновозможные.
Р(ω1)= Р(ω2)=…= Р(ωn)=1/n
|A|=m(А)
Мощность множества А – числоточек, входящих в А
Подставим в (1.10) |A|=m(А):
Р(А)= m(А)/n
Пространство элементарных событий Ω с заданным на нем распределением вероятности называется вероятностным пространством.
Вопрос 3.
Правило сложения.
1. для несовместных событий вероятность суммы 2 несовместных событий равна сумме вероятностей этих событий.
А∩В=0, i≠j→Р(Σni=1Ai)= Σni=1P(A)
Следствия:
· если событие А1, А2,…,Аn несовместны и образуют полную группу, то их сумма вероятностей равна 1.
Аi∩Aj=0, i≠j, Uni=1Ai=Ω→Σni=1P(Ai)=1
· сумма вероятностей противоположных событий равна 1
Р(А)+Р(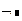 А)=1
А)=1
Р(А)=1-Р(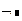 А)
А)
А={ω2,ω3,ω4}
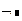 A={ω1} – вероятность появления хотя бы 1 герба Р(А)=1 – Р{ЦЦ}
A={ω1} – вероятность появления хотя бы 1 герба Р(А)=1 – Р{ЦЦ}
2.  для совместных событий
для совместных событий

|
|
|
 В=
В=
 С=
С=
Р(А+В)= Σωi?AUBP(ωi)= Σωj?AР(ωi)+ Σωk?B-Σωl?ABP(ωl)=Р(А)+Р(В)+Р(АВ)
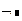 (А1+А2+…+Аn)=
(А1+А2+…+Аn)= 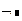 А1∙
А1∙ 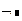 А2∙…∙
А2∙…∙ 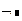 Аn
Аn
То в соответствии со следствием 2:
Р(А1+А2+…+Аn)=1-Р(А1+А2+…+Аn)=1-P(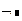 A1∙…∙
A1∙…∙ 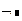 An)
An)
Вопрос 4.