Р(А|В)=Р(А),
т.е. условная вероятность совпадает с безусловной.
Для произведения независимых событий А и В получаем равенство
Р(АВ)=Р(А|В)Р(В)=Р(А)Р(В),
которое озвучивается так: вероятность произведения двух независимых событий равна произведению их вероятностей. Это равенство может быть также использовано в качестве определения независимости случайных событий.
Если А не зависит от В, т.е. Р(А|В)= Р(А), тогда и В не зависит от А, что доказывается цепочкой простых преобразований
Р(В|А) = 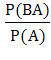 =
= 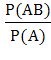 =
=  =
= 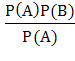 = Р(В).
= Р(В).
Примеры независимости случайных событий дают эксперименты с бросанием кубика или монеты, в которых одни и те же события в прошлом и будущем происходят с одной и той же вероятностью (Р(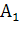 =”утром выпал орел”)= Р(
=”утром выпал орел”)= Р(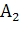 =”вечером выпал орел”)= Р(
=”вечером выпал орел”)= Р(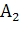 |
| 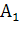 )=
)= 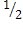 ).
).
Рассмотренную выше парную независимость случайных событий следует отличать от независимости в совокупности. Случайные события называются независимыми в совокупности, если они попарно независимы и каждое из них не зависит от произведения любого набора из остальных событий. В случае независимости событий в совокупности вероятность их произведения равна произведению вероятностей:
Р(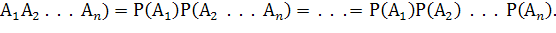
Пример. Стрелок попадает в мишень с вероятностью 0,6. Какова вероятность хотя бы одного попадания в серии из трех выстрелов?
Обозначим 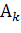 - попадание в мишень при 𝑘-й попытке. Поскольку попадание и промах образуют полный набор событий, то промах -
- попадание в мишень при 𝑘-й попытке. Поскольку попадание и промах образуют полный набор событий, то промах - 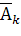 имеет вероятность Р(
имеет вероятность Р(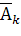 ) = 1-
) = 1- 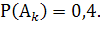 Событие А = “хотя бы одно попадание” противоположно событию В = “три промаха”, которое в принятой системе обозначений представляется в виде В=
Событие А = “хотя бы одно попадание” противоположно событию В = “три промаха”, которое в принятой системе обозначений представляется в виде В= 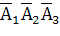 , т.е. А=
, т.е. А= 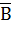 и тогда А + В = Ω. Далее, промахи
и тогда А + В = Ω. Далее, промахи 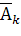 независимы в совокупности, поскольку в соответствии с условиями задачи их вероятность постоянна (не зависит от промахов в других выстрелах). Эти факты в совокупности позволяют вычислить искомую вероятность события следующим образом:
независимы в совокупности, поскольку в соответствии с условиями задачи их вероятность постоянна (не зависит от промахов в других выстрелах). Эти факты в совокупности позволяют вычислить искомую вероятность события следующим образом:
Р(А) = 1- Р(В) = 1- 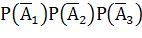 = 1-
= 1-  = 0,936.
= 0,936.
Следует отметить, что проверить решение данной задачи с помощью числовой таблицы не позволяет то обстоятельство, что попадания и промахи не равновозможны. Этот пример развеивает иллюзию всесильности прямого применения вычислительной схемы классической вероятности и свидетельствует, что ее возможности ограничены лишь самыми простыми случаями.
10 Формула полной вероятности
Теорема. Пусть случайные события  попарнонесовместны и событие А содержится в их сумме А Ì
попарнонесовместны и событие А содержится в их сумме А Ì 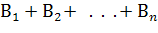 , тогда справедлива формула полной вероятности
, тогда справедлива формула полной вероятности
Р(А)= 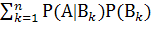 .
.
Доказательство. В условиях данной теоремы событие А можно представить в виде
А=А(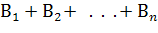 ) или А=
) или А= 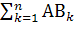 .
.
В силу попарной несовместности событий 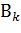
 =∅ при
=∅ при 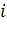 ≠
≠ 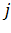 ) имеет место попарная несовместность событий А
) имеет место попарная несовместность событий А 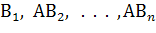 , поскольку
, поскольку 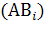 (А
(А 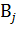 )=(А
)=(А 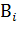 )(
)(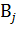 А)=А
А)=А 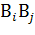 А=А(
А=А(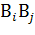 )А=А∅А=∅. Учитывая, что Р(
)А=А∅А=∅. Учитывая, что Р(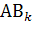 )=Р(
)=Р(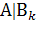 )Р(
)Р(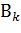 ) окончательно находим
) окончательно находим
Р(А)=Р(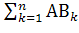 )=
)=  .
.
События  интерпретируются как условия наступления события А и называются предпосылками события А. События предпосылки принято называть гипотезами. Их вероятности известны до опыта и потому называются априорными. Теперь формулу полной вероятности можно трактовать следующим образом: вероятность любого события разлагается в сумму вероятностей гипотез, взятых с коэффициентами равными условным вероятностям данного события относительно этих гипотез. Иными словами, вероятности гипотез для всех остальных событий играют роль аналогичную базисным векторам в векторном пространстве.
интерпретируются как условия наступления события А и называются предпосылками события А. События предпосылки принято называть гипотезами. Их вероятности известны до опыта и потому называются априорными. Теперь формулу полной вероятности можно трактовать следующим образом: вероятность любого события разлагается в сумму вероятностей гипотез, взятых с коэффициентами равными условным вероятностям данного события относительно этих гипотез. Иными словами, вероятности гипотез для всех остальных событий играют роль аналогичную базисным векторам в векторном пространстве.
При решении задач для обеспечения условий применения формулы полной вероятности предпосылки 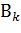 выбирают попарно несовместными и образующими полный набор, т.е.
выбирают попарно несовместными и образующими полный набор, т.е. 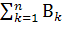 =Ω.
=Ω.
Пример. В первой группе из 20 студентов 5 юношей, а во второй группе из 30 студентов - 3 юноши. Какова вероятность того, что выбранный наугад студент - юноша (событие А)?
Поскольку выбранный студент числится в какой-либо из двух групп, то в качестве гипотез естественно принять его принадлежность первой группе - 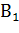 и второй группе -
и второй группе - 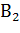 .Вероятности гипотез найдем исходя из доли численности групп в общем количестве студентов:
.Вероятности гипотез найдем исходя из доли численности групп в общем количестве студентов:
Р(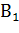 )=
)= 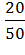 =
= 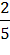 , Р(
, Р(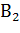 )=
)= 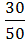 =
= 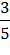 .
.
Затем найдем соответствующие условные вероятности, на сей раз исходя из доли юношей в каждой группе
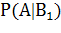 =
= 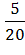 =
= 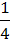 ,
, 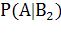 =
= 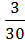 =
= 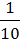 .
.
И, наконец, вычисляем окончательный результат
Р(А)= 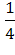 ·
· 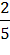 +
+ 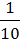 ·
· 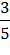 =
= 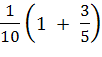 =
= 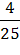 .
.
Простота задачи позволяет проконтролировать полученное решение, с помощью классической схемы. Поскольку выбор производится из совокупности в количестве 50 студентов при наличии в ней 8 юношей, то в соответствии с правилом классической вероятности
Р(А) = 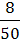 =
= 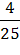 ,
,
чего и следовало ожидать.
При расчете вероятности сложных событий с использованием формулы полной вероятности схему решения задачи удобно анализировать, систематизировать и иллюстрировать с помощью, так называемого дерева вероятностей (дерева решений), ветви которого описывают развитие начальной ситуации по всем мыслимым сценариям. Для рассмотренной задачи дерево вероятностей будет иметь структуру, изображенную ниже.
| Выбрана группа |
Первая  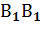
|
Вторая 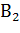
|
| Выбран студент |
| Выбран студент |
Р(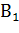 )= )= 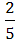
|
Р(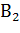 )= )= 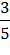
|
| юноша |
| юноша |
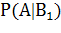 = = 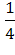
|
 = = 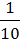
|
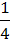 · · 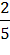 = = 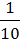
|
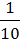 · · 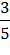 = = 
|
Р(А) = 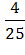
|
11 Формула Байеса
Для событий с предпосылками интересна и такая постановка вопроса: а какова вероятность предпосылки 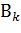 , если произошло событие А? Чтобы проиллюстрировать данную ситуацию с помощью рассмотренного выше примера переформулируем его следующим образом: найти вероятность того, что выбранный наугад студент учится в первой (или второй) группе, если известно что он - юноша.
, если произошло событие А? Чтобы проиллюстрировать данную ситуацию с помощью рассмотренного выше примера переформулируем его следующим образом: найти вероятность того, что выбранный наугад студент учится в первой (или второй) группе, если известно что он - юноша.
В этой и подобной ей задачах по сути дела требуется найти условную вероятность гипотезы 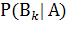 . Эту вероятность называют апостериорной в отличие от априорной вероятности
. Эту вероятность называют апостериорной в отличие от априорной вероятности  . Апостериорную вероятность находят при условии, что событие А уже произошло, т.е. после опыта. Решению этой задачи служит формула Байеса.
. Апостериорную вероятность находят при условии, что событие А уже произошло, т.е. после опыта. Решению этой задачи служит формула Байеса.
Теорема. Пусть случайные события  попарнонесовместны и событие А содержится в их сумме А Ì
попарнонесовместны и событие А содержится в их сумме А Ì 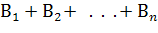 , тогда справедлива формула Байеса
, тогда справедлива формула Байеса
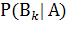 =
= 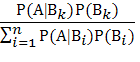 , 𝑘=1,2,..., n.
, 𝑘=1,2,..., n.
Доказательство этой теоремы осуществляется с помощью цепочки простых преобразований с использованием свойства коммутативности произведения событий, определения условной вероятности и формулы полной вероятности:
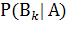 =
= 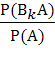 =
=  =
=  =
= 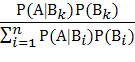 .
.
Теперь можно приступить к решению задачи, сформулированной в начале параграфа.
Итак, требуется найти 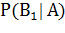 , где событие А=”выбран юноша”. Подставляем в формулу Байеса фигурирующие в ней вероятности, рассчитанные в предыдущем параграфе, и находим нужный ответ:
, где событие А=”выбран юноша”. Подставляем в формулу Байеса фигурирующие в ней вероятности, рассчитанные в предыдущем параграфе, и находим нужный ответ:
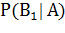 =
= 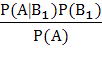 =
= 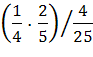 =
= 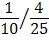 =
= 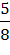 .
.
Решение задачи с помощью простой схемы классической вероятности не представляется возможным, что свидетельствует о ее применимости в самых несложных ситуациях.
ПРАКТИКУМ
Приведем сводку используемых формул:
Р(А+В)=Р(А)+Р(В) для несовместных событий А и В;
Р(А+В)=Р(А)+Р(В)+Р(АВ) для совместных событий А и В;
Р(АВ)=Р(А)Р(В) для независимых событий А и В;
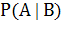 или
или 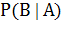 в случае зависимости событий А и В.
в случае зависимости событий А и В.
Операции над событиями
1. При стрельбе по мишени двух стрелков: А=”попадание в мишень перового стрелка”, В=”попадание в мишень второго стрелка”. Сумма этих событий по определению означает: в мишень попал либо первый стрелок, либо второй стрелок, либо они попали в мишень вместе (одновременно). Иными словами А+В=”попадание в мишень хотя бы одного стрелка”. Эта задача содержательно идентична серии из двух выстрелов одного стрелка. Обозначив А=”попадание в мишень в первом выстреле”, В=”попадание в мишень во втором выстреле” получим А+В=”хотя бы одно попадание в мишень в серии из двух выстрелов”.
Произведение событий в первом и втором случаях дает соответственно АВ=”попадание обоих стрелков” или АВ=”два попадания в серии из двух выстрелов” (“попасть дважды”).
2. При извлечении двух шаров из урны в случае  =”В ‘к’ попытке извлечен белый шар” сумма событий
=”В ‘к’ попытке извлечен белый шар” сумма событий 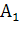 +
+ 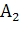 =”из двух извлеченных из урны шаров хотя бы один - белый ”. Извлечению двух белых шаров отвечает произведение АВ.
=”из двух извлеченных из урны шаров хотя бы один - белый ”. Извлечению двух белых шаров отвечает произведение АВ.
3. В обоих примерах, будь то стрельба или извлечение шаров из урны, не оговаривается необходимость физически одновременного осуществления испытаний - двух выстрелов или извлечения сразу двух шаров. Тем не менее, произведение событий трактуется как их одновременная реализация, понимаемая как осуществление и одного и другого события вместе. Отсюда сразу же протягивается ниточка к понятию совместности событий как возможности их реализации одновременно - в смысле вместе.
Ясное дело, что в рассмотренных примерах события А и В являются совместными, поскольку можно дважды попасть в мишень или извлечь два белых шара, если по условию задачи они в урне имеются.
Расчет числа исходов
Расчет количества возможных исходов базируется на основе содержательного анализа постановки решаемой задачи.
1. Определить количество способов упорядочения 8 различных объектов.
Поскольку объекты различны, то можно их рассматривать как условно перенумерованные. По условию задачи требуется определить число комбинаций из 8 цифр, отличающиеся не только самими цифрами, но и их порядком.
На первое место в комбинации может быть поставлена любая из 8 цифр, на второе любая из 7 оставшихся и при этом любой из 8 способов выбора первой цифры может комбинировать с любым из 7 способов выбора второй цифры и т.д. В итоге получаем внушительное число
N = 8! = 8·7·6·5·4·3·2·1 = 40320.
2. Готовится к выпуску лотерея с шестизначными номерами и трехзначными сериями. Сколько будет билетов всего, если в серии допускаются любые комбинации цифр (в том числе 000, 001 и т.п.) и в каждой серии предусматриваются всевозможные номера?
В серии насчитывается 3 цифры и серия 013 отличается от 103. При наборе серии на первое место может быть поставлена любая цифра из 10, на второе - любая опять-таки из 10 и т.д. Поскольку первая цифра может сочетаться с любыми комбинациями двух последующих цифр, то для числа серий получаем величину 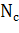 =10·10·10 =
=10·10·10 = 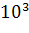 .
.
По тем же соображениям количество номеров в серии 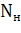 =
=  . По условию задачи столько билетов в каждой серии и потому всего билетов будет
. По условию задачи столько билетов в каждой серии и потому всего билетов будет 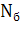 =
= 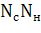 =
= 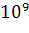 = 1 млрд, т.е. каждому жителю нашей страны достанется примерно 7 билетов.
= 1 млрд, т.е. каждому жителю нашей страны достанется примерно 7 билетов.
3. По доброте душевной преподаватель из 20 билетов разрешает студенту вытащить сразу 2. Сколькими различными способами это можно сделать?
Из самой постановки задачи абсолютно ясно, что студенту совершенно не важно, какую комбинацию номеров он вытащил (3, 7) или (7, 3) - для него данные комбинации неразличимы, а значение имеет лишь его способность ответить на эти билеты. Это значит, что ответ на поставленный вопрос следует искать с помощью числа сочетаний
N =  =
=  =
= 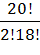 =
= 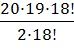 = 190.
= 190.
4. Сколькими способами можно распределить 6 различных книг между 3-мя студентами?
Сначала проанализируем постановку задачи. Очевидно, что для студента комбинации предметов (химия, философия) и (философия, химия) - неразличимы, т.е. комбинации должны отличаться только составом. Следовательно, при решении задачи следует задействовать число сочетаний. Чтобы установить вид формулы расчета достаточно составить схему дележа парами: первые два произвольно выбранные учебника отдать первому студенту (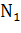 =
=  ), вторые два - второму (
), вторые два - второму (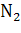 =
= 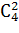 ), а на долю последнего студента придется оставшаяся пара (
), а на долю последнего студента придется оставшаяся пара (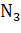 =
= 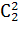 = 1). Поскольку каждый набор учебников первого студента может комбинировать со всеми наборами для двух других студентов, то эти числа должны быть взяты в произведении и ответом задачи является
= 1). Поскольку каждый набор учебников первого студента может комбинировать со всеми наборами для двух других студентов, то эти числа должны быть взяты в произведении и ответом задачи является
N = 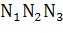 =
= 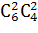 =
= 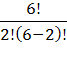
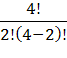 =
=  = 90.
= 90.
Однако дележ может быть устроен иначе - по одному учебнику каждому студенту по принципу “тебе-тебе-тебе” в два круга. В соответствии с такой схемой подсчет количества возможных вариантов дележа с учетом сокращения на каждом последующем шаге числа шаров на 1 будет производиться по формуле
N= 6·5·4·3·2·1 = 720.
Этот число существенно превышает верный результат, поскольку последняя схема не учитывает парный характер распределения книг и неразличимость комбинаций одного состава.
Таким образом, во избежание ошибок на передний план выдвигается содержательный анализ постановки задачи и построение на его основе алгоритма ее решения.
5. Определить вероятность ничьей в турнире из 4-х встреч двух равносильных игроков (команд), если ничьи в отдельной встрече не допускаются (пенальти, буллит и т.п.).
| 1 1 1 1 | 0 0 1 1 | 0 0 0 1 |
| 0 1 1 1 | 0 1 0 1 | 0 0 1 0 |
| 1 0 1 1 | 0 1 1 0 | 0 1 0 0 |
| 1 1 0 1 | 1 0 0 1 | 1 0 0 0 |
| 1 1 1 0 | 1 0 1 0 | 0 0 0 0 |
| 1 1 0 0 |
Поскольку противники равносильные, количество встреч четно и каждая из них может закончиться только победой или поражением, то внутренний голос достаточно уверенно нашептывает про ½ или 50%. Чтобы доказать правильность этого интуитивного ответа или опровергнуть его перечислим все мыслимые исходы матча и отберем среди них благоприятные. Заметим, что достаточно рассматривать итоги встреч с позиции только одного игрока, т.к. его победа означает поражение противника и наоборот. Возьмем одного игрока, условно называемого первым, и опишем его победу цифрой “1”, а поражение - ”0”. Знаки в кавычках могут рассматриваться как числа или символы. Теперь можно составить таблицу с перечислением всех исходов тур- нира. Первая строка первого столбца таблицы отвечает наиболее желаемому исходу турнира первого игрока - его победе во всех 4-х встречах. Далее в первом столбце идут игры с одним поражением в первой, второй и т. д. встречах. Второй столбец описывает игры с ничьей по итогам всех 4-х встреч. В трех первых строках последнего столбца обозначена только одна победа и в его последней строке стоит сокрушительный сухой разгром первого игрока. Всего в таблице 16 равновозможных и несовместных исходов, среди которых 6 благоприятных для ничьей по итогам турнира. Теперь, сле- дуя правилу вычисления классической вероятности, найдем вероят-
ность ничьей Р(“ничья”)= 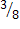 , т.е. свести вничью турнир с четным числом встреч двум равносильным противникам менее вероятно нежели выиграть или проиграть. Полученный результат изначально вовсе не очевиден и свидетельствует, что интуиция нас изрядно подвела, поскольку относительная ошибка составила (
, т.е. свести вничью турнир с четным числом встреч двум равносильным противникам менее вероятно нежели выиграть или проиграть. Полученный результат изначально вовсе не очевиден и свидетельствует, что интуиция нас изрядно подвела, поскольку относительная ошибка составила (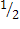 -
- 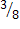 )/
)/ 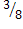 =
= 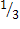 = 33,3%.
= 33,3%.
При наличии такой таблицы нетрудно рассчитать вероятности других возможных результатов матча. Например:
Р(“выиграть”)= 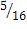 =Р(“проиграть”),
=Р(“проиграть”),
Р(“не проиграть”)= 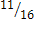 =Р(“не выиг рать ”),
=Р(“не выиг рать ”),
Р(“выиграть всухую”)= 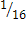 = Р(“проиграть всухую”),
= Р(“проиграть всухую”),
Р(“выиграть хотя бы один раз”)= 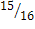 =Р(“проиграть хотя бы один раз”).
=Р(“проиграть хотя бы один раз”).
Здесь наблюдается своеобразная симметрия рассмотренных событий. Уместно отметить также, что противоположным к “выиграть” является не “проиграть”, а “не выиг рать ”. Сумма именно этих событий является достоверным событием, а сумма их вероятностей равна 1.
Задача. Стрелок попадает в мишень с вероятностью 0,5. Каковы вероятности попадания дважды и хотя бы одного попадания в серии из двух выстрелов? Решить задачу по формулам и проверить полученные результаты с помощью числовой таблицы с перечислением всех мыслимых исходов.
Подсказка: решение основывается на взаимоотношении событий в плане их совместности - несовместности и зависимости - независимости.
Ограниченность возможностей простой схемы классической вероятности демонстрирует следующий более мудреный пример.
Задача. В первой урне находится 1 белый и 9 черных шаров, а во второй - 5 белых и 1 черный. Из каждой урны наугад вынули по одному шару, а остальные ссыпали в третью урну, из которой извлекли один шар. Найти вероятность того, что:
- из третьей урны вынут белый шар;
- из обеих урн вынули белые шары, если из третьей урны извлекли
белый шар.
Сообразно постановке задачи введем обозначения событий, фигурирующих в ней непосредственно, а также событий, отвечающих всевозможным сценариям объединения урн: А=”из третьей урны извлечен белый шар”;  и
и 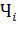 - из 𝑖-й урны (𝑖=1,2) извлечены соответственно белый и черный шар. Теперь следуя логике решения первой части задачи, изобразим дерево вероятностей с учетом всех возможных исходов при проведении трех шагового мысленного эксперимента: вынули шар из первой урны, вынули шар из второй урны, вынули шар из третьей урны. Этим опытам будет отвечать трехуровневое дерево вероятностей.
- из 𝑖-й урны (𝑖=1,2) извлечены соответственно белый и черный шар. Теперь следуя логике решения первой части задачи, изобразим дерево вероятностей с учетом всех возможных исходов при проведении трех шагового мысленного эксперимента: вынули шар из первой урны, вынули шар из второй урны, вынули шар из третьей урны. Этим опытам будет отвечать трехуровневое дерево вероятностей.
| Из У1 вынут |
Р(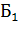 )= )= 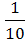
|
Р(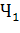 )= )= 
|
| Белый шар |
| Из У2 вынут |
| Черный шар |
| Из У2 вынут |
Р(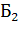 )= )= 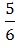
|
Р(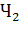 )= )= 
|
| Белый шар |
| Из У3 вынут |
| Черный шар |
| Из У3 вынут |
| Белый шар |
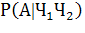 = = 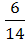
|
| Белый шар |
 = = 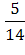
|
Р(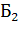 )= )= 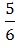
|
Р(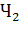 )= )= 
|
| Белый шар |
| Из У3 вынут |
| Черный шар |
| Из У3 вынут |
| Белый шар |
 = = 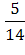
|
| Белый шар |
 = = 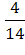
|
В этой схеме итоговые условные вероятности посчитаны исходя из наличного количества белых и черных шаров, соответствующего развитию начальной ситуации по тому или иному сценарию.
В качестве гипотез примем всевозможные комбинации выбора шаров: 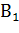 =
=  (из обеих урн вынули по белому шару),
(из обеих урн вынули по белому шару), 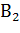 =
= 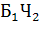 (из первой - белый из второй - черный),
(из первой - белый из второй - черный), 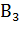 =
= 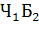 ,
, 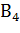 =
= 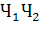 . Эти гипотезы
. Эти гипотезы
сформированы как произведения независимых событий и сами являются независимыми и попарно несовместными событиями, образующими полный набор, т.е. непременно происходит одно из 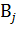 , 𝑗=1, 2, 3, 4 и А содержится в их сумме. Таким образом, удовлетворены условия применимости формулы полной вероятности и
, 𝑗=1, 2, 3, 4 и А содержится в их сумме. Таким образом, удовлетворены условия применимости формулы полной вероятности и
Р(А) = 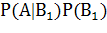 +
+ 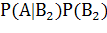 +
+ 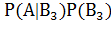 +
+ 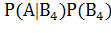 .
.
В силу независимости событий 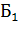 и
и 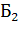 ,
, 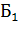 и
и 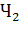 ,
, 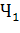 и
и 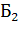 ,
, 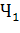 и
и 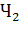 имеем
имеем
Р(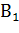 )= Р(
)= Р(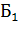 )Р(
)Р(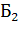 ), Р(
), Р(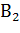 )= Р(
)= Р(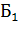 )Р(
)Р(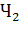 ), Р(
), Р(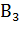 )= Р(
)= Р(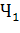 )Р(
)Р(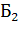 ), Р(
), Р(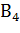 )= Р(
)= Р(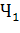 )Р(
)Р(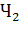 ).
).
Подставляя сюда численные значения нашей задачи, получаем
Р(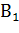 )=
)=  =
= 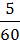 , Р(
, Р(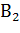 )=
)=  =
= 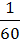 , Р(
, Р(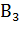 )=
)= 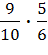 =
= 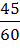 , Р(
, Р(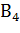 )=
)= 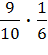 =
= 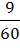 ,
,
и, взяв с дерева вероятностей значения условных вероятностей, окончательно находим решение первой части задачи
Р(А) = 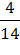 ·
· 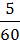 +
+ 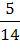 ·
· 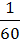 +
+ 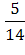 ·
· 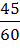 +
+ 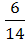 ·
· 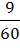 =
= 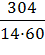 =
= 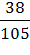 ≈ 0.36 = 36%.
≈ 0.36 = 36%.
Ответ на вторую часть задачи (вероятность гипотезы 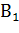 ) дает формула Байеса
) дает формула Байеса
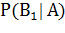 =
= 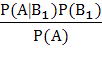 =
=  =
= 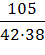 =
= 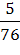 .
.
Задача. В первой урне 7 белых и 9 черных шаров, во второй - 6 белых и 4 черных. Из первой урны извлекли 2 шара, переложили во вторую урну, все в ней перемешали и наугад достали 1 шар. Какова вероятность того, что этот шар белый (событие В).