В теории и практике систем автоматического управления наибольшее применение находят амплитудно-фазовые частотные характеристики (АФХ или их иногда называют годографами Найквиста), логарифмические частотные характеристики (диаграммы Боде) и амплитудные частотные характеристики. Для их расчета и построения в Control System Toolbox включены соответствующие функции.
Построение частотного годографа Найквиста осуществляется с помощью группы функций nyquist:
nyquist(sys),
nyquist(sys,dw),
где sys – непрерывная или дискретная lti- модель любого подкласса;
dw={Wmin, Wmax} – диапазон частот;
Wmin, Wmax – соответственно минимальная и максимальная частоты.
Частотный диапазон можно также задать с помощью массива конкретных частот dw=[w1,w2,…,wn], где n – число частот.
Для создания логарифмически распределенного вектора частот используется команда logspaсe. Эта функция возвращает вектор-строку логарифмически возрастающих частот:
logspaсe(log10(Wmin), log10(Wmax))
logspaсe(log10(Wmin), log10(Wmax), N),
где N – число точек в диапазоне частот (по умолчанию N =50).
Основной функцией является nyquist(sys), в которой частотный диапазон определяется автоматически по минимальному и максимальному значениям и массива нулей и полюсов lti -модели. Если последняя содержит астатизм, то выдается предупреждающее сообщение, что на нулевой частоте характеристика равна бесконечности (неопределенное значение). Поэтому в этом случае целесообразно использовать функцию вида nyquist(sys,dw). В практических задачах функция nyquist наиболее часто применяется для построения годографа разомкнутой САУ с целью исследования устойчивости замкнутой системы с помощью критерия Найквиста.
Для дискретных систем из-за периодичности частотной характеристики АФХ рассчитывается в диапазоне от нуля до частоты Найквиста ( ). Если период Ts неспецифицирован, то по умолчанию принимается Ts = 1.
). Если период Ts неспецифицирован, то по умолчанию принимается Ts = 1.
Пример 2.8. Построение АФХ разомкнутой системы с ПФ W(s) (рис.2.2).
>> nyquist(w)

Рис. 2.2. Амплитудно-фазовая характеристика разомкнутой системы
Задание 2.8.Постройте годограф Найквиста дискретной САУ по ПФ разомкнутой системы D(z).
Если требуется построить годографы Найквиста для нескольких систем в одних координатах, то можно использовать функцию nyquist в более общих формах:
nyquist(sys1, sys2,…,sysN)
nyquist(sys1, sys2,…,sysN, dw)
nyquist(sys1, 'plotstyle1',…,sysN, 'plotstyleN'),
где 'plotstyleK' – аргумент, определяющий стиль линии, т.е. цвет и тип годографа K -ой lti -модели.
Примечание. Задание стиля осуществляется в соответствии с правилами оформления графиков в MATLAB – в виде набора трех символьных маркеров, заключенных в апострофы. Один из них определяет тип линии (табл. 2.1), другой – цвет (табл. 2.2). При этом можно указывать не все маркеры. В этом случае действуют маркеры, установленные по умолчанию. Порядок маркеров в строке стиля не регламентирован, т.е. может быть произвольным.
Таблица 2.1
Тип линии
| Маркер | Тип линии |
| – | непрерывная |
| - - | штриховая |
| : | пунктирная |
| –. | штрихпунктирная |
Таблица 2.2
Цвет линии
| Маркер | Цвет линии |
| c | голубой (cean) |
| m | фиолетовый (magenta) |
| y | желтый (yellow) |
| r | красный (red) |
| g | зеленый (green) |
| b | синий (blue) |
| w | белый (white) |
| k | черный (black) |
Пример 2.9. Построение АФХ разомкнутой системы соответственно с ПФ W(s) и 0.5W(s) в одних координатах комплексной плоскости с пометкой годографа W(s) маркером 'r-', а годографа 0.5W(s) - маркером ':b' (рис.2.3).
>> nyquist(w,'r-',0.5*w,':b')

Рис. 2.3. Маркированные годографы Найквиста
Задание 2.9.Постройте годографы Найквиста для разомкнутой дискретной системы с ПФ D(z) и 0.7D(z), пометив годограф D(z) маркером ‘-.g’, а годограф 0.7D(z) – маркером ‘m- -‘.
Имеются две формы вызова функции nyquist, которые применяются для расчета годографа Найквиста без его построения:
[re,im,w]= nyquist(sys)
[re,im,w]= nyquist(sys,dw)
где re,im – соответственно векторы значений вещественной и мнимой частей частотной передаточной функции; w – вектор вычисленных частот (при необходимости его можно опустить).
Пример 2.10. Расчет значений действительной и мнимой частотных характеристик разомкнутой системы с ПФ W(s) в частотном диапазоне 1 - 30 рад/с.
>> [Re,Im]= nyquist(w,logspace(log10(1),log10(30),5))
| Re(:,:,1) =-2.8548 Re(:,:,2) =-0.8272 Re(:,:,3) =-0.3703 Re(:,:,4) =-0.1267 Re(:,:,5) =0.0214 | Im(:,:,1) =-2.4108 Im(:,:,2) =-0.8645 Im(:,:,3) =-0.2049 Im(:,:,4) =0.0310 Im(:,:,5) =-0.0070 |
Задание 2.10. Вычислите значения параметров АФХ для разомкнутой дискретной системы с ПФ D(z) в диапазоне частот от 0 до π/Тs.
Построение логарифмических частотных характеристик (ЛЧХ) осуществляется с помощью функции bode, которая как и функция nyquist имеет несколько форм обращения:
bode(sys)
bode(sys,dw)
bode (sys1, sys2,…,sysN)
bode (sys1, sys2,…,sysN, dw)
bode (sys1, 'plotstyle1',…,sysN, 'plotstyleN')
[mag, phase, w]= bode(sys)
где sys – непрерывная или дискретная lti -модель; mag, phase, w – соответственно векторы амплитуд, фаз (в градусах) и частот (рад/с).
Все команды, кроме последней, осуществляют построение диаграмм Боде, представляющих совокупность двух частотных характеристик в логарифмическом масштабе: логарифмической амплитудно-частотной характеристики (ЛАЧХ) и логарифмической фазо-частотной характеристики (ЛФЧХ).
Пример 2.11. Построение логарифмических частотных характеристик для системы, заданной ПФ W(s) (рис.2.4), где команда grid on использована для нанесения сетки на график.
>> bode(w); grid on % Здесь команда grid on использована для % нанесения сетки на график

Рис. 2.4. Логарифмические частотные характеристики системы
Задание 2.11.Постройте диаграмму Боде для разомкнутой дискретной системы с ПФ D(z).
Использование других вариантов функции bode аналогично функции nyquist.
Пример 2.12. Расчет параметров ЛЧХ для разомкнутой системы с ПФ W(s).
>> [Mag12,Phase12,W]=bode(w,[0.5,1,4,8,17])
Mag12(:,:,1) = 12.7870
Mag12(:,:,2) = 3.7365
Mag12(:,:,3) = 0.6285
Mag12(:,:,4) = 0.2531
Mag12(:,:,5) = 0.0974
Phase12(:,:,1) = -146.7687
Phase12(:,:,2) = -139.8197
Phase12(:,:,3) = -141.4908
Phase12(:,:,4) = -167.2469
Phase12(:,:,5) = -214.7002
W = 0.5000
1.0000
4.0000
8.0000
17.0000
Задание 2.12. Постройте таблицу значений амплитуды и фазы от частоты для разомкнутой дискретной системы с ПФ D(z).
Очень часто требуется определять запасы устойчивости системы по амплитуде (модулю) и фазе. Из теории автоматического управления известно, что запас устойчивости по модулю равен значению амплитудной частотной характеристики (АЧХ) на частоте Wc, при которой фазовая частотная характеристика (ФЧХ) имеет значение -1800, а запас по фазе – значение разности между ФЧХ и - 1800 на частоте среза Wcр. Для определения этих параметров используется функция margin:
margin(sys)
[Gm, Pm, Wc, Wcp]= margin(sys)
Здесь sys – непрерывная или дискретная lti -модель;
Gm – запас по модулю на частоте Wc;
Pm – запас по фазе на частоте среза Wcp.
Команда margin(sys) строит диаграмму Боде с указанием запасов устойчивости, а функция [Gm, Pm, Wc, Wcp]=margin(sys) рассчитывает значения Gm, Pm, Wc и Wcp без построения логарифмических частотных характеристик.
Пример 2.13. Определение запасов устойчивости непрерывной системы с ПФ разомкнутой системы W(s) (рис. 2.5).
>> margin(w)
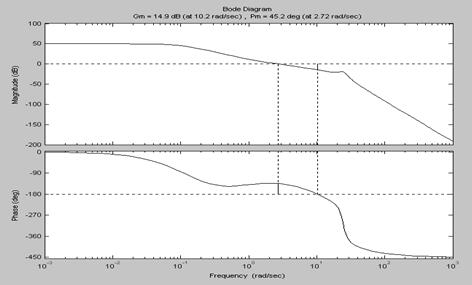
Рис. 2.5. Диаграмма Боде, построенная с помощью функций margin
Задание 2.13.Рассчитайте значения запасов устойчивости по модулю и фазе дискретной системы с ПФ разомкнутой системы D(z) без построения ЛЧХ.
При проектировании САУ часто используется показатель колебательности, который определяется в виде отношения максимального значения модуля частотной характеристики замкнутой системы к его величине на нулевой частоте (коэффициенту передачи системы).
Максимальное значение модуля частотной характеристики связано с нормой типа 
- для непрерывных систем соотношением

- для дискретных систем - соотношением

В связи с этим была составлена и включена в пакет Control System Toolbox функция norm в следующих формах:
normsys = norm(sys, inf)
normsys = norm(sys, inf, tol)
[ninf, fpeak]= norm(sys, inf),
где normsys – максимальное значение АЧХ lti-модели sys;
inf – идентификатор нормы  ;
;
tol – точность расчета нормы (по умолчанию tol =1е-2);
ninf - максимальное значение модуля частной характеристики на частоте fpeak.
При этом необходимо учитывать, что если объект sys имеет астатизм, то максимальное значение модуля АЧХ равно бесконечности.
Пример 2.14. Расчет максимального значения АЧХ динамической системы с ПФ замкнутой системы Ф(s).
>> [Am, Fm]=norm(f, inf)
Am =
13.7209
Fm =
1.7976
Задание 2.14. Определите значение показателя колебательности дискретной САУ с ПФ замкнутой системы Т(z), учитывая, что ее коэффициент передачи равен единице.