| PropertyName | PropertyValue |
| a b c d StateName | Матрица состояний Матрица входа Матрица выхода Матрица обхода Названия переменных состояния |
Для извлечения данных из созданных lti-моделей используются функции tfdata, zpkdata, ssdata в следующей форме:
[num, den, Ts] = tfdata (sys, 'v')
[z, p, k, Ts] = zpkdata (sys, 'v')
[a, b, c, d, Ts] = ssdata (sys),
где sys – модель любого подкласса lti.
При получении данных непрерывных моделей параметр Ts опускают. Параметр 'v' тоже можно опустить, но он улучшает форму представления num, den, z и p (вывод в виде векторов-строк). Указанные функции применимы к моделям sys любого подкласса. При этом автоматически осуществляется предварительное преобразование объекта sys в lti -модель, определяемую типом функции.
Пример 1.23. Вывод параметров tf -объекта на примере модели w22:
>> [num, den]=tfdata(w22, 'v')
num = 0 0 10
den = 0.0432 0.3600 1.0000
Задание 1.23. Проверьте параметры lti-модели для всех трех подклассов модели h22.
Более полную характеристику lti- моделей дает функция get:
Value=get(sys, 'PropertyName') % возвращает текущее
значение свойства
PropertyName
Struct= get(sys) % формирование
информации о структуре
lti-объекта в виде
массива записей
get(sys) % вывод свойств
lti-объекта и их текущих
значений.
На практике чаще применяется последний вариант вызова функции get.
Пример 1.24. Использование функции get для вывода свойств модели w22:
>> get(w22)
z: {1x1 cell}
p: {1x1 cell}
k: 10
Variable: 's'
DisplayFormat: 'roots'
Ts: 0
ioDelay: 0
InputDelay: 0
OutputDelay: 0
InputName: {''}
OutputName: {''}
InputGroup: {0x2 cell}
OutputGroup: {0x2 cell}
Notes: {}
UserData: []
Задание 1.24. Просмотрите параметры модели h22 с помощью функции get.
Для установки значений lti -объекта используются три способа:
· с помощью функций tf, zpk, ss (при создании одноименных lti -моделей);
· с помощью функции set;
· непосредственным присваиванием значений свойствам lti-модели.
Первый способ по существу расширяет список аргументов функций tf, zpk, ss парами 'Property Name', 'Property Value'.
Пример 1.25. Cоздание tf -модели по передаточной функции электродвигателя постоянного тока независимого возбуждения с передаточной функцией:
 ,
,
где U – напряжение питания (вход), N – скорость вращения электродвигателя (выход).
>> w25 =tf(2, [0.0432, 0.36, 1], 'inputname', 'U', 'outputname', 'N', 'notes', 'Электродвигатель','variable', 'p')
Transfer function from input "U" to output "N":
 2
2
0.0432 p^2 + 0.36 p + 1
Проверка свойств модели w25 с помощью функции get:
>> get(w25)
num: {[0 0 2]}
den: {[0.0432 0.36 1]}
Variable: 'p'
Ts: 0
ioDelay: 0
InputDelay: 0
OutputDelay: 0
InputName: {'U'}
OutputName: {'N'}
InputGroup: {0x2 cell}
OutputGroup: {0x2 cell}
Notes: {'Электродвигатель'}
UserData: []
Задание 1.25. Сформируйте ss-модель h25 следящего электропривода sys25 по его передаточной функции

с введением в модель следующих названий: BETA - входная координата, ALPHA – выходная координата, СЛЕДЯЩИЙ ЭП - название модели. Затем проверьте установку свойств с помощью функции struct = get (h25).
Второй способ установки значений lti -объекта заключается в изменении его отдельных свойств с помощью команды set:
set(sys, 'Property1', Value1, 'Property2', Value2,…),
где sys – идентификатор модели.
Пример 1.26. Изменение названия входа и выхода модели w25 соответственно на НАПРЯЖЕНИЕ и СКОРОСТЬ, а переменной p на s:
>>set(w25, 'inputname', 'НАПРЯЖЕНИЕ', 'outputname',
'СКОРОСТЬ', 'variable', 's')
Проверка с помощью функции get подтверждает правильность сделанных изменений:
>> get(w25)
num: {[0 0 2]}
den: {[0.0432 0.36 1]}
Variable: 's'
Ts: 0
ioDelay: 0
InputDelay: 0
OutputDelay: 0
InputName: {'НАПРЯЖЕНИЕ'}
OutputName: {'СКОРОСТЬ'}
InputGroup: {0x2 cell}
OutputGroup: {0x2 cell}
Notes: {'Электродвигатель'}
UserData: []
Задание 1.26. Измените название модели h25 на СЕРВОПРИВОД и введите запаздывание по входу τ=0,18 с. Извлеките информацию о новых свойствах модели.
Третий способ установки значений свойств lti -объекта связан с использованием операции присваивания полям модели требуемого значения:
sys.PropertyName = PropertyValue,
где sys.PropertyName – имя свойства модели sys;
PropertyValue – значение свойства.
Пример 1.27. Изменение названия модели w25 на ЭД и свойства num на значение 10:
>> w25.notes='ЭД'; w25.num=10
Transfer function from input "НАПРЯЖЕНИЕ" to output
"СКОРОСТЬ":
 10
10
0.0432 s^2 + 0.36 s + 1
Задание 1.27. Используя метод присваивания, установите в модели h25 значение запаздывания τ=0,2 с и измените название ее входной координаты на TETA. Проверьте сделанные изменения путем извлечения информации о свойствах модели.
Следует иметь ввиду, что переустановка значения периода квантования Ts в дискретной модели не изменяет ее параметры. Поэтому такая задача решается только с помощью функции d2d.
Пример 1.28. Установка в дискретной модели w17 нового значения периода дискретности Ts = 0,2 с помощью функции set:
>> w17.Ts = 0.2
Zero/pole/gain:
 0.038705 (z+0.6065)
0.038705 (z+0.6065)
(z-0.6065) (z-0.3679)
Sampling time: 0.2
Как видно из полученного результата коэффициенты модели не изменились, хотя период Ts установился. Для получения правильного результата необходимо применить функцию d2d:
>> w17. Ts = 0.25; % восстановление Ts
>> w17d = d2d (w17, 0.2)
Zero/pole/gain:
0.027172 (z+0.6703)
 (z-0.6703) (z-0.4493)
(z-0.6703) (z-0.4493)
Sampling time: 0.2
Полученные результаты говорят, что изменился и период квантования Ts и соответствующие ему коэффициенты модели.
Дополнительное упражнение
1. Построить lti -модели всех звеньев САУ, структурная схема которой приведена на рис.1.4, где kи =2,2; kп =0,8; с0 =0,9; k0 =10, Т01 =0,1с, Т02 =1с.
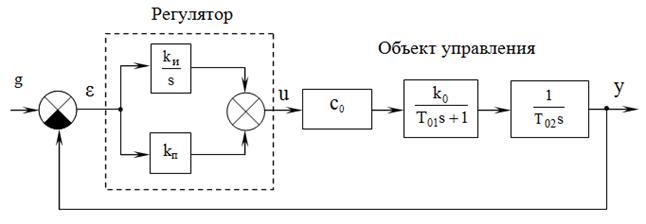
Рис. 1.4. Структурная схема САУ
2. Получить tf-, zpk- и ss -модели разомкнутой и замкнутой САУ.
3. Преобразовать непрерывную САУ в дискретную систему (рис. 1.5) с Тs =0,1с, переоборудовав регулятор с помощью аппроксимации Тастина в дискретное устройство управления с передаточной функцией D(z).
4. Сформировать дискретную модель непрерывной части системы W(z) (рис.1.5), где H0(s) – фиксатор нулевого порядка, W(s) – ПФ непрерывной части системы.

Рис. 1.5. Дискретная система управления
5. Изменить период квантования на Тs =0,05с и переопределить дискретные передаточные функции регулятора D(z) и непрерывной части системы W(z).
6. Получить lti -модель замкнутой дискретной системы.
7. Ввести в модель дискретной САУ наименования координат входа и выхода и название системы "СУЛ-3".
8. Проверьте все параметры и значения свойств полученной дискретной модели замкнутой САУ.
Контрольные вопросы
1. Какие подклассы lti -моделей используются в Control System Toolbox?
2. С помощью каких функций формируются lti -объекты?
3. Каким образом создать lti -модель статического звена?
4. Поясните особенности создания дискретных объектов.
5. Что такое dsp -форма дискретной tf -модели и как ее сформировать?
6. Как создать lti -модель с запаздыванием?
7. Какие функции используются для преобразования непрерывных моделей в эквивалентные дискретные lti -модели?
8. В чем отличие обычного преобразования Тастина от преобразования Тастина с коррекцией?
9. Как перейти от дискретной модели динамической системы к эквивалентной непрерывной lti -модели?
10. Поясните идею алгоритма, реализуемого в функции d2d?
11. Как осуществить переход от модели одного lti-подкласса к другому подклассу?
12. Какие правила предпочтения определяют получение результирующей модели?
13. Какие функции используются для определения результирующей модели при параллельном соединении двух lti -моделей?
14. Какие функции используются для определения результирующей модели схемы из двух последовательно соединенных lti -объектов?
15. Поясните особенности использования функции feedback для встречно-параллельного соединения lti -моделей.
16. Какие способы установки новых свойств lti -объекта Вы знаете?
17. Какие функции используются для извлечения данных из созданных lti-объектов?
18. Поясните особенности использования функции get.
2. АНАЛИЗ ЛИНЕЙНЫХ СТАЦИОНАРНЫХ СИСТЕМ С
ПОМОЩЬЮ ПАКЕТА CONTROL SYSTEM TOOLBOX
Для исследования стационарных линейных систем в пакете Control System Toolbox включены специальные функции, которые можно условно разделить на четыре группы:
· функции, предназначенные для анализа динамических параметров lti -моделей, таких как полюсы и нули, коэффициенты демпфирования, частоты собственных колебаний и другие;
· функции, предназначенные для расчета и построения временных характеристик, в частности, переходной, весовой и других переходных процессов;
· функции, предназначенные для расчета и построения различного вида частотных характеристик;
· функции, предназначенные для исследования свойств и оценки параметров динамических моделей в пространстве состояний.
Для изучения всех этих функций далее будет использоваться линейная САУ, имеющая передаточные функции разомкнутой W(s) и замкнутой Ф(s) систем следующего вида:


Соответствующие им lti -модели w и f можно сформировать с помощью функции tf:
>> w=tf([684.3 932.3 316.8], [0.002731 0.08829 2.467 47.05 277.2 133.8 20.65 1])
Transfer function:
 684.3 s^2 + 932.3 s + 316.8
684.3 s^2 + 932.3 s + 316.8
0.002731 s^7+0.08829 s^6+2.467 s^5 + 47.05 s^4 + 277.2 s^3 + 133.8 s^2 + 20.65 s +1
>> f=tf([21.53 29.34 9.969], [8.593e-6 2.778e-4 7.763e-3 0.148 0.8722 2.574 2.998 1])
Transfer function:
21.53 s^2 + 29.34 s + 9.969
8.593e-06s^7+0.0002778s^6+0.007763 s^5+0.148s^4+0.8722s^3+2.574 s^2+2.998s+1
Аналогично для выполнения текущих заданий предлагается использовать дискретную САУ с передаточной функцией разомкнутой системы D(z) следующего вида:

!! Сформируйте сначала tf-модель d по ПФ разомкнутой дискретной системы D(z) с периодом квантования Ts=0,05 с, а затем – tf-модель замкнутой дискретной системы T с единичной отрицательной обратной связью.