Практичсеское занятие 1.
1.1. Разработка вариантов стальной балочной клетки
1.1.1. Вариант 1. Балочная клетка нормального типа
Расчет настила
Сбор нагрузки на 1 м2 настила.
Таблица 1
| Наименование нагрузки | Нормативная нагрузка, кН/м2 | gf | Расчетная нагрузка, кН/м2 | |
| Временная нагрузка - Р | 1,2 | 14,4 | ||
| Собственный все настила gН = g´ tН = где удельный вес стали- g = r ´ g = 7850 ´ 9,81´ 10-3 | 0,924 | 1,05 | 0,97 | |
| Итого q = g +Р | qn = 12,924 | q = 15,37 |
Средняя величина коэффициента надежности по нагрузке
Примем расчетную схему настила (рис.4)
 |
Сварные швы крепления настила к балкам не дают возможности его опорам сближаться при изгибе. Поэтому в настиле возникают растягивающие цепные усилия Н. Изгиб настила происходит по цилиндрической поверхности. Цилиндрический модуль упругости стали определяется по формуле:
В расчете определим наибольший пролет полосы настила единичной ширины при заданной толщине листа tН = 0,012 м и предельном прогибе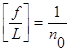 
:
После подстановки величин qn и tН в формулу, получаем:
 |
Принимаем L = 1,944 м, т.е. пролет LН укладывается 9 раз по длине главной балки. Предельный прогиб для заданного пролета
. Вычисляем наибольший пролет: Lmax = 2,12 м. По расчету принимаем LН = 1,944 м.
Разбивка главной балки показана на рис.5
Проверка прогиба настила.
Вычислим балочный прогиб, т.е. прогиб от поперечной нагрузки в середине полосы шириной b = 1 м, имеющий цилиндрическую жесткость Е1J, без учета растягивающей силы Н:
Прогиб настила с учетом растягивающей силы Н:
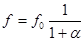, коэффициент a найдем по формулам.
Прогиб настила: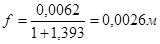 
Относительный прогиб: 
Предельный прогиб: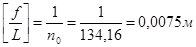 
- проверка удовлетворяется
Проверка прочности настила:
Изгибающий момент с учетом приварки настила на опорах:
Растягивающая сила
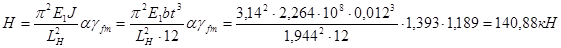
Проверка прочности полосы настила шириной b = 1 м.
,
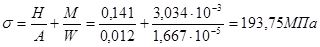где W=(t2Н)/6 =0,0122/6 = 2,4×10-5 м3
gСRg =1,1×230 = 253 МПа, где Rg =230 МПа - расчетное сопротивление проката по табл. 51* СНиП II-23-81*
s < gСRg - условие выполняется.
Расчет сварного шва крепления настила к балке.
1. Расчет по металлу шва
- коэффициент глубины провара шва bf = 0,7 (табл. 34* СНиП II-23-81*)
- коэффициент условия работы шва gwf = 1 (по п.11.2 СНиП II-23-81*)
В соответствии с табл. 55 СНиП II-23-81* принимаем электроды типа Э42. Расчетное сопротивление металла шва R wf = 180 МПа.
bf ×gwf × R wf = 0,7 × 1 × 180 = 126 МПа
2. Расчет по металлу границы сплавления.
- коэффициент глубины провара шва bz = 1,0 (табл.34 СНиП II-23-81*)
- коэффициент условия работы шва gwz = 1 (п.11.2* СНиП II-23-81*)
Расчетное сопротивление по металлу границы сплавления:
R wz = 0,45 Run = 0,45 × 360 = 162 МПа (по табл. 3 СНиП II-23-81*),
где Run - нормативное сопротивление фасонного проката.
bz× gwz × R wz = 1×1×162 = 162 МПа
Минимальная из величин при расчетах по металлу шва и по металлу границы сплавления (b× gw × R w)min = 126 МПа
Требуемый катет шва
Принимаем Кf = Кfmin = 5 мм
Расчет балки настила
Балку рассчитываем как свободно опертую, загруженную равномерной нагрузкой. Пролет равен шагу главных балок 7 м.
Погонную нагрузку собираем с полосы шириной, равной пролету настила LН = 1,944 м.
а) нормативная нагрузка:
qHб = qn LH + gHб = qn LH + 0,02 qn LH = 12,924 × 1,944 + 0,02 × 12,924 × 1,944 = 25,63 кН/м, где в первом приближении вес балки принимаем равным 2% от нагрузки.
б) расчетная нагрузка:
qб = q LH + gHбgf = 15,37 × 1,944 + 0,502 × 1,05 = 30,41 кН/м
Изгибающий момент от расчетной нагрузки
Требуемый момент сопротивления
,
где с1 = 1,1 - коэффициент, учитывающий развитие пластических деформаций в первом приближении.
Требуемый момент инерции по предельному прогибу (при Lбн = 7 м n0 = 202,78)
Принимаем двутавр №40Б1 ГОСТ 26020-83 (Jх = 15 750 см4, Wх = 803,6 см3, А = 61,25 см2, bf = 165 мм, tf = 10,5 мм, tw = 7,0 мм, h = 39,2 см, масса mбн = 48,1 кг/м)
Уточним коэффициент с1:
площадь сечения стенки Аw = tw (h- 2tf) = 0,7(39,2 - 2 × 1,05) = 25,97 см2
площадь сечения полки Аf = (A - Aw) × 0,5 = (61,25 - 25,97) × 0,5 = 17,64 см2
По табл. 66 СНиП II-23-81* коэффициент с = 1,091. Принимаем с1 = с.
Уточним собственный вес балки и всю нагрузку
а) нормативная
qHб = qn LH + mбн g = 12,924 × 1,944 + 48,1 × 9,81 × 10-3 = 25,60 кН/м
б) расчетная
qб = q LH + mбн ggf = 15,37 × 1,944 + 48,1 × 9,81 × 10-3 × 1,05 = 30,37 кН/м
Максимальный изгибающий момент
Проверка нормальных напряжений
Условие прочности удовлетворяется с недонапряжением (253-212,17)×100%/ 253 = 16,1 %.
Расчетная перерезывающая сила на опоре
Qmax = qб L/2 = 30,37 × 7 × 0,5 = 106,3 кН
Проверка касательных напряжений на опоре
,
где hw = h - 2tf = 39,2 - 2 × 1,05 = 37,1 см
t = 40,51 МПа < RS gS = 0,58 × 230 × 1,1 = 146,7 МПа
Условие прочности выполняется с большим запасом
Проверка прогиба балки
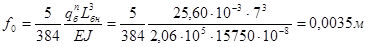
-проверка выполняется
Высота покрытия по главным балкам определяется как высота балки настила плюс толщина настила: h П = hбн + tн = 392 + 12 = 404 мм
Расход стали на настил и балки настила
m1 = r tн + mб/Lн = 7850 × 0,012+ 48,1/1,944 = 118,94 кг/м2.
2.1.2. Вариант 2. Балочная клетка усложненного типа
Расчет настила
Сбор нагрузки на 1 м2 настила
Таблица 2
| Наименование нагрузки | Нормативная нагрузка, кН/м2 | gf | Расчетная нагрузка, кН/м2 | |
| Временная нагрузка - Р | 1,2 | 14,4 | ||
| Собственный все настила gН = g´ tН = 77 × 0,006 | 0,462 | 1,05 | 0,485 | |
| Итого q = g +Р | qn = 12,462 | q = 14,885 |
Средний коэффициент 
Наибольший прогиб настила в зависимости от n0
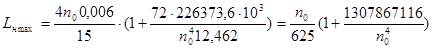
Принимаем пролет настила 0,875 м. Пролет укладывается по длине вспомогательной балки 8 раз. n0 = 120.
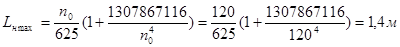
Проверка прогиба.
Балочный прогиб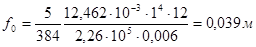 
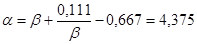
Прогиб настила: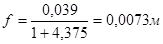 
- проверка проходит.
 |
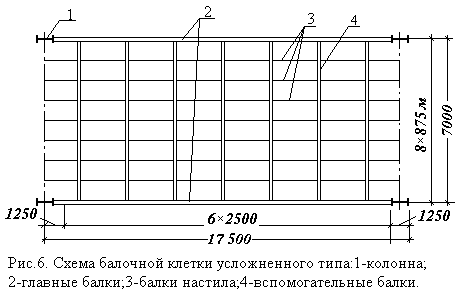Схема разбивки вспомогательной балки на панели 8 ´ 0,875 м.
Пролет балки настила принимаем 2,5 м.
Схема разбивки главной балки на панели 1,25 м + 6 ´ 2,5 м + 1,25 м (рис.6)
Проверка прогиба настила.
Балочный прогиб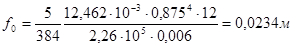 
Коэффициенты: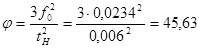 
,
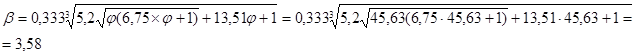
Прогиб настила: 
, 
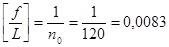- проверка жесткости настила удовлетворяется
Проверка прочности настила.
Изгибающий момент: 
Растягивающие усилия:
Момент сопротивления настила: 
Проверка нормальных напряжений
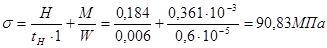
Rg gс = 1,1 × 230 = 253 МПа
s < gСRg - условие выполняется.
Расчет балки настила
Погонная нагрузка на балку настила:
а) нормативная от временной нагрузки, веса настила и балки настила:
qHб = qn LH + gHб = qn LH + 0,02 qn LH =12,462 × 0,875 + 0,02 × 12,462 × 0,875 = 11,12 кН/м
б) расчетная
qб = q LH + gHбgf = 14,885 × 0,875 + 1,05 × 0,218 = 13,25 кН/м
Изгибающий момент от расчетной нагрузки:
Требуемый момент сопротивления при с1 = 1,1 в первом приближении:
Требуемый по предельному прогибу момент инерции:
, где при 2,5 м n0 =142,5
По сортаменту подберем двутавр №10 ГОСТ 26020-83 (Jх=198 см4, Wх=39,7 см4, А=12 см2, mбн =9,5 кг/м, tw = 4,5 мм, t f =7,2 мм, h = 100 мм).
Уточним коэффициент с1=с по табл. 66 СНиП II-23-81*
Аw = tw (h- 2tf) = 4,5(100 - 2 × 7,2) = 385,2 мм2
Аf = (A - Aw) × 0,5 = (12,0 - 3,85) × 0,5 = 4,08 см2
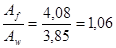Þ с = 1,07
Уточним нагрузку
а) нормативную qHб = qn LH + mбн g = 12,462 × 0,875 +9,5 × 10-3 × 9,81 = 11 кН/м
б) расчетную qб = q LH + mбн ggf = 14,885 × 0,875 + 0,093 × 1,05 = 13,12 кН/м
Максимальный изгибающий момент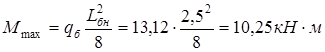 
Проверка нормальных напряжений
Rg gс = 1,1 × 230 = 253 МПа
s < gСRg - условие прочности выполняется с недонапряжением 3,7%.
Перерезывающая сила на опоре:
Qmax = qб L × 0,5= 13,12 ×2,5 × 0,5 = 16,4 кН
Проверка касательных напряжений.
RS gс = 0,58 × 1,1 × 230 = 146,7 МПа >42,58 МПа - проверка удовлетворяется
Проверка прогиба.
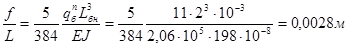
- условие выполняется.