Кафедра Педагогики и психологии дошкольного и начального образования
РЕФЕРАТ
по Методике преподавания математики в начальных классах
тема: «Уравнение»
Выполнено: студенткой 4 курса специальности «Преподавание в начальных классах» Пугиной Л.Е. Проверено: ст. пр. Болотова Т.В.
Алгебра - это особый раздел математики, зачатки которой родились еще в Вавилоне. Но название этой науке дал ученый Мухаммед бен Муса ал Хорезми из Ирана. Слово алгебра понималось, как «выполнение», «восстановление». Алгебра заменяет числовые знаения колличественных характеистик множеств или величин буквенной символикой. Способ решения задач при помощи составления уравнения называют алгебраическим.
Особое внимание в начальных классах уделяют решению уравнений, хотя решение уравнений является основным лишь в средней школе. В начальной школе осуществляется первичное ознакомление с уравнениями и способами их решения.
Ответ на вопрос, когда целесообразно знакомить детей с уравнением – в первом, во втором, третьем или четвертом классе, неоднозначен. Существуют две точки зрения на этот счет:
Одна точка зрения – познакомить с уравнениями как можно раньше и в процессе их решения осуществлять работу по усвоению детьми правил о взаимосвязи компонентов и результатов действий.
Другая точка зрения – приступать к решению уравнений после того, как учащиеся усвоят необходимую терминологию и те правила, которыми они будут пользоваться для решения уравнений.
В курсе математики начальных классов уравнение рассматривается как истинное равенство, содержащее неизвестное число.
Термин «решение» употребляется в двух смыслах: Он обозначает как число (корень), при подстановке которого уравнение обращается в верное равенство, так и сам процесс отыскания такого числа, то есть способ решения уравнения.
Методика обучения решению уравнений проходит в несколько этапов.
1. Подготовительный этап - начинается в первом классе. Учащиеся переходят к действиям над числами и выполняют задания, связанные с нахождением неизвестного числа в «окошке»,
например:
М1М ч.1 с.36
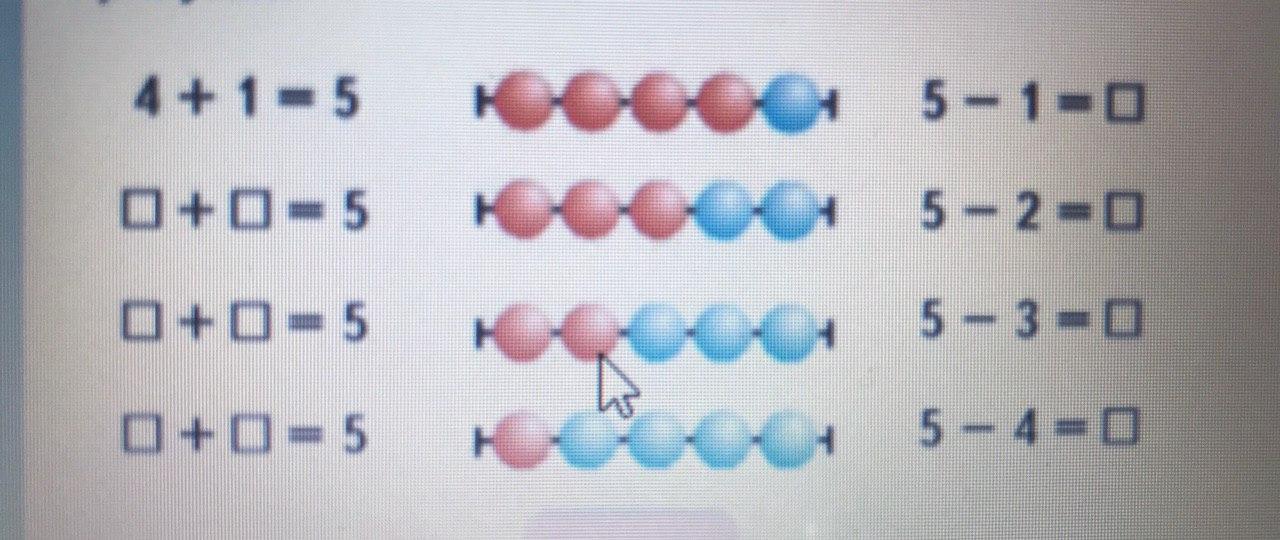
Дети находят число либо подбором, либо на основе знаний состава числа, либо на основе зависимости между компонентами и результатом действия.
На данном этапе учителю необходимо включать в устные упражнения следующие задания:
- Сколько надо вычесть из 5, чтобы получилось 4?
- Сколько надо вычесть из 4, чтобы получилось 3?
М1М ч.1 с.54

Подготовительную работу к решению уравнений мы можем наблюдать при выполнении действий с предметами.
М1М ч.1 с.45

Так же действия с окошечками используются и при решении задач.
М1М ч.1 с.67
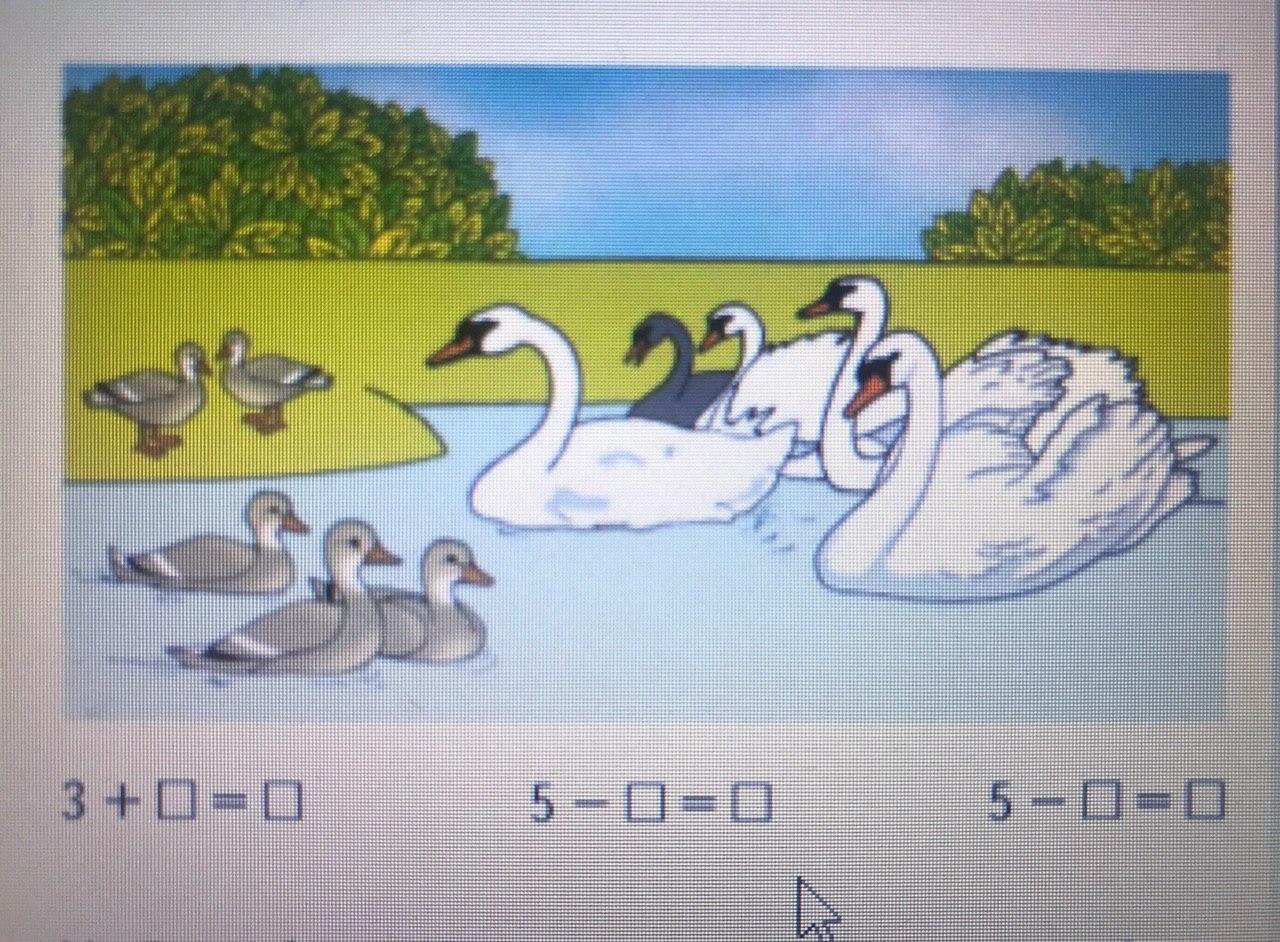
2. На втором этапе учащиеся знакомятся с понятиями «уравнение» и «корень уравнения». На протяжении нескольких уроков дети учатся решать уравнения с неизвестным слагаемым, уменьшаемым, вычитаемым. Названия компонентов арифметических действий были введены в речевую практику учащихся и использовались для чтения равенств и выражений.
По программе М.И. Моро тема «Уравнение» даетсяво втором классе, после того, как дети уже прошли тему: «Буквенные выражения, равенства и неравенства». М2М ч.1 с.76
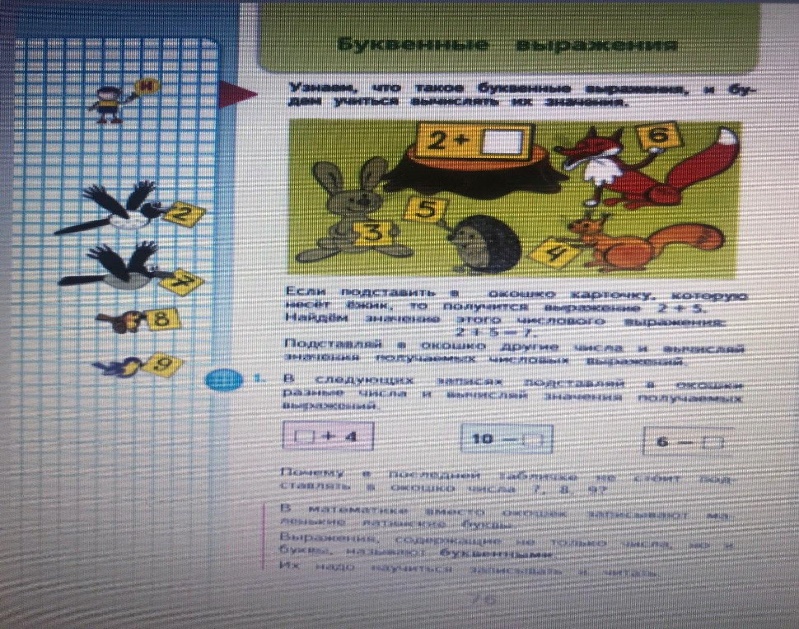
М2М ч.1 с.80

При введении используется такой прием.
Предлагаем карточку, на которой записано равенство с окошком.

… + 4=12
Дети подбирают число, которое нужно прибавить к 4, чтобы получить 12. Так как число мы меняли, то смысл окошка в данном случае в том, что это переменная величина.
Если мы используем другой способ и находим число, как неизвестное слагаемое по правилу, то в этом случае число в «окошке» – это неизвестная величина.
Поясняем, что вместо окошка для обозначения неизвестного числа используют латинские буквы. Получаем запись:
Х+4=12
Сообщаем:
Уравнение– это равенство, содержащее неизвестное число, которое надо найти. Решить уравнение – значит найти все такие значения х (если они есть), при которых, равенство будет верным.
То значение переменной, при котором уравнение обращается в истинное числовое равенство, называется корнем уравнения или решением уравнения.
Так же учащимся сообщается, как выполнить проверку при решении уравнения.
В начальных классах простейшие уравнения решают 1способом подбора и 2 на основе зависимости между компонентами и результатом действий.
В основе способа подбора лежит трактовка понятия «уравнения», как равенства, содержащего переменную. При одних значениях переменной уравнение может обращаться в истинное числовое равенство, при других – нет. То значение переменной, при которой уравнение обращается в истинное числовое равенство, называют корнем уравнения или решением уравнения.
Решение можно рассматривать в двух смыслах:
1) как корень уравнения;
2) как процесс решения.
При способе подбора решение уравнения записывают так:
Х+3=8 (подбор начинают с единицы)
1+3=4, 4<8
2+3=5, 5<8
3+3=6, 6<8
4+3=7, 7<8
5+3=8, 8=8
Х=5
Если рассматривать уравнение как истинное равенство, в котором есть неизвестное число, то в этом случае уравнение решают на основе зависимости между компонентами и результатом действий. Например:
Х +3=8 Х - это неизвестное слагаемое. Чтобы его найти…
Х=8 – 3
Х=5
5+3=8 Проверка: подставляем найденное значение вместо Х.
8=8
В последующих классах дети продолжают упражняться в решении уравнений:
М3М ч.1. с.7

М3М ч.1 с.8

В соответствии со стандартом по математике, в начальных классах изучают только простейшие уравнения в одно действие, но в некоторых программах и осложненные (в два и более действий).
Например, по программе И.Б. Истоминой в 4 классе М4И ч.2 с.86 изучают уравнения в два действия. Например:
(3+Х)•5=50 - неизвестен первый множитель (3+Х). Чтобы найти первый
множитель, надо произведение разделить на второй множитель.
3+Х=50:5
3+Х=10 - неизвестно второе слагаемое, значит надо из суммы вычесть
первое слагаемое.
Х=10-3
Х=7
__________
(3+7)•5=50
50=50
Главное объяснить учащимся, что в этом случае рассуждение надо начинать с последнего действия в левой части уравнения.
М4И ч.2 с.86.

3 этап. Решение задач алгебраическим способом, т.е. с помощью уравнения.
По некоторым программам (это превышает стандарт) показывают, как уравнение можно использовать при решении задач. Например, В М4И ч.2
предлагается задача: «В классе 25 учеников, из них 10 мальчиков, остальные девочки. Сколько девочек?» Строим схему.
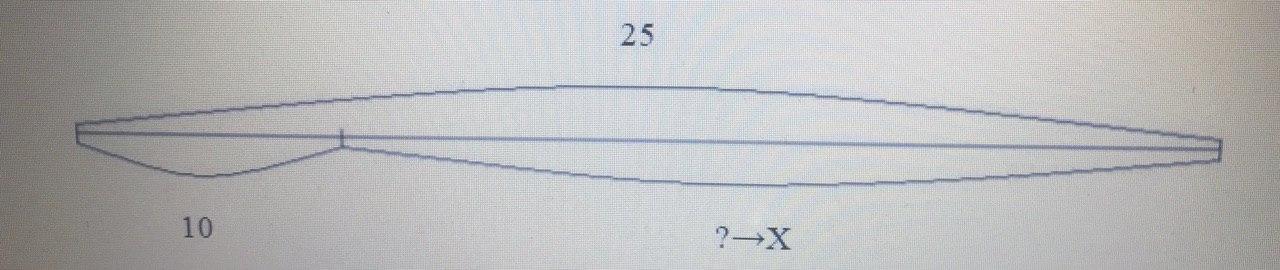
Затем учитель на схеме заменяет знак «?» буквой «Х» и по схеме составляют все возможные уравнения
10+Х=25 Х=25 – 10 25 – Х=10
Решая каждое из них, мы получаем одно и тоже значение (15). Следовательно, при решении задач с помощью уравнения достаточно составить одно уравнение и решить его. Т.к. это лишь подготовка к средней школе, то данное умение решать задачи с помощью уравнения полностью не отрабатывается.
Далее в М4И ч.2 идут более сложные задания. Например: М4И №502:
Масса трех одинаковых баранов 180 кг. Свинья тяжелее барана на 40 кг. Какова масса свиньи? Решим задачу с помощью уравнения.
Даны рассуждения Маши и Миши.

При решении задач с помощью уравнений у детей часто возникают сложности. Можно использовать следующие методические приемы, помогающие в их решении:
1) дать готовый образец уравнения и попросить прокомментировать (Как сделано в №502)
2) дополни начатое уравнение;
3) исправь ошибки в рассуждении при составлении уравнения (М4И, с.154)
4) выбери правильное уравнение из нескольких предложенных.

По программе И.И. Аргинской тему «Уравнения» начинают изучать во втором классе, предварительно изучив латинские буквы
М1А ч.1 с.52

М2А ч.1 с.30

Вводится определение:

Даются задания для закрепления:
М2А ч.1 с.32-33

После дети изучают ряд правил:
М2А ч.1 с.36

М2А ч.1 с.40

М2А ч.1 с.44

М2А ч.1 с.46

Вначале дают простые уравнения, в 3 классе уже вводят более сложные
М3А ч.1 с.63

При решении уравнений используют следующие методические приемы, помогающие в их решении:
1) Сравни уравнения
(у + 279) + 384 = 819 (у + 279) + 320 = 755
(у +279) + 352 + 787 (у + 279) + 288 = 723
У них будут разные корни? Объясни свой ответ.
2) Предложи способ решения уравнений и реши их. При затруднении подумай, не помогут ли тебе свойства сложения.
3) Сравни найденные корни. Твое мнение оказалось верным?
М3А ч.2 с.7

М3А ч.2 с.29

М3А ч.2 с.107


В 4 классе на протяжении всего года, детям даются практические задания, связанные с уравнениями:
М4А ч.1 с.11

М4А ч.1 с.21

М4А ч.1 с.50

М4А ч.1 с.55

Детям предлагают практические задания на решение уравнений разными способами:
М4А ч.1 с.80

По программе И.И. Аргинской учащихся знакомят и с третьим способом решения уравнении, на основе свойств равенств, сначала изучают эти свойства: «Если к обеим частям верного равенства прибавить (вычесть, умножить, разделить) одно и тоже число, то равенство останется верным».
М4А ч.1 с.92

М4А ч.1 с.93

Таким образом, на основе этих правил можно решить уравнения. Например,
Х+4=9
Х+4-4=9-4 - вычтем из обеих частей равенства число 4, получим
Х=5 верное равенство
5+4=9
9=9
Этим способом по программе И.И. Аргинской решают не только простейшие, но и осложненные уравнения.
М4А ч.1 с.98

М4А ч.1 с.110

Учащимся предлагают практические задания на закрепление данного способа решения уравнений:
М4А ч.1 с.111

Во втором полугодии 4 класса, дети продолжают решать уравнения и задачи с помощью уравнений: М4А ч.2 с.23


Решение задач с помощью усложненных уравнений:

Рассматривая программу А.Л. Чекина, мы наблюдаем, что тема «Уравнение» вводится во втором полугодии 2 класса
М2Ч ч.2 с.84-85

Вначале решают простые уравнения, но вскоре вводится решение задач с помощью уравнений
М2Ч ч.2 с.148
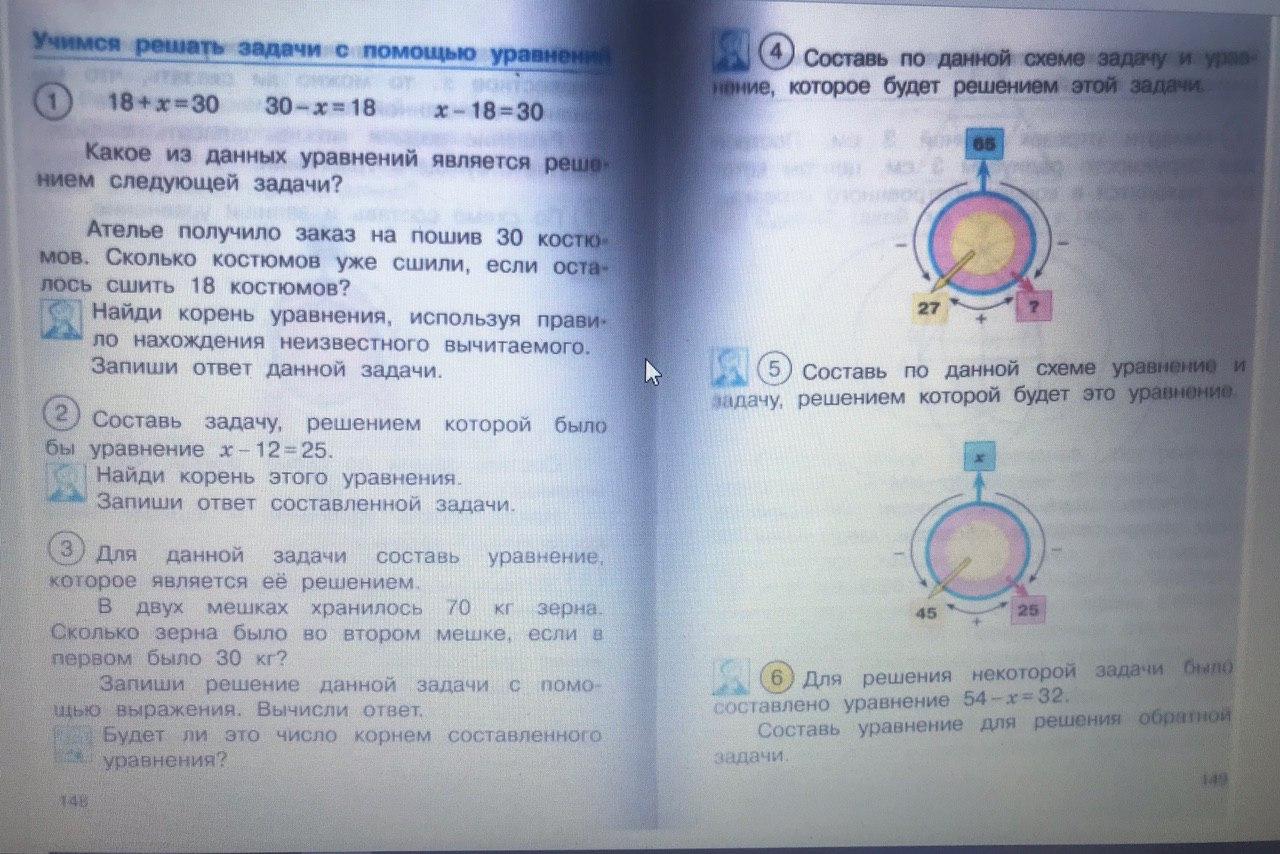
В каждом последующем классе, темы «Уравнение» касаются во втором полугодии и уделяют на мой взгляд не очень много времени, но тем не менее предлагая учащимся к концу 4 класса задачи с усложненными уравнениями
М3Ч ч.2 с.32-34

М4Ч ч.2 с.92-95


Делая вывод, можно сказать, что все программы составлены так, чтобы дети к концу начальной школы получили уровень знаний, предусмотренный ФГОС, то есть обязательный минимум. Задания повышенной сложности, которые ассоциируются только с развивающими системами, есть во всех комплексах, но не являются обязательными для усвоения. Каждая система рассчитана на определенный склад ума, или, иначе говоря на разные способы восприятия и обработки информации. Авторство же проявляется в способах подачи материала. Практически у всех авторских обучающих программ есть как достоинства, так и недостатки.