МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ЭКОНОМИКИ, СТАТИСТИКИ И ИНФОРМАТИКИ
Семестровая работа по курсу
«Диагностика кризисного состояния предприятия»
Выполнила:
Шкляева Виктория Викторовна
Группа: ДЭС-401
Проверил:
д.т.н., профессор
Фомин Ярослав Алексеевич
Москва, 2011
Введение.
В данной работе будет производиться анализ Австралии, а также стран Восточной и Западной Европы, которые предварительно разделены на 2 группы: передовые страны и отстающие. За основу дискриминации взяты несколько основных показателей социально-экономического развития страны. Для первоначального разбиения использовался показатель «Ожидаемая продолжительность жизни»
Кроме того, проводится сравнение уровня развития России и других стран в динамике за 2007-2010 годы.
Исходные данные.
| Признак | ||||
| Передовые страны S1 | ||||
| X1(1) | X2(1) | X3(1) | X4(1) | |
| Ожидаемая продолжительность жизни | 76,9 | 78,1 | 76,8 | 75,8 |
| ВВП на душу населения | 29,53 | 37,3 | 29,29 | 33,74 |
| Занятость, млн | 19,39 | 10,76 | 23,00 | 25,38 |
X1(1) – Испания
X2(1) – Австралия
X3(1) – Италия
X4(1) – Франция
| Признак | Отстающие страны S2 | |||
| X1(1) | X2(1) | X3(1) | X4(1) | |
| Ожидаемая продолжительность жизни | 62,71 | 62,6 | 58,8 | 64,5 |
| ВВП на душу населения | 12,48 | 64,6 | 15,04 | 27,66 |
| Занятость, млн | 9,356 | 7,567 | 16,346 | 5,164 |
X1(1) – Беларусь
X2(1) – Украина
X3(1) – Россия
X4(1) – Молдавия
Обучение с тремя показателями.
1. Для групп стран S1 и S2 составим векторы средних (соответственно а1 и а2), а также их разность.
| 76,90 | 62,15 | 14,75 | 139,05 | ||||
| а1= | 32,47 | а2= | 29,95 | а1+а2= | 2,52 | а1-а2= | 62,41 |
| 19,63 | 9,61 | 10,02 | 29,24 |
2. Вычислим ковариационные матрицы М1 и М2, где m1 и m2 количество передовых и отсталых стран
2.1. Ковариационная матрица М1

| 0,00 | ||||||
| (X1(1)-a1)= | -2,94 | (X1(1)-a1)T= | 0,00 | -2,94 | -0,24 | |
| -0,24 | ||||||
| 1,20 | ||||||
| (X2(1)-a1)= | 4,83 | (X2(1)-a1)T= | 1,2 | 4,835 | -8,873 | |
| -8,87 | ||||||
| -0,10 | ||||||
| (X3(1)-a1)= | -3,18 | (X3(1)-a1)T= | -0,1 | -3,175 | 3,363 | |
| 3,36 | ||||||
| -1,10 | ||||||
| (X4(1)-a1)= | 1,28 | (X4(1)-a1)T= | -1,1 | 1,275 | 5,752 | |
| 5,75 |
| (X1(1)-a1)(X1(1)-a1)T = | 8,614225 | 0,71027 | |||
| 0,71027 | 0,058564 | ||||
| 1,44 | 5,802 | -10,6476 | |||
| (X2(1)-a1)(X2(1)-a1)T = | 5,802 | 23,377225 | -42,900955 | ||
| -10,6476 | -42,900955 | 78,730129 | |||
| 0,01 | 0,3175 | -0,3363 | |||
| (X3(1)-a1)(X3(1)-a1)T = | 0,3175 | 10,080625 | -10,677525 | ||
| -0,3363 | -10,677525 | 11,309769 | |||
| 1,21 | -1,4025 | -6,3272 | |||
| (X4(1)-a1)(X4(1)-a1)T = | -1,4025 | 1,625625 | 7,3338 | ||
| -6,3272 | 7,3338 | 33,085504 | |||
| 2,66 | 4,717 | -17,3111 | |||
| Сумма = | 4,717 | 43,6977 | -45,53441 | ||
| -17,3111 | -45,53441 | 123,183966 | |||
| 0,886666667 | 1,572333333 | -5,770366667 | |||
| М1 = | 1,572333333 | 14,5659 | -15,17813667 | ||
| -5,770366667 | -15,17813667 | 41,061322 | |||
2.2. Ковариационная матрица М2

| 0,56 | ||||||
| (X1(2)-a2)= | -17,47 | (X1(2)-a2)T= | 0,56 | -17,47 | -0,25 | |
| -0,25 | ||||||
| 0,45 | ||||||
| (X2(2)-a2)= | 34,66 | (X2(2)-a2)T= | 0,45 | 34,66 | -2,04 | |
| -2,04 | ||||||
| -3,35 | ||||||
| (X3(2)-a2)= | -14,91 | (X3(2)-a2)T= | -3,35 | -14,91 | 6,74 | |
| 6,74 | ||||||
| 2,35 | ||||||
| (X4(2)-a2)= | -2,29 | (X4(2)-a2)T= | 2,35 | -2,29 | -4,44 | |
| -4,44 |
| 0,31 | -9,74 | -0,14 | |
| (X1(2)-a2)(X1(2)-a2)T = | -9,74 | 305,03 | 4,41 |
| -0,14 | 4,41 | 0,06 | |
| 0,20 | 15,51 | -0,91 | |
| (X2(2)-a2)(X2(2)-a2)T = | 15,51 | 1200,97 | -70,74 |
| -0,91 | -70,74 | 4,17 | |
| 11,24 | 49,97 | -22,59 | |
| (X3(2)-a2)(X3(1)-a2)T = | 49,97 | 222,16 | -100,43 |
| -22,59 | -100,43 | 45,40 | |
| 5,51 | -5,36 | -10,43 | |
| (X4(2)-a2)(X4(2)-a2)T = | -5,3640375 | 5,221225 | 10,15511 |
| -10,432877 | 10,15511 | 19,75136 | |
| 17,26 | 50,38 | -34,08 | |
| Сумма = | 50,38 | 1733,38 | -156,61 |
| -34,08 | -156,61 | 69,38 | |
| 5,75369167 | 16,79212 | -11,35842 | |
| М2 = | 16,7921167 | 577,7918 | -52,20168 |
| -11,358424 | -52,20168 | 23,12632 |
3. Найдём общую ковариационную матрицу М

| 4,426905556 | 12,24296667 | -11,41919389 | |
| М = | 12,24296667 | 394,9051556 | -44,91987444 |
| -11,41919389 | -44,91987444 | 42,79176239 |
4. Найдём обратную матрицу М-1
| 0,7249272348 | -0,0005334017 | 0,1928904970 | |
| M-1 = | -0,0005334017 | 0,0028760105 | 0,0028766988 |
| 0,1928904970 | 0,0028766988 | 0,0778625312 |
5. Найдём произведение транспонированной разности векторов средних групп стран (а1-а2)Т и обратной общей ковариационной матрицы M-1
| (а1-а2)T = | 14,7475 | 2,52 | 10,02375 |
| 1/2*(а1-а2)T = | 7,37375 | 1,26 | 5,011875 |
| (а1-а2)T M-1 = | 12,62300634 | 0,028216515 | 3,632376433 |
| 1/2 (а1-а2)T M-1 = | 6,311503171 | 0,014108258 | 1,816188216 |
Для определения достоверности:
- Вычислим расстояние Махаланобиса:

 =222,638
=222,638
 =14,92
=14,92
- Найдем
 и
и 

 0,707
0,707

 2,121
2,121
- Найдем

p=3
 =0,00441
=0,00441
 = 0,0567
= 0,0567
 = 0,00
= 0,00
 = 1,125
= 1,125
 =0,0132
=0,0132
Достоверность прогноза равна  = 0,9868
= 0,9868
Обучение с четырьмя показателями.
Добавим ещё один показатель – внешний государственный долг.
| Признак | Передовые страны S1 | |||
| X1(1) | X2(1) | X3(1) | X4(1) | |
| Ожидаемая продолжительность жизни | 76,9 | 78,1 | 76,8 | 75,8 |
| ВВП на душу населения | 29,53 | 37,3 | 29,29 | 33,74 |
| Занятость, млн | 19,39 | 10,76 | 23,00 | 25,38 |
| внешний долг | 1,084 | 0,826 | 0,9996 | 4,396 |
X1(1) – Испания
X2(1) – Австралия
X3(1) – Италия
X4(1) – Франция
| Признак | Отстающие страны S2 | |||
| X1(1) | X2(1) | X3(1) | X4(1) | |
| Ожидаемая продолжительность жизни | 62,71 | 62,6 | 58,8 | 64,5 |
| ВВП на душу населения | 12,48 | 64,6 | 15,04 | 27,66 |
| Занятость, млн | 9,356 | 7,567 | 16,346 | 5,164 |
| внешний долг | 0,0734 | 0,06904 | 0,356 | 0,033 |
X1(1) – Беларусь
X2(1) – Украина
X3(1) – Россия
X4(1) – Молдавия
1. Для групп стран S1 и S2 составим векторы средних (соответственно а1 и а2), а также их разность.
| 76,9 | 62,1525 | 14,7475 | |||
| а1= | 32,465 | а2= | 29,945 | а1-а2= | 2,52 |
| 19,632 | 9,60825 | 10,02375 | |||
| 1,8264 | 0,13286 | 1,69354 |
2. Вычислим ковариационные матрицы М1 и М2, где m1 и m2 количество преуспевающих и кризисных предприятий соответственно
2.1. Ковариационная матрица М1

| (X1(1)-a1)= | -2,935 | (X1(1)-a1)T= | -2,935 | -0,242 | -0,7424 | ||
| -0,242 | |||||||
| -0,7424 | |||||||
| 1,2 | |||||||
| (X2(1)-a1)= | 4,835 | (X2(1)-a1)T= | 1,2 | 4,835 | -8,873 | -1,0004 | |
| -8,873 | |||||||
| -1,0004 | |||||||
| -0,1 | |||||||
| (X3(1)-a1)= | -3,175 | (X3(1)-a1)T= | -0,1 | -3,175 | 3,363 | -0,8268 | |
| 3,363 | |||||||
| -0,8268 | |||||||
| -1,1 | |||||||
| (X4(1)-a1)= | 1,275 | (X4(1)-a1)T= | -1,1 | 1,275 | 5,752 | 2,5696 | |
| 5,752 | |||||||
| 2,5696 |
| (X1(1)-a1)(X1(1)-a1)T = | 8,614225 | 0,71027 | 2,178944 | |
| 0,71027 | 0,058564 | 0,1796608 | ||
| 2,178944 | 0,1796608 | 0,55115776 | ||
| 1,44 | 5,802 | -10,6476 | -1,20048 | |
| (X2(1)-a1)(X2(1)-a1)T = | 5,802 | 23,377225 | -42,900955 | -4,836934 |
| -10,6476 | -42,900955 | 78,730129 | 8,8765492 | |
| -1,20048 | -4,836934 | 8,8765492 | 1,00080016 | |
| 0,01 | 0,3175 | -0,3363 | 0,08268 | |
| (X3(1)-a1)(X3(1)-a1)T = | 0,3175 | 10,080625 | -10,677525 | 2,62509 |
| -0,3363 | -10,677525 | 11,309769 | -2,7805284 | |
| 0,08268 | 2,62509 | -2,7805284 | 0,68359824 | |
| 1,21 | -1,4025 | -6,3272 | -2,82656 | |
| (X4(1)-a1)(X4(1)-a1)T = | -1,4025 | 1,625625 | 7,3338 | 3,27624 |
| -6,3272 | 7,3338 | 33,085504 | 14,7803392 | |
| -2,82656 | 3,27624 | 14,7803392 | 6,60284416 | |
| 2,66 | 4,717 | -17,3111 | -3,94436 | |
| Сумма = | 4,717 | 43,6977 | -45,53441 | 3,24334 |
| -17,3111 | -45,53441 | 123,183966 | 21,0560208 | |
| -3,94436 | 3,24334 | 21,0560208 | 8,83840032 | |
| 0,886666667 | 1,572333333 | -5,770366667 | -1,314786667 | |
| М1 = | 1,572333333 | 14,5659 | -15,17813667 | 1,081113333 |
| -5,770366667 | -15,17813667 | 41,061322 | 7,0186736 | |
| -1,314786667 | 1,081113333 | 7,0186736 | 2,94613344 |
2.2. Ковариационная матрица М2

| 0,5575 | |||||||||
| (X1(2)-a2)= | -17,465 | (X1(2)-a2)T= | 0,5575 | -17,465 | -0,25225 | -0,05946 | |||
| -0,25225 | |||||||||
| -0,05946 | |||||||||
| 0,4475 | |||||||||
| (X2(2)-a2)= | 34,655 | (X2(2)-a2)T= | 0,4475 | 34,655 | -2,04125 | -0,06382 | |||
| -2,04125 | |||||||||
| -0,06382 | |||||||||
| -3,3525 | |||||||||
| (X3(2)-a2)= | -14,905 | (X3(2)-a2)T= | -3,3525 | -14,905 | 6,73775 | 0,22314 | |||
| 6,73775 | |||||||||
| 0,22314 | |||||||||
| 2,3475 | |||||||||
| (X4(2)-a2)= | -2,285 | (X4(2)-a2)T= | 2,3475 | -2,285 | -4,44425 | -0,09986 | |||
| -4,44425 | |||||||||
| -0,09986 | |||||||||
| 0,310806 | -9,736737 | -0,14063 | -0,03315 | |
| (X1(2)-a2)(X1(2)-a2)T = | -9,73674 | 305,02623 | 4,405546 | 1,038469 |
| -0,14063 | 4,4055463 | 0,06363 | 0,014999 | |
| -0,03315 | 1,0384689 | 0,014999 | 0,003535 | |
| (X2(2)-a2)(X2(2)-a2)T = | 0,200256 | 15,508112 | -0,91346 | -0,02856 |
| 15,50811 | 1200,969 | -70,7395 | -2,21168 | |
| -0,91346 | -70,73952 | 4,166702 | 0,130273 | |
| -0,02856 | -2,211682 | 0,130273 | 0,004073 | |
| (X3(2)-a2)(X3(2)-a2)T = | 11,23926 | 49,969013 | -22,5883 | -0,74808 |
| 49,96901 | 222,15903 | -100,426 | -3,3259 | |
| -22,5883 | -100,4262 | 45,39728 | 1,503462 | |
| -0,74808 | -3,325902 | 1,503462 | 0,049791 | |
| (X4(2)-a2)(X4(2)-a2)T = | 5,510756 | -5,364037 | -10,4329 | -0,23442 |
| -5,36404 | 5,221225 | 10,15511 | 0,22818 | |
| -10,4329 | 10,155111 | 19,75136 | 0,443803 | |
| -0,23442 | 0,2281801 | 0,443803 | 0,009972 | |
| Сумма = | 17,26108 | 50,37635 | -34,0753 | -1,04421 |
| 50,37635 | 1733,3755 | -156,605 | -4,27093 | |
| -34,0753 | -156,605 | 69,37896 | 2,092536 | |
| -1,04421 | -4,270935 | 2,092536 | 0,067372 | |
| М2 = | 5,753692 | 16,792117 | -11,3584 | -0,34807 |
| 16,79212 | 577,79183 | -52,2017 | -1,42364 | |
| -11,3584 | -52,20168 | 23,12632 | 0,697512 |
Найдём общую ковариационную матрицу М

| 4,426905556 | 12,24296667 | -11,41919389 | -1,108570356 | |
| 12,24296667 | 394,9051556 | -44,91987444 | -0,2283544 | |
| М = | -11,41919389 | -44,91987444 | 42,79176239 | 5,144123667 |
| -1,108570356 | -0,2283544 | 5,144123667 | 1,979060507 |
Найдём обратную матрицу М-1
| 0,753781 | 0,001719 | 0,221332 | -0,152874 | |
| 0,001719 | 0,003052 | 0,005097 | -0,011933 | |
| M-1 = | 0,221332 | 0,005097 | 0,105898 | -0,150690 |
| -0,152874 | -0,011933 | -0,150690 | 0,809966 |
Найдём произведение транспонированной разности векторов средних групп стран (а1-а2)Т и обратной общей ковариационной матрицы M-1
| (а1-а2)T = | 14,7475 | 2,52 | 10,02375 | 1,69354 | ||
| 1/2*(а1-а2)T = | 7,37375 | 1,26 | 5,011875 | 0,84677 | ||
| (а1-а2)T M-1 = | 13,08039359 | 0,063918938 | 4,083228781 | -2,423352416 | ||
| 1/2 (а1-а2)T M-1 = | 6,540196796 | 0,031959469 | 2,04161439 | -1,211676208 | ||
Для определения достоверности:
- Вычислим расстояние Махаланобиса:

 =15,162
=15,162
- Найдем
 и
и 

 0,707
0,707

 2,121
2,121
- Найдем

p=4
 =7,147
=7,147
 = 0,00558
= 0,00558
 = 0,008066
= 0,008066
 = 1,19324
= 1,19324
 =0,05288
=0,05288
Достоверность прогноза равна  = 0,94712
= 0,94712
Итак,  = 1,016 <
= 1,016 <  =2.
=2.
Оптимальная размерность признакового пространства р=4.
Сравнение
Для определения положения России среди развитых и отстающих стран построим график, учитывая положение других государств.
1. Испания.
| Признак | ||||
| Ожидаемая продолжительность жизни | 76,9 | 76,8 | 77,2 | 77,2 |
| ВВП на душу населения | 29,53 | 30,23 | 31,19 | 32,3 |
| Занятость, млн | 19,39 | 18,61 | 19,94 | 20,08 |
| внешний долг | 1,084 | 1,56 | 1,94 | 2,03 |
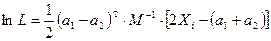
| Xi | X1 | X2 | X3 | X4 | |
| 2 Xi –(a1+a2) | 14,7 | 14,5 | 15,3 | 15,3 | |
| -3,3 | -2,0 | 0,0 | 2,2 | ||
| 9,5 | 8,0 | 10,6 | 10,9 | ||
| 0,2 | 1,2 | 1,9 | 2,1 | ||
| ln L | 115,568 | 109,966 | 119,770 | 120,194 |
2. Австралия
| Признак | ||||
| Ожидаемая продолжительность жизни | 78,1 | 78,1 | 78,4 | 78,5 |
| ВВП на душу населения | 37,3 | 37,9 | 38,2 | 38,7 |
| Занятость, млн | 10,756 | 10,986 | 11,345 | 12,627 |
| внешний долг | 0,826 | 0,758 | 0,923 | 0,876 |
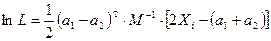
| Xi | X1 | X2 | X3 | X4 | |
| 2 Xi –(a1+a2) | 17,1 | 17,1 | 17,7 | 17,9 | |
| 12,2 | 13,4 | 14,0 | 15,0 | ||
| -7,7 | -7,3 | -6,6 | -4,0 | ||
| -0,3 | -0,4 | -0,1 | -0,2 | ||
| ln L | 97,132 | 98,274 | 103,283 | 109,972 |
3. Италия
| Признак | ||||
| Ожидаемая продолжительность жизни | 76,8 | 76,8 | 76,9 | 76,9 |
| ВВП на душу населения | 29,29 | 30,08 | 30,69 | 31,87 |
| Занятость, млн | 22,995 | 22,43 | 21,368 | 22,642 |
| внешний долг | 0,9996 | 1,064 | 1,361 | 0,899 |
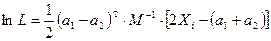
| Xi | X1 | X2 | X3 | X4 | |
| 2 Xi –(a1+a2) | 14,5 | 14,5 | 14,7 | 14,7 | |
| -3,8 | -2,3 | -1,0 | 1,3 | ||
| 16,7 | 15,6 | 13,5 | 16,0 | ||
| 0,0 | 0,2 | 0,8 | -0,2 | ||
| ln L | 129,169 | 126,757 | 123,048 | 129,445 |
4. Беларусь
| Признак | ||||
| Ожидаемая продолжительность жизни | 62,7 | 63,6 | 64,2 | 64,6 |
| ВВП на душу населения | 12,48 | 12,97 | 13,61 | 13,27 |
| Занятость, млн | 9,356 | 8,521 | 7,358 | 7,842 |
| внешний долг | 0,0734 | 0,0726 | 0,733 | 0,0715 |
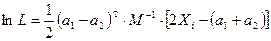
| Xi | X1 | X2 | X3 | X4 | |
| 2 Xi –(a1+a2) | -13,7 | -11,9 | -10,7 | -9,9 | |
| -37,5 | -36,5 | -35,2 | -35,9 | ||
| -10,5 | -12,2 | -14,5 | -13,6 | ||
| -1,8 | -1,8 | -0,5 | -1,8 | ||
| ln L | -109,785 | -101,389 | -99,849 | -91,060 |
5. Россия
| Признак | ||||
| Ожидаемая продолжительность жизни | 58,8 | 60,4 | 61,4 | 60,3 |
| ВВП на душу населения | 15,04 | 16,31 | 16,85 | 17,48 |
| Занятость, млн | 16,346 | 17,658 | 18,024 | 18,954 |
| внешний долг | 0,356 | 0,457 | 0,568 | 0,542 |
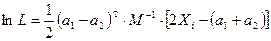
| Xi | X1 | X2 | X3 | X4 | |
| 2 Xi –(a1+a2) | -21,5 | -18,3 | -16,3 | -18,5 | |
| -32,3 | -29,8 | -28,7 | -27,5 | ||
| 3,5 | 6,1 | 6,8 | 8,7 | ||
| -1,2 | -1,0 | -0,8 | -0,9 | ||
| ln L | -132,778 | -106,656 | -92,316 | -102,804 |
Динамика развития стран

Вывод.
Анализируя график, можно сказать, что наиболее развитыми являются страны Западной Европы и Австралия. При этом, положение Италии несколько лучше, чем Испании и Австралии.
К отсталым относится Россия и Беларусь, но стоит отметить, что развитие РФ идет резче. Заметно, что до 2009 шел значительный подъем, но уже в 2010 году наблюдается небольшой спад. В целом, можно говорить о положительной динамике развития.