Министерство образования и науки Российской Федерации
Федеральное государственное бюджетное образовательное учреждение
высшего профессионального образования
«НАЦИОНАЛЬНЫЙ ИССЛЕДОВАТЕЛЬСКИЙ
ТОМСКИЙ ПОЛИТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ»
Институт ИНК
Направление подготовки Приборостроение
Кафедра ИИТ
ОТЧЕТ
По лабораторной работе
Динамические звенья II порядка
Основы Автоматического Управления
Выполнил студент гр. 1Б3Б Машанов А.П.
Отчет принял преподаватель Казьмин В.П.
Томск 2015 г.
Цель работы: исследование переходных процессов, вызванных ступенчатым воздействием в динамических звеньях второго порядка, определение характера переходных процессов, типа корней характеристического уравнения и устойчивости звеньев.
Ведение
К динамическим звеньям второго порядка относятся следующие типы звеньев: апериодическое второго порядка, колебательное (периодическое) и консервативное [3]. Дифференциальное уравнение в общем виде, передаточная функция 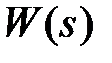 и характеристическое уравнение, соответственно имеют вид:
и характеристическое уравнение, соответственно имеют вид:
 , (4.2.1)
, (4.2.1)
 , (4.2.2)
, (4.2.2)
 . (4.2.3)
. (4.2.3)
Вид графиков (сходящийся либо расходящийся, либо колебательный с постоянной амплитудой и частотой); характер переходного процесса (периодический либо апериодический); тип звена (апериодическое второго порядка, колебательное либо консервативное); устойчивость звена (устойчивое, неустойчивое, нейтральное) определяется корнями характеристического уравнения (4.2.3) (левые, правые, нулевые, вещественные, комплексные, мнимые) [3].
Если корни уравнения (4.2.3) вещественные,  ;
; 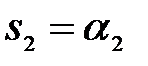 , то согласно формуле (4.1.8) решение дифференциального уравнения (4.2.1) можно представить как сумму экспонент:
, то согласно формуле (4.1.8) решение дифференциального уравнения (4.2.1) можно представить как сумму экспонент:
 , (4.2.4)
, (4.2.4)
где: 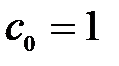 ,
,  ,
,  ,
,
и звено в данном случае является апериодическим второго порядка.
Если корни уравнения (4.2.3) являются комплексно-сопряженными 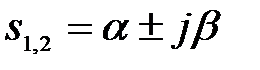 , то звено является периодическим (колебательным), а решение уравнения (4.2.1) можно записать
, то звено является периодическим (колебательным), а решение уравнения (4.2.1) можно записать
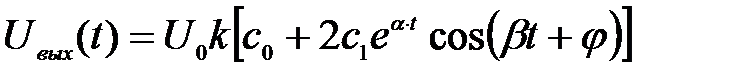 . (4.2.5)
. (4.2.5)
Пояснение:
Для определения 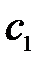 и
и 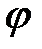 воспользуемся суммой формулы (4.1.8)
воспользуемся суммой формулы (4.1.8)

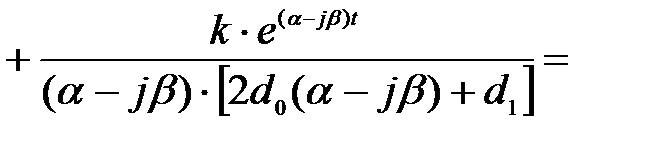
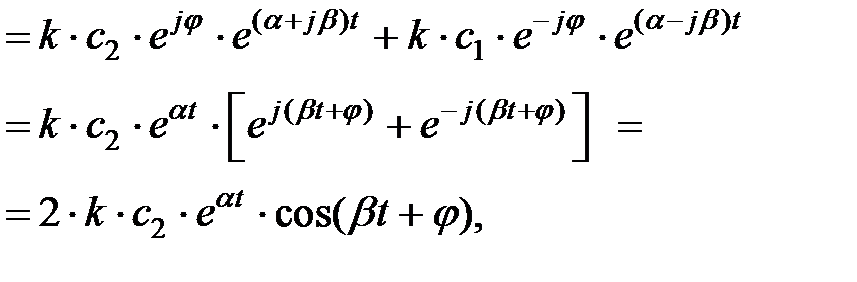
где
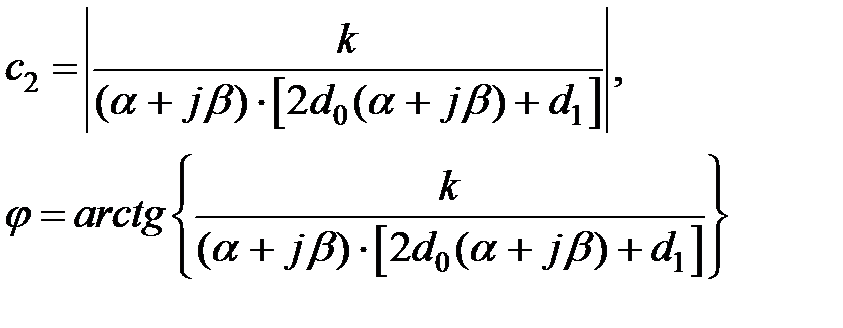
Если в уравнении (4.2.3)  , то звено является консервативным, при этом корни мнимые
, то звено является консервативным, при этом корни мнимые  , и уравнение (4.2.5) запишется:
, и уравнение (4.2.5) запишется:
 . (4.2.6)
. (4.2.6)
В уравнения (4.2.3-4.2.6) входит экспонента  , следовательно, переходный процесс в звене сходится к установившемуся значению
, следовательно, переходный процесс в звене сходится к установившемуся значению 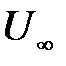 , расходится от него, либо колеблется с постоянной амплитудой и устойчивость, неустойчивость или нейтральность звена зависит от
, расходится от него, либо колеблется с постоянной амплитудой и устойчивость, неустойчивость или нейтральность звена зависит от 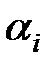 , то есть от корней
, то есть от корней 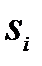 [3].
[3].
Динамическое звено II порядка

Докажем, что данная схема действительно является моделью динамического звена второго порядка. Для этого найдем эквивалентную передаточную функцию:
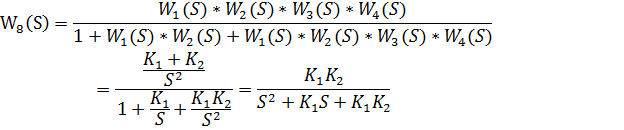
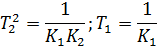
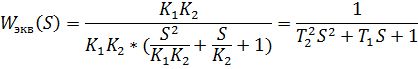
Для того, чтобы процесс был устойчивым, 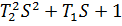 должно быть <0.
должно быть <0.
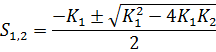
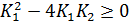 – условие для вещественных отрицательных корней
– условие для вещественных отрицательных корней
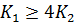
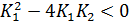 – условие для комплексных корней
– условие для комплексных корней

Графики переходного процесса при отрицательных вещественных корнях характеристического уравнения (Апериодический процесс). 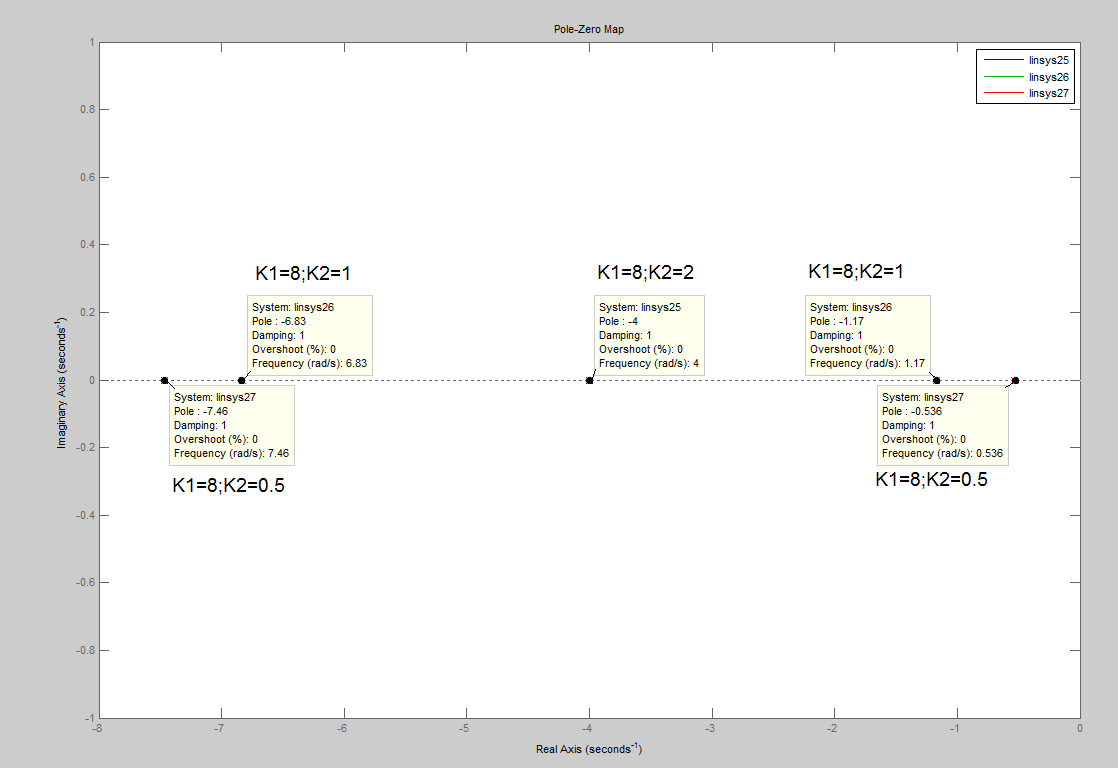
Отрицательные вещественные корни характеристического уравнения.

Графики переходного процесса при комплексных корнях характеристического уравнения (Колебательный процесс).
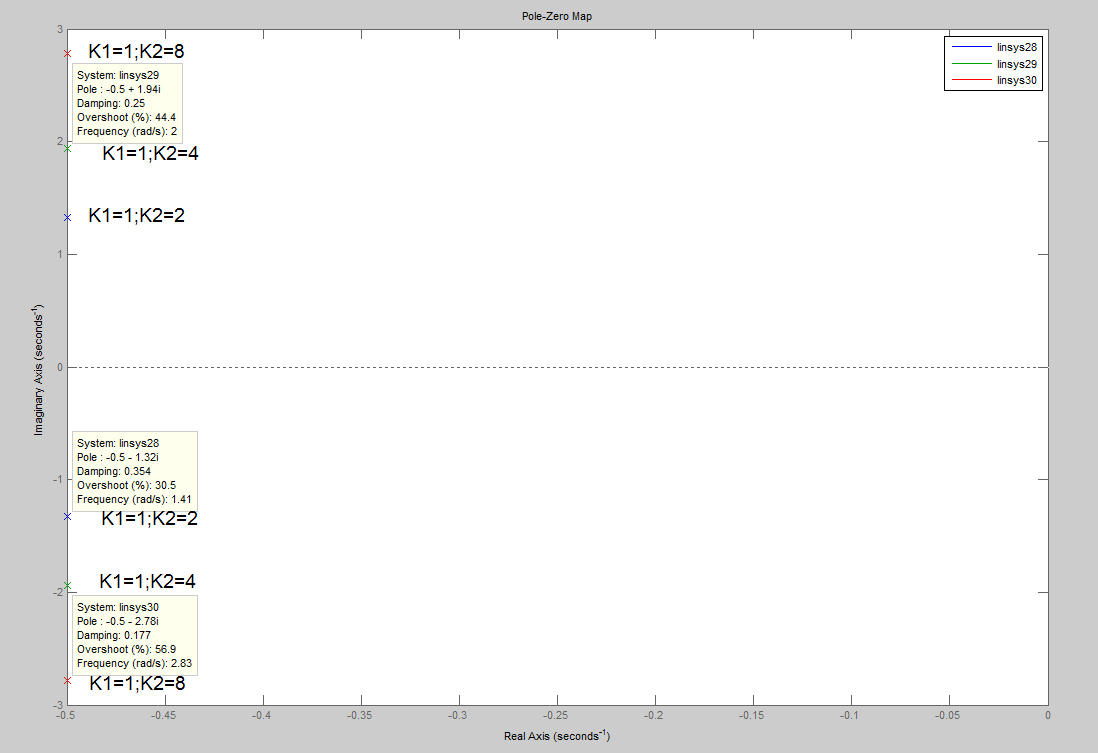
Комплексные корни характеристического уравнения.
Вывод: при выполнении условия 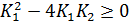 чем больше разница между коэффициентами
чем больше разница между коэффициентами 
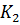 , тем больше разница между вещественными отрицательными корнями, и тем больше время переходного процесса, наименьшее время переходного процесса достигается при равенстве корней характеристического уравнения (
, тем больше разница между вещественными отрицательными корнями, и тем больше время переходного процесса, наименьшее время переходного процесса достигается при равенстве корней характеристического уравнения (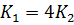 ). При
). При 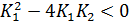 , при увеличении разницы между коэффициентами
, при увеличении разницы между коэффициентами 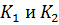 увеличивается мнимая часть корней, вещественная остается одинаковой, амплитуда колебаний в переходном процессе увеличивается.
увеличивается мнимая часть корней, вещественная остается одинаковой, амплитуда колебаний в переходном процессе увеличивается.
Динамическое звено II порядка с коэффициентами обратной связи 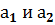

Докажем, что данная схема действительно является моделью динамического звена второго порядка с коэффициентами обратной связи 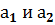 . Для этого найдем эквивалентную передаточную функцию:
. Для этого найдем эквивалентную передаточную функцию:

Для того, чтобы процесс был устойчивым, 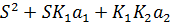 должно быть <0.
должно быть <0.
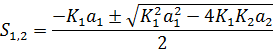
Для того чтобы процесс имел незатухающий колебательный характер, нужно, чтобы 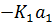 =0.Тогда корни характеристического уравнения будут иметь только мнимую часть.
=0.Тогда корни характеристического уравнения будут иметь только мнимую часть.  не может быть равно 0, следовательно,
не может быть равно 0, следовательно, 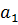 должно быть равно 0.
должно быть равно 0.

График переходных процессов с незатухающими колебаниями постоянной амплитуды и частоты.
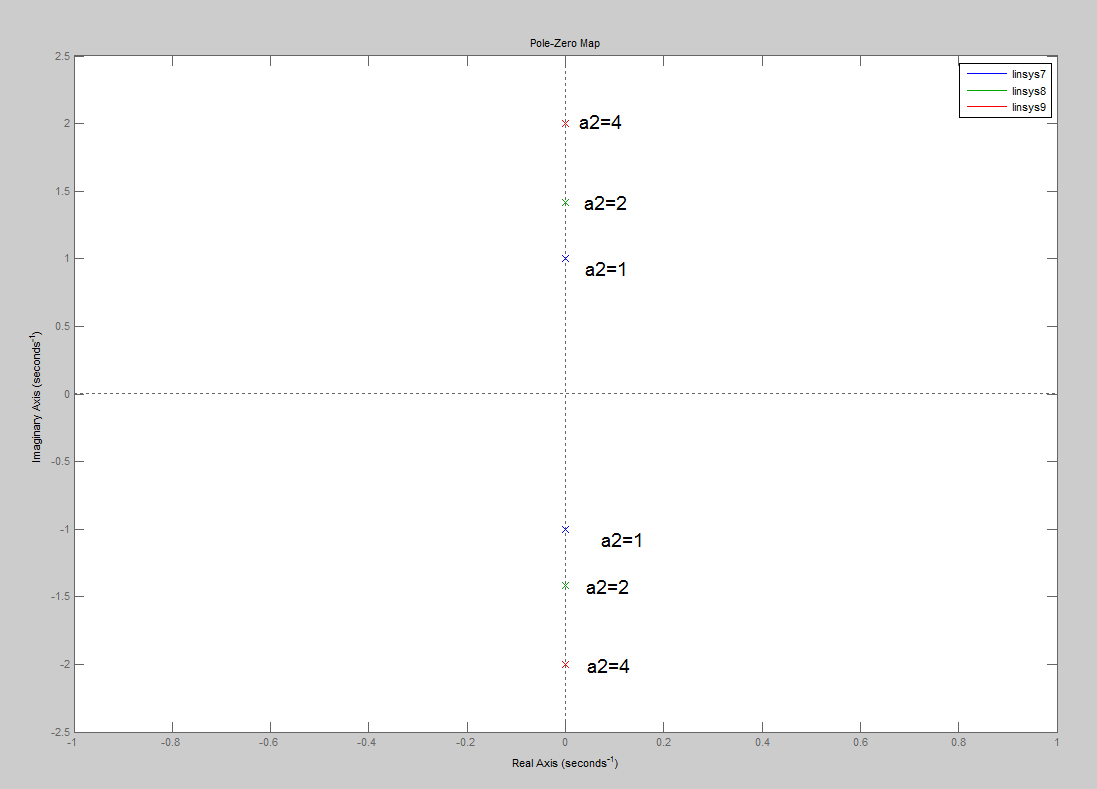
Корни характеристического уравнения при переходных процессах с незатухающими колебаниями постоянной частоты и амплитуды.

При коэффициенте 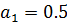 (диапазон
(диапазон 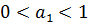 ) переходный процесс имеет сходящийся характер. Процесс устойчивый.
) переходный процесс имеет сходящийся характер. Процесс устойчивый.
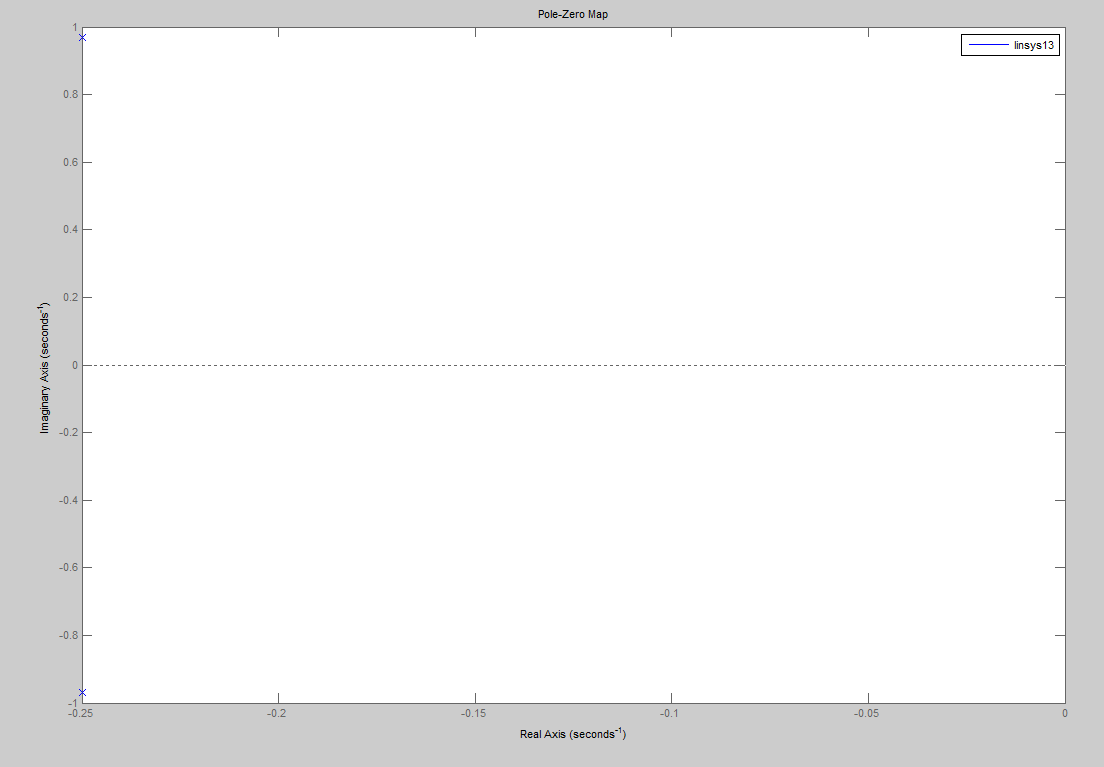
Корни характеристического уравнения при 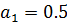 .
.
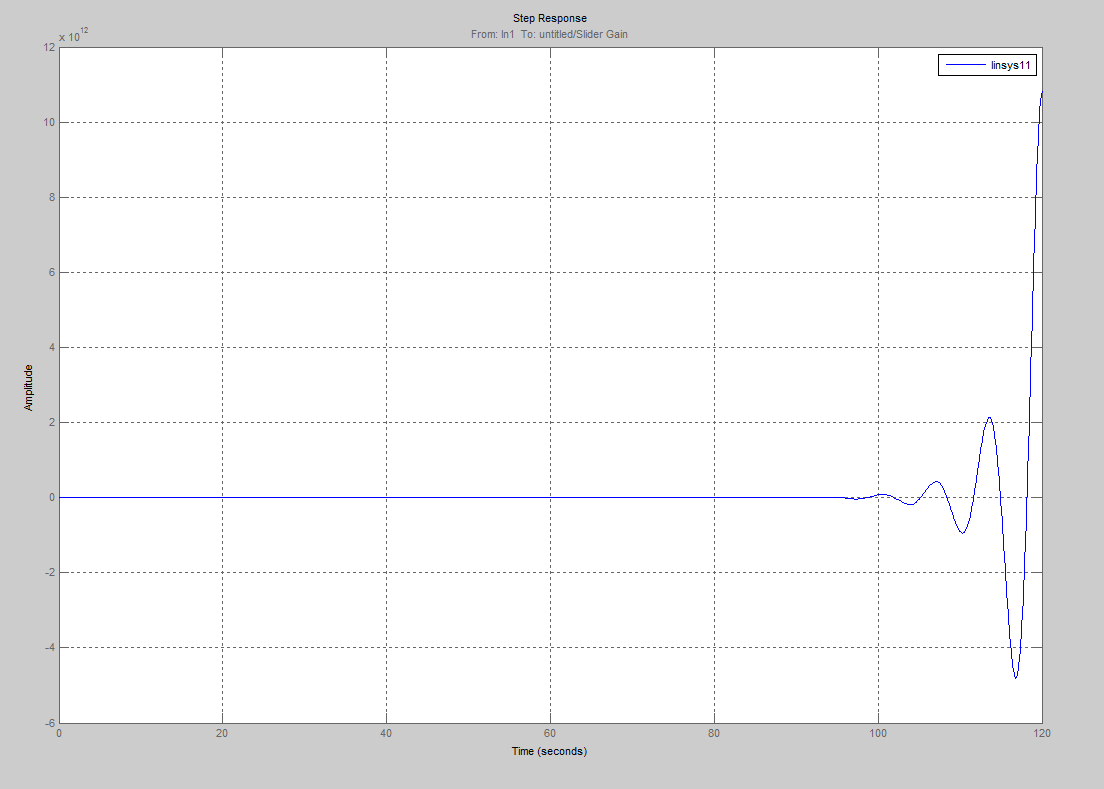
При коэффициенте 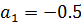 (диапазон
(диапазон 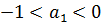 ) переходный процесс имеет расходящийся характер. Процесс неустойчивый.
) переходный процесс имеет расходящийся характер. Процесс неустойчивый.

Корни характеристического уравнения при 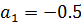 .
.
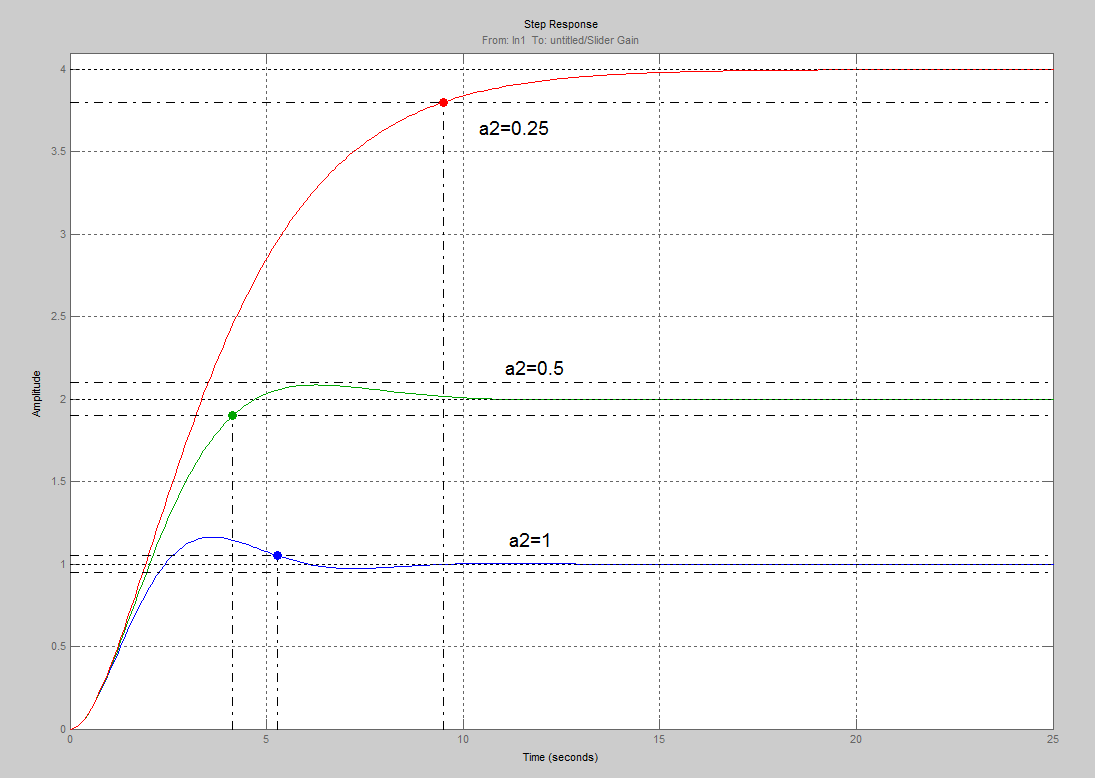
Графики переходных процессов при  .
.

Корни характеристического уравнения при  .
.
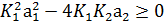 – условие для вещественных отрицательных корней
– условие для вещественных отрицательных корней
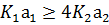
Следовательно, от 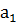 зависит характер переходного процесса (апериодический или колебательный).
зависит характер переходного процесса (апериодический или колебательный).
Вывод: При 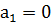 переходный процесс будет гармоническим,
переходный процесс будет гармоническим,  будет влиять на амплитуду колебаний. При
будет влиять на амплитуду колебаний. При 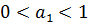 переходный процесс имеет сходящийся характер. Процесс устойчивый. При
переходный процесс имеет сходящийся характер. Процесс устойчивый. При  переходный процесс имеет расходящийся характер. Процесс неустойчивый. От коэффициента
переходный процесс имеет расходящийся характер. Процесс неустойчивый. От коэффициента  зависят характер переходного процесса, апериодический
зависят характер переходного процесса, апериодический
(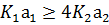 ) или колебательный (
) или колебательный (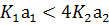 ) и амплитуда выходного сигнала (обратная зависимость).
) и амплитуда выходного сигнала (обратная зависимость).