Закон больших чисел - это
—действия над большими числами
—правила выполнения арифметических действий над большими
числами
—закон распределения большого числа случайных величин
+ группа теорем о средних характеристиках случайных величин
при большом числе испытаний
Последовательность случайных величин X1,X2,...,Xn,... называется
сходящейся по вероятности при  к случайной величине Х, если при любом сколь угодно малом
к случайной величине Х, если при любом сколь угодно малом  > 0
> 0
 —
—
—
+
—
Лемма Маркова оценивает вероятность того, что положительная
случайная величина Х не превзойдет
—ее дисперсии
—ее среднего квадратического отклонения
—предельной ошибки
+ t2 - кратного математического ожидания
Из обобщенной теоремы Чебышева следует, что если дисперсии
попарно независимых случайных величин ограничены сверху
константой C > 0, то
—средняя арифметическая случайных величин равна средней
арифметической их математических ожиданий
—средняя арифметическая случайных величин равна
математическому ожиданию одной из них
—средняя арифметическая случайных величин больше средней
арифметической их математических ожиданий
+ средняя арифметическая случайных величин сходится по
вероятности к среднему арифметическому их математических
ожиданий
Из обобщенной теоремы Чебышева следует, что 
+ равна 1
—равна 0
—больше, чем 
—равна 
Неравенство Чебышева оценивает вероятность того, что
отклонение случайной величины Х от ее математического
ожидания
—положительно
—отрицательно
+ по абсолютной величине не превзойдет определенного
положительного числа а
—по абсолютной величине превзойдет определенное
положительное число а
Из неравенства Чебышева с вероятностью, большей, чем 
можно утверждать, что абсолютная величина отклонения случайной величины Х от ее математического ожидания
—больше, чем а > 0
+ не превзойдет а > 0
—равна а > 0
—равна 0
Оценочное неравенство обобщенной теоремы Чебышева
оценивает вероятность того, что
+ абсолютная величина отклонения среднего арифметического случайных величин от среднего арифметического их математических ожиданий не превзойдет 
 —сумма случайных величин не превзойдет
—сумма случайных величин не превзойдет
 —разность случайных величин не превзойдет
—разность случайных величин не превзойдет
—отклонение суммы случайных величин от суммы их математических ожиданий не превзойдет 
При неограниченном увеличении числа независимых испытаний с одинаковой вероятностью появления события А в каждом испытании
—относительная частота события А равна вероятности этого
события
+ относительная частота события А сходится по вероятности к
вероятности этого события
—относительная частота события А больше вероятности этого
события
—относительная частота события А меньше, чем s > 0
Закон больших чисел является теоретическим обоснованием
+ выборочного метода
—статистической проверки гипотез
—интегральной теоремы Лапласа
—формул комбинаторики
Закон больших чисел гласит, что средняя арифметическая значений большого числа случайных величин
—является случайной величиной
+ стремится к постоянному числу
—стремится к случайной величине, имеющей показательное
распределение
—стремится к случайной величине, имеющей биномиальное
распределение
Центральная предельная теорема устанавливает условия, при которых сумма случайных величин имеет распределение, близкое
—к показательному распределению
—к равномерному распределению
—к биномиальному распределению
+ к нормальному распределению
Из закона больших чисел следует, что на среднем результате воздействия большого числа явлений воздействие одного из этих явлений
—не сказывается
—сильно сказывается
+ мало сказывается
—является преобладающим
Лемма Маркова утверждает, что положительная случайная величина не превосходит t2 кратного математического ожидания свероятностью, большей
—1/2
—1/t
—1/t2
+ 1-1/t2
Неравенство Чебышева утверждает, что вероятность отклонения случайной величины Х от ее математического ожидания на величину а больше, чем

—
—
—
+
Из теоремы Бернулли следует, что 
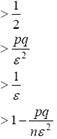
—
—
—
+
В теореме Пуассона, входящей в закон больших чисел, 

—
—
—
 +
+

Из
В теореме Пуассона, входящей в закон больших чисел, 
—
—
—
+
Из теоремы Пуассона следует, что 

—
—
—
+
Обобщенная теорема Чебышева утверждает, что для случайных величин, дисперсии которых ограничены сверху постоянным числом С, выполняется неравенство 
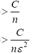
—
—
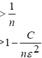
—
+
В трактовке теоремы Чебышева, называемой «Законом больших чисел», утверждается, что 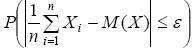
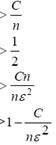
—
—
—
+
Для выполнения центральной предельной теоремы Ляпунова
обязательно условие
—число случайных величин ограничено
—случайные величины имеют показательное распределение
—случайные величины распределены АО показательному закону
+ число случайных величин неограниченно увеличиваются
Для выполнения центральной предельной теоремы Ляпунова
обязательно условие
—случайные величины распределены равномерно
—случайные величины имеют показательное распределение
+ случайные величины независимы
—число случайных величин конечно
Для выполнения центральной предельной теоремы Ляпунова
обязательно условие
—случайные величины распределены равномерно
—случайные величины распределены нормально
+ случайные величины имеют конечные математические
ожидания и дисперсии
—случайные величины имеют биномиальное распределение
Для выполнения центральной предельной теоремы Ляпунова
обязательно условие
—случайные величины имеют биномиальное распределение
—случайные величины распределены равномерно
—число случайных величин конечно
+ ни одна из случайных величин не выделяется по своему
действию на сумму
Из Леммы Маркова следует, что 

—
—
—
+
В группу теорем закона больших чисел не входит
—теорема Бернулли
—теорема Пуассона
—обобщенная теорема Чебышева
+ теорема Лапласа
В группу теорем закона больших чисел не входит
—теорема Бернулли
—теорема Пуассона
—неравенство Чебышева
+ теорема Коши
В группу теорем закона больших чисел не входит
—неравенство Чебышева
—теорема Бернулли
—теорема Пуассона
 + теорема Лагранжа
+ теорема Лагранжа
В неравенстве Чебышева
 —
—
—
—

+
В предельной форме теорема Пуассона утверждает, что
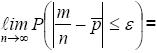
—0
—1/2
—const
+ 1
Предельная форма обобщенной теоремы Чебышева утверждает, что

—0
—1/2
— 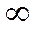
+ 1
В теореме Пуассона 
—средняя геометрическая
—средняя интегральная
+ средняя арифметическая взвешенная
—произвольная
Обобщенная теорема Чебышева выполняется для случайных
величин, для которых
—математические ожидания ограничены сверху
—вероятности наступления малы
—сумма вероятностей больше единицы
+ исперсии ограничены сверху некоторым постоянным числом
В теореме Пуассона 
—вероятностью наступления события А
—вероятностью не наступления события А
+ относительной частотой события А
—вероятностью достоверного события
Математическое ожидание случайной величины Х равно 3,2.
Вероятность того, что Х не превзойдет 4,0, больше, чем
+ 0,20
—0,16
—0,43
—0,31
Дисперсия случайной величины Х равна 0,15. Наибольшее
отклонение случайной величины Х от ее математического
ожидания М(Х) по абсолютной величине с вероятностью большей,
чем 0,5, равно
—0,31
+ 0,55
—0,16
—0,49
Вероятность наступления события А равна 0,6. Проведено 500
независимых испытаний. Вероятность того, что абсолютная
величина отклонения случайной величины Х - числа наступлений
события от математического ожидания М(Х) не превзойдет 20,
больше, чем
—0,5
—0,6
+ 0,7
—0,8
Дисперсия случайной величины Х равна 0,6. Вероятность того, что абсолютная величина отклонения случайной величины Х от ее математического ожидания не превзойдет 1,2, больше, чем
—0,387
—0,222
+ 0,583
—0,838
Вероятность наступления события А в каждом испытании равна 0,4. Проводится 200 испытаний. Вероятность того, что число наступлений события отклонится от его математического ожидания по абсолютной величине не более, чем на 16, больше, чем
—0,667
+ 0,813
—0,765
—0,973
Дисперсия каждой из 2000 случайных величин не превышает 9. Вероятность того, что отклонение средней арифметической этих величин от средней арифметической их математических
ожиданий по абсолютной величине не превышает 0,1, больше, чем
—0,45
+ 0,55
—0,65
—0,75
Вероятность того, что отклонение случайной величины Х от М(Х) по абсолютной величине не превзойдет 0,5, больше, чем 0,4. Дисперсия D(X) равна
+ 0,1
—0,15 —0,25 —0,3
Вероятность того, что случайная величины Х не превзойдет 6, больше, чем 0,75. Математическое ожидание М(Х) равно
—0,5
— 1
+ 1,5
—2
Математическое ожидание случайной величины Х М(Х)=3. Вероятность того, что случайная величины Х не превзойдет a, больше, чем 0,6. Значение a равно
— 1,8
—5
—3,6
+ 7,5
Случайная величина Х - число наступлений события А в n независимых испытаниях с вероятностью наступления события А в каждом испытании p=0,3. Вероятность того, что абсолютная величина отклонения Х от М(Х) не превзойдет 5, больше, чем 0,16. Число n равно
+ 100
—200
— 150
—50
Вероятность того, что абсолютная величина отклонения относительной частоты m/n наступления события в n независимых испытаниях от вероятности этого события p=0,25 не превзойдет 0,05, больше, чем 0,7. Число n равно
— 100
— 150
—200
+ 250
Дисперсия каждой из n случайных величин не превышает 6. Вероятность того, что отклонение средней арифметической этих величин от средней арифметической их математических ожиданий по абсолютной величине не превзойдет 0,1, больше, чем 0,5. Число n равно
— 1000
+ 1200
— 1400
— 1600
—
Случайная величина Х - число наступлений события А в 200 независимых испытаниях с одинаковой вероятностью p=0,2 события А в каждом испытании. Вероятность того, что Х не превзойдет 80, больше
—0,3
—0,4
—0,5
+ 0,6
Вероятность того, что положительная случайная величины Х не превзойдет t2 -кратного математического ожидания, больше, чем 5/9. Число t равно
—1/2
+ 3/2
—5/2
—7/2
Тема 8. Выборочный метод
Если генеральная совокупность неоднородна, то способ отбора
—серийный
—собственно - случайный
+ типический
—механический
Статистическое распределение выборки - это
+ соответствие между вариационным и частотным рядами
—вариационный ряд
—частотный ряд
—число вариант в вариационном ряду
Мерой колеблемости признака около среднего значения в выборочной совокупности является
—предельная ошибка выборки
—выборочная доля
—коэффициент надежности
+ выборочная дисперсия
Ошибкой репрезентативности (выборки) называется
—ошибка при вычислении характеристик выборочной совокупности
+ отклонение характеристик выборочной совокупности от соответствующих характеристик генеральной совокупности
—ошибка при вычислении характеристик генеральной совокупности
—среднее квадратическое отклонение
Надежностью оценки числовой характеристики генеральной совокупности называется
+ вероятность попадания этой характеристики в доверительный интервал
—отношение предельной ошибки выборки к средней ошибке
—доверительный интервал
—точность оценки
В выборочном методе гистограмма - это графическая иллюстрация
—функции распределения
—функции распределения
—плотности распределения
+ статистического распределения выборки при интервальном задании вариационного ряда
—закона распределения дискретной случайной величины
К числовым характеристикам выборочной совокупности относится
—предельная ошибка выборки
—генеральная доля
—коэффициент надежности
+ выборочная доля
Средняя ошибка выборки - это
—выборочная средняя
—выборочное среднее квадратическое отклонение
+ среднее отклонение характеристики выборочной совокупности от соответствующей характеристики генеральной совокупности
—выборочная дисперсия
Доверительный интервал - это интервал, в который с надежностью у попадает
+ характеристика генеральной совокупности
—характеристика выборочной совокупности
—значение изучаемого признака генеральной совокупности
—значение изучаемого признака выборочной совокупности
Выборочная средняя - это
—значение изучаемого признака, выбранное из середины вариационного ряда
+ среднее взвешенное значение признака в выборочной совокупности
―среднее арифметическое всех значений признака в выборочной совокупности
—среднее взвешенное квадратов отклонений значений признака около среднего
Выборочная средняя равна
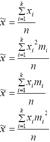 -
-
-
+
-
Величина объема выборки зависит от
+ требуемой точности и надежности результатов
—генеральной дисперсии
—выборочной средней
—генеральной средней
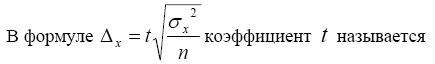
—коэффициентом выборки
+ коэффициентом надежности
—признаком выборки
—точностью оценки
При повторном собственно - случайном отборе предельная ошибка выборки зависит от
—объема генеральной совокупности
—генеральной дисперсии
+ объема выборочной совокупности
—выборочной средней
При серийном отборе под объемом выборки понимается
—среднее количество элементов в серии
―количество элементов в одной из серий
—наибольшее количество элементов во всех сериях
+ количество серий, выбранных из общего количества серий
Выборочный метод опирается на
—теорему Бернулли
―теорему Пуаcсона
—лемму Маркова
+ теорему Чебышева -Ляпунова
При повторном отборе зарегистрированные и обследованные единицы
+ вновь возвращаются в генеральную совокупность и снова могут принять участие в дальнейшем отборе
—в генеральную совокупность не возвращаются
—в генеральную совокупность возвращаются, но принять участие в дальнейшем отборе не могут
—помечаются специальным знаком
При бесповторном отборе зарегистрированные и обследованные единицы
—возвращаются в генеральную совокупность
+ не возвращаются в генеральную совокупность
—возвращаются в генеральную совокупность и могут принять участие в дальнейшем отборе
—либо возвращаются, либо не возвращаются в генеральную совокупность
При серийном способе отбора внутри выбранной серии проводится
+ сплошное наблюдение
—выборочное наблюдение
—наблюдение первых n элементов
—наблюдение последних n элементов
Типический способ отбора применяется в тех случаях, когда генеральная совокупность
—состоит из малого числа элементов
+ неоднородна
―однородна
—неупорядочена
К способам отбора, не требующим разделения на группы, относятся
—случайный и типический способы отбора
—типический и серийным способы отбора
—механический и серийный способы отбора
+ случайный и механический способы отбора
К способам отбора требующим разделения на группы, относятся
—случайный и типический способы отбора
+ типический и серийным способы отбора
—механический и серийный способы отбора
—случайный и механический способы отбора
Одной из основных задач выборочного метода является
—сплошное наблюдение
+ определение необходимой численности выборки
—подсчет количества элементов генеральной совокупности
―изучение изменчивости элементов генеральной совокупности
Выборочная дисперсия по средней - это
—среднее взвешенное значение квадратов признаков в выборке
+ среднее взвешенное квадратов отклонений значений признака около выборочной средней
—среднее значение признака в выборке
—наибольшее значение признака
Выборочную (по средней) дисперсию можно вычислять по формуле
 -
-
+
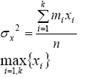
--
При типическом отборе численность каждого типа в выборке
—одинакова
—равна объему выборки
—обратно пропорциональна объему типа в генеральной совокупности
+ пропорциональна объему типа в генеральной совокупности
Частотный ряд это
—совокупность выборочных значений признака
—совокупность квадратов выборочных значений признака
+ упорядоченная последовательность частоты появлений различных значений признака
—соответствие между значениями признака и числом появления этих значений


—
+
—
—
Предельная ошибка ∆х показывает
—наименьшее отклонение выборочной средней от генеральной средней
—среднее отклонение выборочной средней от генеральной средней
+ наибольшее отклонение выборочной средней от генеральной средней
—наибольшую дисперсию
Упорядоченная последовательность вариант называется
—частотным рядом
—числовым рядом
+ вариационным рядом
—функциональным рядом
В выборочном методе полигон частот - это графическая иллюстрация
—функции распределения
???+ плотности распределения
—статистического распределения выборки при интервальном задании вариационного ряда
???—статистического распределения выборки при задании вариационного ряда в виде последовательности вариант
При возрастании объема выборки n предельная ошибка выборки
+ уменьшается
—увеличивается
—не изменяется
—стремится к бесконечности
При увеличении надежности  предельная ошибка выборки
предельная ошибка выборки
—уменьшается
+ увеличивается
—не изменяется
—стремится к 0
С вероятностью  можно утверждать, что при достаточно большом объеме выборки разница между
можно утверждать, что при достаточно большом объеме выборки разница между 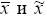 не превзойдет
не превзойдет
—коэффициента надежности t
—средней ошибки выборки
—дисперсии 
+ предельной ошибки выборки 
Величина объема выборки n зависит от
+ требуемых точности и надежности результатов
—изучаемого признака
—генеральной средней
—генеральной доли
При выборочном обследовании 100 единиц совокупности, полученной собственно - случайным способом, были получены следующие данные:
| x | 10-20 | 20-30 | 30-40 | 40-50 |
| m |
Выборочная средняя равна
—28
—29
—30
+ 31
При выборочном обследовании 100 единиц найдено среднее квадратическое отклонение  = 0,2. С вероятностью, равной 0,9973, предельная ошибка выборки по средней
= 0,2. С вероятностью, равной 0,9973, предельная ошибка выборки по средней  при повторном отборе равна
при повторном отборе равна
—0,2
—0,02
+ 0,06
—0,6
При выборочном обследовании стажа работы 100 сотрудников учреждения собственно - случайным способом отбора получены данные:
| x | 0-10 | 10-20 | 20-30 | 30-40 |
| m |
Доля сотрудников, имеющих стаж работы 20 лет и более, равна
—0,2
+ 0,4
—0,3
—0,1
Доля стандартных деталей в выборочной совокупности объемом в 100 штук, полученной путем повторного, собственно - случайного отбора, равна 0,8. С вероятностью 0,9973 предельная ошибка выборки по доле  w равна
w равна
—0,08
+ 0,12
—0,8
—1,2
При выборочном обследовании 80 единиц совокупности, полученной путем собственно - случайного отбора, были получены следующие данные:
| x | 5-15 | 15-25 | 25-35 | 35-45 |
| m |
Выборочная средняя равна
—28,6
—26,6
+ 25,6
—23,6
При выборочном обследовании 100 единиц совокупности собственно -случайным способом были получены следующие данные:
| x | 5-15 | 15-25 | 25-35 | 35-45 |
| m |
Выборочная средняя равна
+ 26
—28
—24
—27
 —0,1
—0,1
—0,2
—0,3
+ 0,4

—16
+ 64
 —256
—256
—128
—2
—3
+ 2,5
—3,5
 —
—
0,2
—0,4
 + 0,6
+ 0,6
—0,8
—450
 + 4500
+ 4500
—150
—1500
+ 24
—3
—0,24
—0,72
При выборочном обследовании некоторой совокупности, полученной собственно - случайным способом, были получены следующие данные:
| x | 2-4 | 4-6 | 6-8 | 8-10 |
| m |
Выборочная средняя равна
+ 6,1
—12,2
—3,05
—8,3
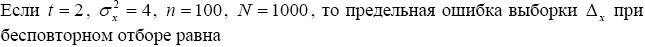
—0,4
+ 0,38
—0,28
—0,45
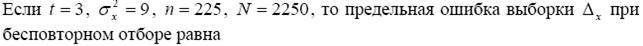 —0,36
—0,36
—0,72
+ 0,57
Тема 9. Статистическая проверка гипотез
При статистической проверке гипотез уровнем значимости а
называется
—вероятность допустить ошибку 1 - ого рода, т.е. принять
правильную нулевую гипотезу
+ вероятность допустить ошибку 1 - ого рода, т.е. отвергнуть
правильную нулевую гипотезу
—вероятность допустить ошибку 2 - ого рода, т.е. отвергнуть
правильную нулевую гипотезу
—вероятность допустить ошибку 2 - ого рода, т.е. принять
неправильную нулевую гипотезу
Критической областью называется
—множество значений критерия, где H0 принимается
+ множество значений критерия, при которых H0 отвергается
—область, в которой Kнаб = Kкр
—область, в которой Kнаб = 0
Тип (вид) критической области определяется
—уровнем значимости а
—знаком в нулевой гипотезе
—знаком Kнаб
+ знаком неравенства в альтернативной гипотезе
По данным выборки 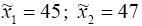 . При проверке гипотезы о
. При проверке гипотезы о
равенстве генеральных средних в конкурирующей гипотезе
должен быть знак
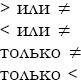 —
—
+
—
—
Статистические гипотезы
—выдвигаются о выборочных совокупностях, а проверяются по
генеральным совокупностям
—выдвигаются о выборочных совокупностях, а проверяются тоже
по выборочным совокупностям
+ выдвигаются о генеральных совокупностях, а проверяются по
выборочным совокупностям
—выдвигаются о генеральных совокупностях, а проверяются тоже
по генеральным совокупностям
Проверяемая гипотеза обозначается
+ Н0
—H2
—H1
—H3
Множество всех значений критерия, при которых H0 отвергается,
называется
—областью определения
—областью принятия гипотезы
+ критической областью
—областью существования
Форма критической области (левая, правая, двусторонняя) зависит
от
—гипотезы H0
+ гипотезы H1
—сочетания H0 и H1
—гипотезы H2
При статистической проверке гипотез критические точки это
—множество точек, образующих область принятия H0
—множество точек, образующих область принятия H1
+ точки, разделяющие область принятия гипотезы H0 и область
отвергания H0
—область существования H0
Гипотеза H0 принимается, если наблюдаемое значение критерия
—лежит в критической области
+ лежит в области принятия гипотезы
—лежит в области существования
—лежит на границе критической области и области принятия
гипотезы
Гипотеза H0 отвергается, если наблюдаемое значение критерия
+ лежит в критической области
—лежит в области принятия гипотезы
—лежит в области существования
—лежит на границе критической области
При статистической проверке гипотез наблюдаемое значение критерия Kнаб
—определяется из таблиц
+ вычисляется по исходным данным
—дается в условиях задачи
—не используется
При статистической проверке гипотез критическое значение критерия Kкр
+ определяется из таблиц
—вычисляется по исходным данным
—дается в условиях задачи
—не используется
При статистической проверке гипотез критерием называется
—константа, которая находится из условий задачи
—любая случайная величина
+ случайная величина с известным распределением
—константа, которая находится из таблиц
По данным выборки  . При проверке гипотезы о
. При проверке гипотезы о
равенстве генеральных средних в конкурирующей гипотезе
должен быть знак
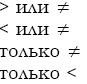 +
+
—
—
—
По данным выборки  . При проверке гипотезы о равенстве
. При проверке гипотезы о равенстве
генеральной средней стандарту(гипотетической средней) в
конкурирующей гипотезе должен быть знак
 —
—
+
—
—
По данным выборки  . При проверке гипотезы о равенстве генеральной средней стандарту(гипотетической средней) в конкурирующей гипотезе должен быть знак
. При проверке гипотезы о равенстве генеральной средней стандарту(гипотетической средней) в конкурирующей гипотезе должен быть знак
 +
+
—
—
—
При проверке гипотезы о равенстве генеральных дисперсий в
качестве критерия используется случайная величина, имеющая
распределение
+ Фишера - Снедекора (F)
—Стьюдента (T)
—нормальное (Z)
—Пирсона (X 2)
При проверке гипотезы о равенстве генеральных средних (малые выборки n1,n2 <30) используется случайная величина, имеющая
распределение
—Фишера - Снедекора (F)
+ Стьюдента (T)
—нормальное (Z)
—Пирсона (X2)
При проверке гипотезы о равенстве генеральных средних(большие выборки n1,n2 >30) используется случайная величина, имеющая
распределение
—Фишера - Снедекора (F)
—Стьюдента (T)
+ нормальное (Z)
—Пирсона (X2)
Альтернативная (конкурирующая) обозначается
-—H0
—H2
—H3
+ H1
Стандартный размер a = 42. По данным выборки размер 
 . При проверке гипотезы о равенстве генеральной средней стандарту в конкурирующей гипотезе должен быть знак
. При проверке гипотезы о равенстве генеральной средней стандарту в конкурирующей гипотезе должен быть знак
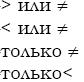 —
—
+
—
—
Уровень значимости определяет
—тип критической области
+ значение Kкр
—формулировку нулевой гипотезы
—формулировку конкурирующей гипотезы
Конкурирующая гипотеза определяет
+ тип критической области
—размер критической области
—распределение случайной величины, используемой в качестве
критерия при проверке гипотезы
—область принятия гипотезы
Если принимается гипотеза H1:D2>D1 о работе двух станков, то + первый станок налажен лучше
—второй станок налажен лучше
—станки налажены одинаково
—нельзя сделать вывода
К непараметрическим относятся гипотезы
—о равенстве генеральных средних
—о равестве генеральных дисперсий
+ о законах распределения
—об уровне значимости
Если конкурирующая гипотеза имеет вид  , то критическая область
, то критическая область
+ правосторонняя
—левосторонняя
—двусторонняя
—любая
РРРРH
Если конкурирующая гипотеза имеет вид  , то критическая область
, то критическая область
—правосторонняя
+ левосторонняя
—двусторонняя
—любая
Если конкурирующая гипотеза имеет вид  , то критическая область
, то критическая область
—правосторонняя
—левосторонняя
+ двусторонняя
—любая
Если конкурирующая гипотеза имеет вид H1: D1 # D2, то критическая область
+ двусторонняя
—левосторонняя
—любая
—правосторонняя
Двусторонняя критическая область соответствует гипотезе H1
вида
 —
—
—
+
—
Если принимается гипотеза H0:D1 = D2 о работе двух станков, то
—первый станок налажен лучше
—второй налажен лучше
—станки налажены неодинаково
+ станки налажены одинаковы
Если принимается гипотеза  о весе детали, то
о весе детали, то
+ вес детали соответствует стандарту
—тяжелее стандарта
—легче стандарта
—нельзя сделать вывода
 Малые выборки —
Малые выборки —
—
—
+
—
 Большие выборки
Большие выборки
—
+
—
—
При статистической проверке гипотезы о равенстве генеральных дисперсий в качестве критерия используется случайная величина, имеющая распределение
—Стьюдента (Т)
+ Фишера - Снедекора (F)
—нормальное (Z)
—Пирсона
При статистической проверке гипотезы о равенстве генеральных средних, в случае, когда генеральные дисперсии известны, используется случайная величина, имеющая распределение
—Фишера - Снедекора (F)
+ нормальное (Z)
—Стью дента (Т)
—Пирсона
При статистической проверке гипотезы о равенстве генеральной средней стандарту (генеральная дисперсия неизвестна) в качестве критерия используется случайная величина, имеющая распределение
+ Стьюдента (Т)
—нормальное (Z)
—Фишера - Снедекора (F)
—Пирсона
При статистической проверке гипотезы о равенстве генеральной средней стандарту (генеральная дисперсия известна) в качестве критерия используется случайная величина, имеющая распределение
+ нормальное (Z)
—Фишера - Снедекора (F)
—Пирсона
—Стьюдента (Т)
При статистической проверке гипотезы о равенстве генеральных средних (генеральные дисперсии неизвестны, но равны) в качестве критерия используется случайная величина, имеющая распределение
—Пирсона
—нормальное (Z)
+ Стьюдента (Т)
—Фишера - Снедекора (F)
Правильная форма нулевой гипотезы H0 имеет вид
 —
—
—
+
—
Альтернативная гипотеза имеет вид H1: x1 <x2. Критическая область -
—правосторонняя
—произвольная
+ левосторонняя
—двусторонняя
Границей между критической областью и областью принятия
нулевой гипотезы является
—прямая
—окружность
+ точка
—парабола
По данным выборки  . При проверке гипотезы о
. При проверке гипотезы о
равенстве генеральных средних в конкурирующей гипотезе должен быть знак
 +
+
—
—
—
Альтернативная гипотеза имеет вид  . Критическая область
. Критическая область
—правосторонняя
+ двусторонняя
—произвольная
—левосторонняя
Исправленная