ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ
МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ЭКОНОМИКИ, СТАТИСТИКИ И ИНФОРМАТИКИ
Семестровая работа по курсу
«Диагностика кризисного состояния предприятия»
Выполнила: Чумарина Диляра Равилевна
Группа: ДЭС-401
Проверил: д.т.н., профессор
Фомин Ярослав Алексеевич
Москва, 2010
Введение.
В данной работе производится дискриминация России по обучающей выборке стран Европы, которые предварительно разделены на 2 группы: передовые страны и отстающие страны. За основу дискриминации взяты несколько основных показателей экономического развития страны. Для первоначального разбиения использовался показатель «ВВП на душу населения, тыс. евро».
Кроме того, проводится сравнение уровня развития России и других стран бывшего советского лагеря в динамике за 2004-2007 годы.
Исходные данные.
| Признак | ||||
| Передовые страны S1 | ||||
| X1(1) | X2(1) | X3(1) | X4(1) | |
| ВВП на душу населения, тыс.евро | 60,307 | 34,631 | 25,838 | 41,575 |
| Кол-во автомобилей на 1 тыс.чел. | ||||
| Средняя продолжительность жизни мужчин, лет (ожидаемая) |
X1(1) – Норвегия
X2(1) – Нидерланды
X3(1) – Италия
X4(1) – Швейцария
| Признак | Отстающие страны S2 | |||
| X1(1) | X2(1) | X3(1) | X4(1) | |
| ВВП на душу населения, тыс.евро | 5,547 | 8,411 | 10,067 | 15,409 |
| Кол-во автомобилей на 1 тыс.чел. | ||||
| Средняя продолжительность жизни мужчин, лет (ожидаемая) |
X1(1) – Румыния
X2(1) – Литва
X3(1) – Венгрия
X4(1) – Португалия
Обучение с тремя показателями.
1. Для групп стран S1 и S2 составим векторы средних (соответственно а1 и а2), а также их разность.
| 40,59 | 9,76 | 50,35 | 30,83 | ||||
| а1= | 488,25 | а2= | 346,25 | а1+а2= | 834,5 | а1-а2= | |
| 77,25 | 68,5 | 145,75 | 8,75 |
2. Вычислим ковариационные матрицы М1 и М2, где m1 и m2 количество преуспевающих и кризисных предприятий соответственно
2.1. Ковариационная матрица М1

| 19,71925 | ||||||
| (X1(1)-a1)= | -59,25 | (X1(1)-a1)T= | 19,71925 | -59,25 | 0,75 | |
| 0,75 | ||||||
| -5,95675 | ||||||
| (X2(1)-a1)= | -59,25 | (X2(1)-a1)T= | -5,95675 | -59,25 | -1,25 | |
| -1,25 | ||||||
| -14,7498 | ||||||
| (X3(1)-a1)= | 92,75 | (X3(1)-a1)T= | -14,7498 | 92,75 | -0,25 | |
| -0,25 | ||||||
| 0,98725 | ||||||
| (X4(1)-a1)= | 25,75 | (X4(1)-a1)T= | 0,98725 | 25,75 | 0,75 | |
| 0,75 |
| 388,8488 | -1168,37 | 14,78944 | |
| (X1(1)-a1)(X1(1)-a1)T = | -1168,37 | 3510,563 | -44,4375 |
| 14,78944 | -44,4375 | 0,5625 | |
| 35,48287 | 352,9374 | 7,445938 | |
| (X2(1)-a1)(X2(1)-a1)T = | 352,9374 | 3510,563 | 74,0625 |
| 7,445938 | 74,0625 | 1,5625 | |
| 217,5551 | -1368,04 | 3,687438 | |
| (X3(1)-a1)(X3(1)-a1)T = | -1368,04 | 8602,563 | -23,1875 |
| 3,687438 | -23,1875 | 0,0625 | |
| 0,974663 | 25,42169 | 0,740438 | |
| (X4(1)-a1)(X4(1)-a1)T = | 25,42169 | 663,0625 | 19,3125 |
| 0,740438 | 19,3125 | 0,5625 | |
| 642,8615 | -2158,05 | 26,66325 | |
 = =
| -2158,05 | 16286,75 | 25,75 |
| 26,66325 | 25,75 | 2,75 | |
| 214,2872 | -719,349 | 8,88775 | |
| М1 = | -719,349 | 5428,917 | 8,583333 |
| 8,88775 | 8,583333 | 0,916667 |
2.2. Ковариационная матрица М2
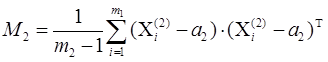
| -4,6115 | ||||||
| (X1(2)-a2)= | -197,25 | (X1(2)-a2)T= | -4,6115 | -197,25 | -1,5 | |
| -1,5 | ||||||
| -1,3475 | ||||||
| (X2(2)-a2)= | 37,75 | (X2(2)-a2)T= | -1,3475 | 37,75 | -2,5 | |
| -2,5 | ||||||
| 0,3085 | ||||||
| (X3(2)-a2)= | -66,25 | (X3(2)-a2)T= | 0,3085 | -66,25 | -0,5 | |
| -0,5 | ||||||
| 5,6505 | ||||||
| (X4(2)-a2)= | 225,75 | (X4(2)-a2)T= | 5,6505 | 225,75 | 4,5 | |
| 4,5 |
| 21,26593 | 909,6184 | 6,91725 | |
| (X1(2)-a2)(X1(2)-a2)T = | 909,6184 | 38907,56 | 295,875 |
| 6,91725 | 295,875 | 2,25 | |
| 1,815756 | -50,8681 | 3,36875 | |
| (X2(2)-a2)(X2(2)-a2)T = | -50,8681 | 1425,063 | -94,375 |
| 3,36875 | -94,375 | 6,25 | |
| 0,095172 | -20,4381 | -0,15425 | |
| (X3(2)-a2)(X3(1)-a2)T = | -20,4381 | 4389,063 | 33,125 |
| -0,15425 | 33,125 | 0,25 | |
| 31,92815 | 1275,6 | 25,42725 | |
| (X4(2)-a2)(X4(2)-a2)T = | 1275,6 | 50963,06 | 1015,875 |
| 25,42725 | 1015,875 | 20,25 | |
| 55,10501 | 2113,913 | 35,559 | |
 = =
| 2113,913 | 95684,75 | 1250,5 |
| 35,559 | 1250,5 | ||
| 18,36834 | 704,6375 | 11,853 | |
| М1 = | 704,6375 | 31894,92 | 416,8333 |
| 11,853 | 416,8333 | 9,666667 |
3. Найдём общую ковариационную матрицу М

| 155,1037 | -9,80739 | 13,82717 | |
| М = | -9,80739 | 24882,56 | 283,6111 |
| 13,82717 | 283,6111 | 7,055556 |
4. Найдём обратную матрицу М-1
| 0,00959 | 0,000402 | -0,03497 | |
| M-1 = | 0,000402 | 9,1E-05 | -0,00445 |
| -0,03497 | -0,00445 | 0,389067 |
5. Найдём произведение транспонированной разности векторов средних групп предприятий (а1-а2)Т и обратной общей ковариационной матрицы M-1
| (а1-а2)T = | 30,82925 | 8,75 | |
| 1/2*(а1-а2)T = | 15,41463 | 4,375 | |
| (а1-а2)T M-1 = | 0,046827 | -0,01359 | 1,694698 |
| 1/2 (а1-а2)T M-1 = | 0,023414 | -0,0068 | 0,847349 |
Для определения достоверности:
- Вычислим расстояние Махаланобиса:
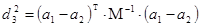
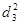 =14,342
=14,342
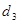 =3,787
=3,787
- Найдем
 и
и 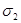

 0,707
0,707

 2,121
2,121
- Найдем
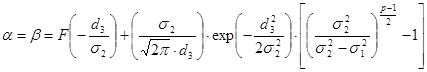
p=3
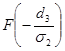 =0,03711
=0,03711
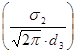 = 0,22346
= 0,22346
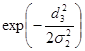 = 0,20319
= 0,20319
 = 1,125
= 1,125
 =0,08819
=0,08819
Достоверность прогноза равна  = 0,91181
= 0,91181
Обучение с четырьмя показателями.
Добавим ещё один показатель – производство электроэнергии на душу населения.
| Признак | Передовые страны S1 | |||
| X1(1) | X2(1) | X3(1) | X4(1) | |
| ВВП на душу населения, тыс.евро | 60,307 | 34,631 | 25,838 | 41,575 |
| Кол-во автомобилей на 1 тыс.чел. | ||||
| Средняя продолжительность жизни мужчин, лет (ожидаемая) | ||||
| Производство электроэнергии на душу населения, МВт/ч | 26,101 | 6,015 | 5,339 | 8,577 |
X1(1) – Норвегия
X2(1) – Нидерланды
X3(1) – Италия
X4(1) – Швейцария
| Признак | Отстающие страны S2 | |||
| X1(1) | X2(1) | X3(1) | X4(1) | |
| ВВП на душу населения, тыс.евро | 5,547 | 8,411 | 10,067 | 15,409 |
| Кол-во автомобилей на 1 тыс.чел. | ||||
| Средняя продолжительность жизни мужчин, лет (ожидаемая) | ||||
| Производство электроэнергии на душу населения, МВт/ч | 2,917 | 3,671 | 3,556 | 4,623 |
X1(1) – Румыния
X2(1) – Литва
X3(1) – Венгрия
X4(1) – Португалия
1. Для групп стран S1 и S2 составим векторы средних (соответственно а1 и а2), а также их разность.
| 40,58775 | 9,7585 | 50,34625 | 30,82925 | ||||
| а1= | 488,25 | а2= | 346,25 | а1+а2= | 834,5 | а1-а2= | |
| 77,25 | 68,5 | 145,75 | 8,75 | ||||
| 11,508 | 3,69175 | 15,19975 | 7,81625 |
2. Вычислим ковариационные матрицы М1 и М2, где m1 и m2 количество преуспевающих и кризисных предприятий соответственно
2.1. Ковариационная матрица М1

| 19,7192 | |||||||
| (X1(1)-a1)= | -59,25 | (X1(1)-a1)T= | 19,71925 | -59,25 | 0,75 | 14,593 | |
| 0,75 | |||||||
| 14,593 | |||||||
| -5,95675 | |||||||
| (X2(1)-a1)= | -59,25 | (X2(1)-a1)T= | -5,95675 | -59,25 | -1,25 | -5,493 | |
| -1,25 | |||||||
| -5,493 | |||||||
| -14,7498 | |||||||
| (X3(1)-a1)= | 92,75 | (X3(1)-a1)T= | -14,7498 | 92,75 | -0,25 | -6,169 | |
| -0,25 | |||||||
| -6,169 | |||||||
| 0,98725 | |||||||
| (X4(1)-a1)= | 25,75 | (X4(1)-a1)T= | 0,98725 | 25,75 | 0,75 | -2,931 | |
| 0,75 | |||||||
| -2,931 |
| 388,8488 | -1168,37 | 14,78944 | 287,763 | |
| (X1(1)-a1)(X1(1)-a1)T = | -1168,37 | 3510,563 | -44,4375 | -864,635 |
| 14,78944 | -44,4375 | 0,5625 | 10,94475 | |
| 287,763 | -864,635 | 10,94475 | 212,9556 | |
| 35,48287 | 352,9374 | 7,445938 | 32,72043 | |
| (X2(1)-a1)(X2(1)-a1)T = | 352,9374 | 3510,563 | 74,0625 | 325,4603 |
| 7,445938 | 74,0625 | 1,5625 | 6,86625 | |
| 32,72043 | 325,4603 | 6,86625 | 30,17305 | |
| 217,5551 | -1368,04 | 3,687438 | 90,99121 | |
| (X3(1)-a1)(X3(1)-a1)T = | -1368,04 | 8602,563 | -23,1875 | -572,175 |
| 3,687438 | -23,1875 | 0,0625 | 1,54225 | |
| 90,99121 | -572,175 | 1,54225 | 38,05656 | |
| 0,974663 | 25,42169 | 0,740438 | -2,89363 | |
| (X4(1)-a1)(X4(1)-a1)T = | 25,42169 | 663,0625 | 19,3125 | -75,4733 |
| 0,740438 | 19,3125 | 0,5625 | -2,19825 | |
| -2,89363 | -75,4733 | -2,19825 | 8,590761 | |
| 642,8615 | -2158,05 | 26,66325 | 408,581 | |
 = =
| -2158,05 | 16286,75 | 25,75 | -1186,82 |
| 26,66325 | 25,75 | 2,75 | 17,155 | |
| 408,581 | -1186,82 | 17,155 | 289,776 | |
| 214,2872 | -719,349 | 8,88775 | 136,1937 | |
| М1 = | -719,349 | 5428,917 | 8,583333 | -395,608 |
| 8,88775 | 8,583333 | 0,916667 | 5,718333 | |
| 136,1937 | -395,608 | 5,718333 | 96,59201 |
2.2. Ковариационная матрица М2
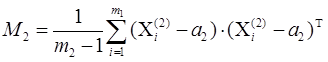
| -4,6115 | |||||||
| (X1(2)-a2)= | -197,25 | (X1(2)-a2)T= | -4,6115 | -197,25 | -1,5 | -0,77475 | |
| -1,5 | |||||||
| -0,77475 | |||||||
| -1,3475 | |||||||
| (X2(2)-a2)= | 37,75 | (X2(2)-a2)T= | -1,3475 | 37,75 | -2,5 | -0,02075 | |
| -2,5 | |||||||
| -0,02075 | |||||||
| 0,3085 | |||||||
| (X3(2)-a2)= | -66,25 | (X3(2)-a2)T= | 0,3085 | -66,25 | -0,5 | -0,13575 | |
| -0,5 | |||||||
| -0,13575 | |||||||
| 5,6505 | |||||||
| (X4(2)-a2)= | 225,75 | (X4(2)-a2)T= | 5,6505 | 225,75 | 4,5 | 0,93125 | |
| 4,5 | |||||||
| 0,93125 |
| 21,26593 | 909,6184 | 6,91725 | 3,57276 | |
| (X1(2)-a2)(X1(2)-a2)T = | 909,6184 | 38907,56 | 295,875 | 152,8194 |
| 6,91725 | 295,875 | 2,25 | 1,162125 | |
| 3,57276 | 152,8194 | 1,162125 | 0,600238 | |
| 1,815756 | -50,8681 | 3,36875 | 0,027961 | |
| (X2(2)-a2)(X2(2)-a2)T = | -50,8681 | 1425,063 | -94,375 | -0,78331 |
| 3,36875 | -94,375 | 6,25 | 0,051875 | |
| 0,027961 | -0,78331 | 0,051875 | 0,000431 | |
| 0,095172 | -20,4381 | -0,15425 | -0,04188 | |
| (X3(2)-a2)(X3(2)-a2)T = | -20,4381 | 4389,063 | 33,125 | 8,993437 |
| -0,15425 | 33,125 | 0,25 | 0,067875 | |
| -0,04188 | 8,993437 | 0,067875 | 0,018428 | |
| 31,92815 | 1275,6 | 25,42725 | 5,262028 | |
| (X4(2)-a2)(X4(2)-a2)T = | 1275,6 | 50963,06 | 1015,875 | 210,2297 |
| 25,42725 | 1015,875 | 20,25 | 4,190625 | |
| 5,262028 | 210,2297 | 4,190625 | 0,867227 | |
| 55,10501 | 2113,913 | 35,559 | 8,82087 | |
 = =
| 2113,913 | 95684,75 | 1250,5 | 371,2593 |
| 35,559 | 1250,5 | 5,4725 | ||
| 8,82087 | 371,2593 | 5,4725 | 1,486323 | |
| 18,36834 | 704,6375 | 11,853 | 2,94029 | |
| М2 = | 704,6375 | 31894,92 | 416,8333 | 123,7531 |
| 11,853 | 416,8333 | 9,666667 | 1,824167 | |
| 2,94029 | 123,7531 | 1,824167 | 0,495441 |
Найдём общую ковариационную матрицу М

| 155,1037 | -9,80739 | 13,82717 | 92,75598 | |
| -9,80739 | 24882,56 | 283,6111 | -181,236 | |
| М = | 13,82717 | 283,6111 | 7,055556 | 5,028333 |
| 92,75598 | -181,236 | 5,028333 | 64,72497 |
Найдём обратную матрицу М-1
| 0,064894 | 0,000268 | -0,07646 | -0,08631 | |
| 0,000268 | 9,14E-05 | -0,00435 | 0,000209 | |
| M-1 = | -0,07646 | -0,00435 | 0,420192 | 0,064748 |
| -0,08631 | 0,000209 | 0,064748 | 0,134689 |
Найдём произведение транспонированной разности векторов средних групп предприятий (а1-а2)Т и обратной общей ковариационной матрицы M-1
| (а1-а2)T = | 30,82925 | 8,75 | 7,81625 | |
| 1/2*(а1-а2)T = | 15,41463 | 4,375 | 3,908125 | |
| (а1-а2)T M-1 = | 0,695156 | -0,01516 | 1,208316 | -1,01178 |
| 1/2 (а1-а2)T M-1 = | 0,347578 | -0,00758 | 0,604158 | -0,50589 |